Hardball Retrospective – The “Original” 2003 Florida Marlins
In “Hardball Retrospective: Evaluating Scouting and Development Outcomes for the Modern-Era Franchises”, I placed every ballplayer in the modern era (from 1901-present) on their original team. Consequently, Reggie Jackson is listed on the Athletics roster for the duration of his career while the Mets claim Tom Seaver and the Cardinals declare Steve Carlton. I calculated revised standings for every season based entirely on the performance of each team’s “original” players. I discuss every team’s “original” players and seasons at length along with organizational performance with respect to the Amateur Draft (or First-Year Player Draft), amateur free agent signings and other methods of player acquisition. Season standings, WAR and Win Shares totals for the “original” teams are compared against the real-time or “actual” team results to assess each franchise’s scouting, development and general management skills.
Expanding on my research for the book, the following series of articles will reveal the finest single-season rosters for every Major League organization based on overall rankings in OWAR and OWS along with the general managers and scouting directors that constructed the teams. “Hardball Retrospective” is available in Kindle format on Amazon.com and ePub format on KoboBooks.com – other eBook formats coming soon. Additional information and a discussion forum are available at TuataraSoftware.com.
Terminology
OWAR – Wins Above Replacement for players on “original” teams
OWS – Win Shares for players on “original” teams
OPW% – Pythagorean Won-Loss record for the “original” teams
Assessment
The 2003 Florida Marlins OWAR: 43.8 OWS: 260 OPW%: .522
GM Dave Dombrowski acquired all of the talent on the finest “Original” Marlins roster in team history – the 2003 squad. Fourteen of the 27 players were signed as amateur free agents and twelve entered the organization via the Amateur Draft. Kevin Millar was the lone exception as he was purchased from the St. Paul Saints (Northern League) in 1993. Based on the revised standings the “Original” 2003 Marlins notched 85 victories and tied the Expos for second place in the National League East, two games behind the Braves.
Cuban right-hander Livan Hernandez (15-10, 3.20) fashioned a career-best WHIP of 1.209 while leading the National League in complete games (8) and innings pitched (233.1). Josh Beckett paced the staff with a 3.04 ERA in 23 starts. Claudio Vargas, Gary Knotts and Nate Robertson rounded out the rotation. Felix Heredia (5-3, 2.69) delivered the best ERA and WHIP (1.230) of his career as the featured left-hander in the bullpen.
| ROTATION | POS | WAR | WS |
| Livan Hernandez | SP | 6.33 | 21.08 |
| Josh Beckett | SP | 3.04 | 10.93 |
| Claudio Vargas | SP | 1.41 | 6.65 |
| Gary Knotts | SP | -1.05 | 0.73 |
| Nate Robertson | SP | 0.05 | 1.32 |
| BULLPEN | POS | WAR | WS |
| Felix Heredia | RP | 1.48 | 8.18 |
| Will Cunnane | RP | 0.46 | 3.16 |
| Michael Tejera | SW | 0.01 | 3.19 |
| Vic Darensbourg | RP | -0.36 | 0.26 |
| Jason Pearson | RP | -0.54 | 0 |
| Hector Almonte | RP | -0.75 | 0 |
| Brian Meadows | SP | -0.27 | 3.12 |
| Blaine Neal | RP | -0.95 | 0 |
| Kevin Olsen | RP | -1.13 | 0 |
The Marlins’ farm system yielded two first-rate shortstops, Edgar Renteria and Alex “Sea Bass” Gonzalez. Renteria (.330/13/100) topped the club in BA, hits, doubles (47), RBI and stolen bases (34) while earning his second Gold Glove Award and appearing in his third All-Star game. Gonzalez tallied 33 two-baggers and swatted 18 big-flies. Second-sacker Luis Castillo managed a .314 BA and collected the first of three consecutive Gold Glove Awards. Miguel Cabrera was recalled in mid-June to handle assignments at third base and left field. The 20 year-old sensation from Maracay, Venezuela drove in 62 runs and placed fifth in the 2003 NL Rookie of the Year balloting. Kevin Millar slugged a team-high 25 round-trippers and plated 96 baserunners. Randy Winn (.295/11/75) led the Fish with 103 runs scored, drilled 37 two-base hits and swiped 23 bags. Charles Johnson handled the primary workload behind the dish and swatted 20 long balls.
| LINEUP | POS | WAR | WS |
| Luis Castillo | 2B | 3.12 | 23.37 |
| Edgar Renteria | SS | 4.62 | 25.78 |
| Randy Winn | RF/LF | 2.56 | 19.31 |
| Kevin Millar | 1B | 1.83 | 14.94 |
| Mark Kotsay | CF | 2.15 | 14.21 |
| Miguel Cabrera | 3B/LF | 0.08 | 8.66 |
| Charles Johnson | C | 1.25 | 11.6 |
| Billy McMillon | LF | 0.62 | 5.12 |
| BENCH | POS | total_WAR | total_WS |
| Alex Gonzalez | SS | 1.79 | 20.48 |
| Mike Redmond | C | 0.14 | 1.88 |
| Luis Ugueto | 2B | 0.01 | 0.21 |
| Julio Ramirez | CF | -0.05 | 0 |
| Dave Berg | 2B | -0.41 | 2.37 |
The “Original” 2003 Florida Marlins roster
| Player | POS | WAR | WS | General Manager | Scouting Director |
| Livan Hernandez | SP | 6.33 | 21.08 | Dave Dombrowski | Orrin Freeman |
| Edgar Renteria | SS | 4.62 | 25.78 | Dave Dombrowski | Gary Hughes |
| Luis Castillo | 2B | 3.12 | 23.37 | Dave Dombrowski | Gary Hughes |
| Josh Beckett | SP | 3.04 | 10.93 | Dave Dombrowski | Al Avila |
| Randy Winn | LF | 2.56 | 19.31 | Dave Dombrowski | Gary Hughes |
| Mark Kotsay | CF | 2.15 | 14.21 | Dave Dombrowski | Orrin Freeman |
| Kevin Millar | 1B | 1.83 | 14.94 | Dave Dombrowski | Gary Hughes |
| Alex Gonzalez | SS | 1.79 | 20.48 | Dave Dombrowski | Gary Hughes |
| Felix Heredia | RP | 1.48 | 8.18 | Dave Dombrowski | Gary Hughes |
| Claudio Vargas | SP | 1.41 | 6.65 | Dave Dombrowski | Gary Hughes |
| Charles Johnson | C | 1.25 | 11.6 | Dave Dombrowski | Gary Hughes |
| Billy McMillon | LF | 0.62 | 5.12 | Dave Dombrowski | Gary Hughes |
| Will Cunnane | RP | 0.46 | 3.16 | Dave Dombrowski | Gary Hughes |
| Mike Redmond | C | 0.14 | 1.88 | Dave Dombrowski | Gary Hughes |
| Miguel Cabrera | LF | 0.08 | 8.66 | Dave Dombrowski | Al Avila |
| Nate Robertson | SP | 0.05 | 1.32 | Dave Dombrowski | Al Avila |
| Michael Tejera | SW | 0.01 | 3.19 | Dave Dombrowski | Gary Hughes |
| Luis Ugueto | 2B | 0.01 | 0.21 | Dave Dombrowski | Orrin Freeman |
| Julio Ramirez | CF | -0.05 | 0 | Dave Dombrowski | Gary Hughes |
| Brian Meadows | SP | -0.27 | 3.12 | Dave Dombrowski | Gary Hughes |
| Vic Darensbourg | RP | -0.36 | 0.26 | Dave Dombrowski | Gary Hughes |
| Dave Berg | 2B | -0.41 | 2.37 | Dave Dombrowski | Gary Hughes |
| Jason Pearson | RP | -0.54 | 0 | Dave Dombrowski | Orrin Freeman |
| Hector Almonte | RP | -0.75 | 0 | Dave Dombrowski | Gary Hughes |
| Blaine Neal | RP | -0.95 | 0 | Dave Dombrowski | Orrin Freeman |
| Gary Knotts | SP | -1.05 | 0.73 | Dave Dombrowski | Gary Hughes |
| Kevin Olsen | RP | -1.13 | 0 | Dave Dombrowski | Orrin Freeman |
Honorable Mention
The “Original” 2011 Marlins OWAR: 39.8 OWS: 254 OPW%: .510
Adrian Gonzalez (.338/27/117) and Giancarlo Stanton (.262/34/87) along with batting champion Miguel Cabrera (.344/30/105) form a potent lineup as the Marlins seize the National League Wild Card entry.
On Deck
The “Original” 2013 Diamondbacks
References and Resources
Baseball America – Executive Database
James, Bill, with Jim Henzler. Win Shares. Morton Grove, Ill.: STATS, 2002. Print.
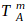 be a random variable for the total batters faced when he allows his mth hit; similarly, let b be P(H) for 2014 Bumgarner and
be a random variable for the total batters faced when he allows his mth hit; similarly, let b be P(H) for 2014 Bumgarner and  be a random variable for the total batters faced when he allows his 1st hit. If 2010 Pitcher A allows his mth hit on the jth batter, he will have a combination of m hits and (j-m) non-hits (outs, walks, sacrifice flies, hit-by-pitches) with the respective probabilities of a and (1-a); meanwhile 2014 Bumgarner will eventually allow his 1st hit on the (j+1)th batter or later and he will have 1 hit and the rest non-hits with the respective probabilities of b and (1-b). We can then sum each jth scenario together for any number of potential batters faced (all j≥m) to create the formula below:
be a random variable for the total batters faced when he allows his 1st hit. If 2010 Pitcher A allows his mth hit on the jth batter, he will have a combination of m hits and (j-m) non-hits (outs, walks, sacrifice flies, hit-by-pitches) with the respective probabilities of a and (1-a); meanwhile 2014 Bumgarner will eventually allow his 1st hit on the (j+1)th batter or later and he will have 1 hit and the rest non-hits with the respective probabilities of b and (1-b). We can then sum each jth scenario together for any number of potential batters faced (all j≥m) to create the formula below:

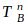 be a random variable for the total batters faced when 2014 Bumgarner allows his nth hit and
be a random variable for the total batters faced when 2014 Bumgarner allows his nth hit and 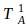 for when 2010 Pitcher A allows his 1st hit. However, instead of directly deducing the probability that 2010 Pitcher A allows 1 hit before 2014 Bumgarner allows his nth hit, we’ll do so indirectly by taking the complement of both the probability that 2014 Bumgarner allows his nth hit before 2010 Pitcher A allows his 1st hit (a variation of our first formula) and the probability that 2014 Bumgarner allows his nth hit and 2010 Pitcher A allows his 1st hit after the same number of batters.
for when 2010 Pitcher A allows his 1st hit. However, instead of directly deducing the probability that 2010 Pitcher A allows 1 hit before 2014 Bumgarner allows his nth hit, we’ll do so indirectly by taking the complement of both the probability that 2014 Bumgarner allows his nth hit before 2010 Pitcher A allows his 1st hit (a variation of our first formula) and the probability that 2014 Bumgarner allows his nth hit and 2010 Pitcher A allows his 1st hit after the same number of batters.