There’s no question that Statcast has revolutionized the way we think about hitting. Now in year three of the Statcast era, everyone from players to stat-heads to the average fan is talking about exit velocities and launch angles. But what can a player do to improve both their exit velocity and launch angle? It all comes down to the mechanics of the swing.

The next great revolution in baseball is leveraging data about swing mechanics to optimize exit velocities and launch angles. It’s a revolution that has already begun. Using technologies developed by companies like Zepp, Blast Motion, and Diamond Kinetics, players and coaches can now get detailed analyses of every swing during practice. Teams are already starting to integrate these swing analyses into their player-development programs. However, none of these sensors are currently being used during MLB games.

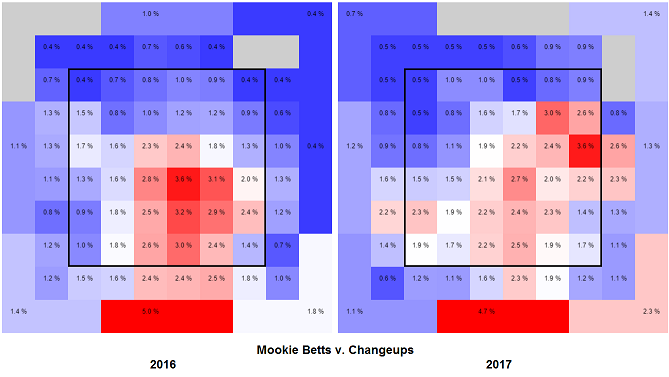
It’s only a matter of time before MLB starts tracking swing data during games, but until then we can use Statcast data and a little physics to reverse engineer the mechanics of the swing. A couple of weeks ago, Eno Sarris and Andrew Perpetua wrote some great articles about the importance of making contact out in front of the plate and how we can infer the contact point from Statcast data. Other than contact point, what are the other important characteristics of a swing? Well, let’s look at Eno’s favorite graphic, from the time Zepp analyzed his swing:

It all comes down to swing speed, attack angle, and timing! The time to impact is probably impossible to get from the Statcast data, so let’s focus on the two remaining metrics: swing speed and attack angle.

Swing speed

Statcast doesn’t measure swing speed directly, but nonetheless reports an estimated swing speed, computed using an algorithm with all the transparency of a black box. In fact, it’s so secretive that estimated swing speeds have all but disappeared from Baseball Savant in recent weeks. Just to find the data, I had to dig up a couple of the saved searches from Alex Chamberlain’s article from a few weeks ago on that topic. Here is the leaderboard of the fastest average estimated swing speeds as reported in that article:

Eno swings like Giancarlo Stanton!

Now, I don’t want to shatter anyone’s dreams of blasting a home run off of a Major League pitcher, but something is clearly off about the data. It turns out that not all reported bat speeds are equal. Physics tells us that as the bat rotates, the barrel (the end) of the bat moves the fastest and that the bat speed decreases in an approximately linear fashion as we move toward the hands. According to Patrick Cherveny, the lead biomechanist for Blast Motion, which is the official swing sensor of the MLB, measuring the barrel speed is essentially meaningless:

“We see some swing speeds where people claim that you get into the 90s. That would make sense if it’s at the end of the bat, but if you hit it at the end of the bat, it’s not going to travel as far because some of the energy is lost in the bat’s vibration. So that kind of a swing speed is essentially ‘false.’ Swing speed is dependent on where you’re measuring on the bat. In order to maximize quality of contact, the best hitters want to hit the ball in the “sweet spot” of the bat.”

Measuring the speed of the bat at the sweet spot, a two-inch-long area whose center is located six inches from the barrel of the bat, Blast Motion reports that MLB players swing the bat between 65 and 85 MPH. Zepp, on the other hand, reports the barrel speed, which accounts for its elevated values. Still, none of the swing-tracking devices on the market report swing speeds as low as those estimated by Statcast.

Let’s see if we can uncover more information about the black-box algorithm used by Statcast to estimate swing speeds. A quick linear regression between average estimated swing speed and average exit velocity for all batters with at least 100 batted ball events (BBE) in a season from 2015-2017 yields an R² of 0.99. Wow! Statcast estimates swing speeds almost entirely from exit-velocity data. No wonder the names at the top of the list are so obvious.

Exit velocity, however, isn’t the only velocity measured by Statcast. We also know the speed of the pitch as it is released from the pitcher’s hand. Thinking about the physics, the bat transfers energy and momentum to the oncoming ball at the point where the bat collides with the ball. Thus, any estimation of swing speed based on Statcast’s EV and pitch speed data represents the speed of the bat at the point where it makes contact with the ball. Since hitters want to hit the ball at the sweet spot, swing speeds estimated from Statcast data should fall in approximately the same range as those measured by Blast Motion.

Much of the research on the physics of bat-ball collisions has been conducted by Dr. Alan Nathan, so let’s start with one of his equations:

EV = e_Av_ball + (1 + e_A)v_bat

where EV is the exit velocity, v_ball is the velocity of the ball before it hits the bat, and v_bat is the velocity of the bat. Here e_A is a fudge factor called the collision efficiency, and depends on the COR of the ball, which was at the center of the juiced-ball controversy, the physical properties of the bat, and the point on the bat in which that bat strikes the ball. Thus, assuming all MLB players use a standard ball and bat, e_A can be viewed as a measure of quality of contact. Nathan found that at the sweet spot of a wood bat, e_A = 0.2. Using that value of e_A and the release speed and exit velocities from Statcast, we can estimate the bat speed for every ball in play. According to Nathan’s pitch-trajectory calculator, the average pitch slows down by 8.4% from the release point to when it crosses the plate, so we’ll also make that adjustment to the release speed reported by Statcast. Here’s the relationship between our physics-based model for swing speed and the estimated swing speed from Statcast/Baseball Savant:

Look at that! When you get a slope of 1 and an intercept of about 0, you know you’ve hit the nail on the head. This must be the equation that Statcast is using to estimate swing speed. After doing a little digging, it appears that Nathan gave them that exact formula, but assumed that the pitch slows down by 10% by the time it crosses the plate.

The problem with this algorithm is it assumes that the hitter always hits the ball at the sweet spot. Nathan’s paper actually shows that e_A varies linearly as a function of EV, from about -0.1 for the weakest hit balls to 0.21 for the best hit, depending on how far from the barrel the bat collides with the ball. To get a good estimate of swing speed, we’ll need to get a better estimate of e_A. Unfortunately, e_A must be computed independently for every hitter due to inherent differences in a hitter’s strength. For instance, when Giancarlo Stanton hits a ball with an EV of 100 MPH, he is making weaker contact than when Billy Hamilton hits a ball 100 MPH.

I calibrated e_A for each hitter with at least 100 BBE in a season by estimating that the average of the top 15 BBE by exit velocity corresponds to e_A =0.21 and the average of the bottom 15 BBE by exit velocity corresponds to e_A = -0.1 for each player. Since e_A and EV are related linearly, we can compute e_A from EV for each player. Finally, I will assume that every player uses a standard 34 in., 32 oz. bat. Since Nathan’s study used a 34 in., 31 oz. bat, I subtracted 0.42 MPH from the estimated swing speeds, because every extra ounce reduces that bat speed by about 0.42 MPH. Here’s a look at our new average estimated swing speeds:

We see that swing speed still correlates strongly with exit velocity, but with a much more reasonable R² value of 0.81. Much of the remaining variance is due to the quality of contact, as estimated by e_A. The colors here show the soft-hit rates from FanGraphs. We can see not only that slower swing speeds result in more soft contact, but also that the regression line strongly divides hitters based on their soft-contact rates. Hitters above the line tend to make better contact and hit the ball more efficiently than those below the line, given their swing speeds.

Knowing the value of e_A also gives us an estimate of where the ball hit the bat in relation to the barrel. Nathan found that e_A ~ d², where d is the distance from the barrel. Since a quadratic function has no inverse, we’re forced to infer d from our computed values of e_A by assuming a linear relationship between the two variables. Once we know where the ball struck the bat, we can also estimate the barrel speed and hand speed, assuming that those speeds are proportional to distance from the axis of rotation.

I have no idea how accurate these estimates are, but they look pretty good! The swing speeds at the point of contact line up nicely with those from Blast Motion (65-85 MPH range and league average of 70 MPH), as do the barrel speeds (Zepp claims 75-95 MPH) and hand speeds (Blast Motion says 23-29 MPH). There’s a lot more uncertainty in the barrel and hand speeds than at the point of contact, because they require additional assumptions about bat size, axis of rotation, and distance from barrel of the point of contact. Even with all of those assumptions, the accuracy probably isn’t much worse than those of the swing-tracking devices on the market today, which claim an uncertainty of about 3-7 MPH for individual swings.

Here are the fastest and slowest average swing speeds in a season during the Statcast era:

At the top of the list we see some well-known sluggers and … Rickie Weeks? Who knew he had such elite bat speed? Unfortunately for him, his average e_A in 2016 was the lowest of any player in the Statcast era, indicating that he was making a ton of weak contact. Weeks is the quintessential over-swinger, whose impressive bat speed is often nullified by a lack of bat control. That’s completely unsurprising for a player’s whose 2016 highlight reel features at least one hack that would make even Charlie Brown blush:

I was also going to include a table of all of the fastest individual swings, until it turned into an exercise in how many times I can write Giancarlo Stanton’s name. He has 18 of the top 19 swings by barrel speed, which tops out at 108 MPH.

Attack Angle

Unlike swing speed, Statcast doesn’t give us an estimate of attack angle. Instead, we’ll again turn to some research done by Dr. Alan Nathan, this time from his 2017 Saberseminar presentation. To better understand the geometry of the bat-ball collision, let’s look at a diagram from his presentation:

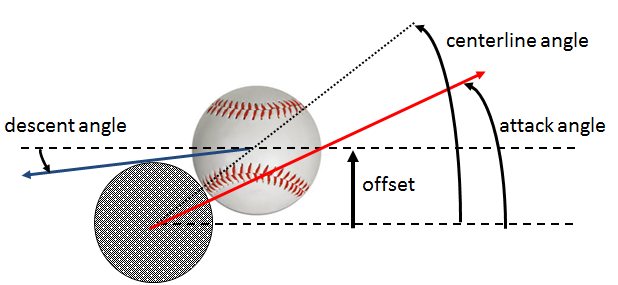
The attack angle, or swing plane, is the angle that the bat is moving at when it hits the ball. Drawing a line between the centers of the bat and ball at the time of impact defines a second angle, called the centerline angle. When a hitter swings the bat such that the attack angle lines up with the centerline angle, he generates his maximum exit velocity and launches the ball at an angle equal to that of the attack angle.

Armed with this information, we can compute the attack angle by looking at the launch angles when a hitter produces his highest exit velocities. Nathan does this by plotting EV against LA for each hitter (below is his figure for Khris Davis’s BBE, whose attack angle is about 20°). He then divides the data, presumably binning the data by launch angle and then pulling out the top few BBE by exit velocity in each bin (red points). Once the data has been divided, a parabola can be fit to the red points, such that the attack angle corresponds to the peak of the parabola.

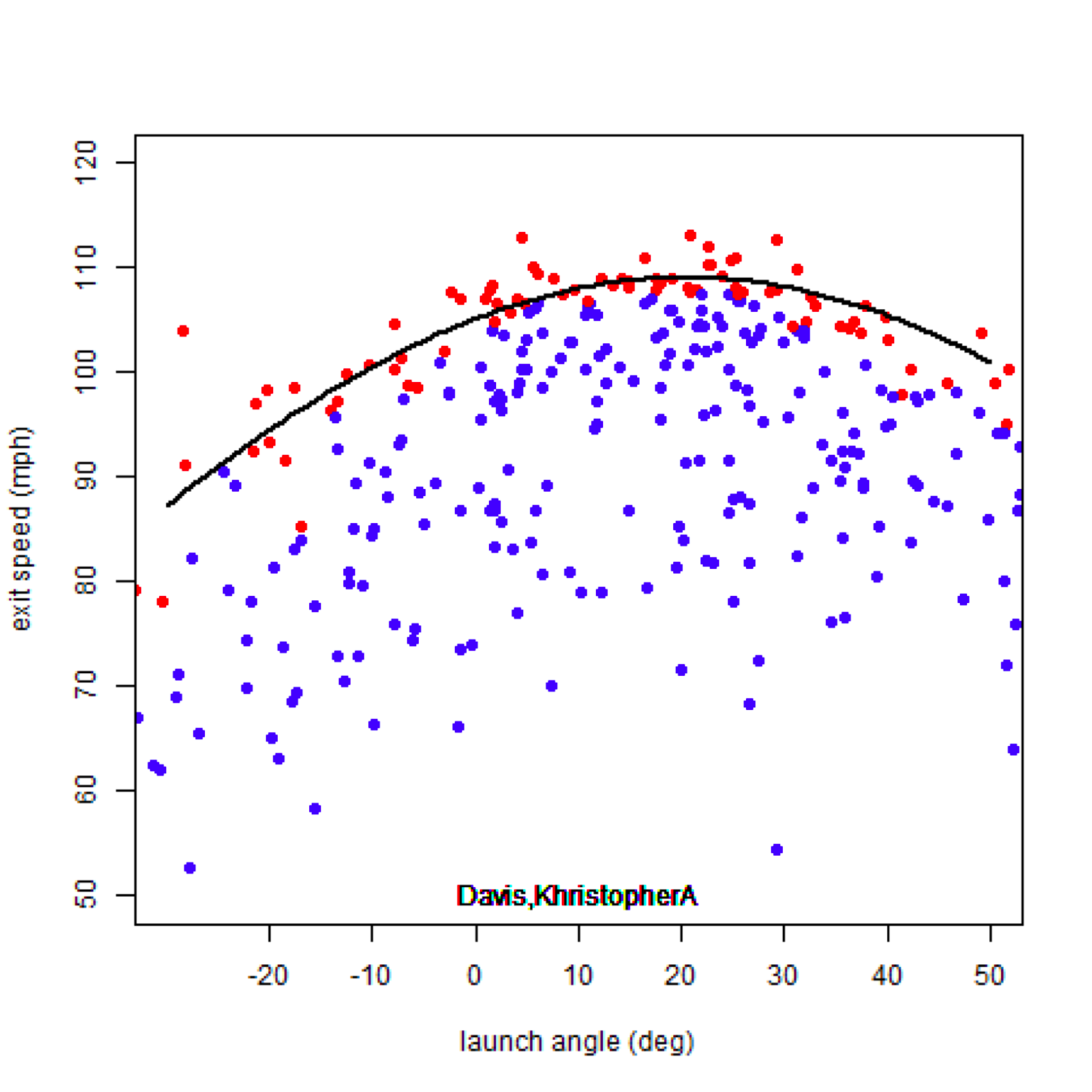
I found that the computed attack angle is fairly sensitive to the number of bins and number of data points in each bin, so this method is far from perfect. Ultimately, I chose the number of bins based on each player’s standard deviation in launch angle (~3° bins), and selected the top 20% of data points by exit velocity. I then computed a second version of attack angle by averaging the launch angles of the top 15 BBE by exit velocity (just as I did when computing swing speeds). Finally, I averaged the values from the two different methods to get a final value for the attack angle.

This method of computing the attack angle gives us what I’ll call the “preferred” attack angle. Batters change their attack angles slightly based on pitch location, but the preferred attack angle represents the plane of a hitter’s natural swing when he gets a good pitch to hit (à la batting practice).

A lot of digital ink has been spilled over the last few years trying to make sense of how to evaluate hitters using launch angles. While a ton of progress has been made, we still have a long way to go. Who knew launch angles could be so complicated? Here, we see a relatively weak correlation between attack angle and launch angle, because launch angle is also strongly dependent a hitter’s aim, timing, and bat speed. While we don’t have any direct measurements of aim or timing, we can see from the color scale that players with flatter swings (lower attack angles) have more margin for error when it comes to timing, and therefore tend to have higher contact rates than players with uppercut swings (larger attack angles).

The fly-ball revolution is even more evident when looking at league-wide attack angles instead of launch angles. There was a lot of buzz before this season about players reworking their swings to increase their launch angle. Not all of them were successful though, as the average launch angle only increased by 0.3°, despite a nearly 2° jump in attack angle.

Here are the highest and lowest preferred attack angles in a season during the Statcast era:

It’s good confirmation to see Ryan Schimpf’s name on this list, though it’s interesting that his attack angle isn’t the extreme outlier that his GB/FB ratio and LA are. An analysis of attack angle may also finally give us an answer to why Brian Doziers’s home runs have gone missing this season. His 2017 batting line is almost identical to that of 2016, except his ISO (and HRs) have plummeted. The biggest difference is his attack angle has skyrocketed from 20° to 29°. We know that the optimal LA for hitting home runs is about 24°, so he’s probably getting too much loft on his fly balls this year. All of these guys at the top of the list would probably benefit by flattening out their swings a bit. Interestingly, Joey Gallo, everyone’s other favorite extreme fly-ball hitter, has an attack angle right at 24° this year. He has built the perfect swing for his batted-ball profile, which explains why he is among the league leaders in HR/FB ratio.

This turned out to be an extremely lengthy primer on swing mechanics, but there plenty of questions that can be tackled with estimates of swing metrics. For instance, can we use swing speed and attack angle to predict future exit velocities and launch angles? How much do hitters reduce their swing speeds on two-strike counts? How do attack angles change with pitch location? But, alas, those questions will have to be answered at a later time.

A complete list of swing speeds and attack angles for players with at least 100 BBE is available here.

If it weren’t for Adam Engel, Carlos Carrasco would have shut out the Chicago White Sox on Wednesday night. It’s hard to believe something stood out to me more than the preceding sentence’s qualifier, but baseball possesses the quality of unpredictability, and I will never complain.

Carrasco is an artist, mixing five pitches with such care that I often find myself gravitating towards his starts despite my lack of association with the Indians’ fan base. On Wednesday, what I noticed more than Engel ruining a shutout was Carrasco veering away from a pitch vital to his repertoire — his changeup. Due to the graces of BrooksBaseball.net, I can confirm the lack of changeup usage was unusual for Carrasco; five instances of the pitch were his second-fewest in any start this season. Wednesday was the longest outing of Carrasco’s season and matched his season-high “game score” of 89 (50 is average) from a battle back on April 22nd against — you guessed it — the White Sox.

Carrasco’s beauty stems from his ability to execute flawlessly with a game plan contrary to what you would expect. His season averages reflect the bigger picture, yet on a given night he can meander in unprecedented directions. My wonder surrounding the lack of his usual third pitch brought me to another contrarian aspect of Carrasco’s game: this changeup possessed the best ground-ball per ball-in-play ratio of any pitch in baseball (min. 200 pitches). 82% of the time when contact is made between the lines, the batted-ball result of this changeup is a ground ball. With 6% of batted balls falling into the “fly-ball” category, Carrasco’s pitch is one of the hardest in baseball to hit in the air.

Does this make it the best changeup in baseball? That depends on what qualities you believe make a changeup great. Per FanGraphs, Clayton Kershaw — shocker — holds the highest pitch value for a changeup at 6.9 runs per 100 pitches (0.0 is an average offering), with Carrasco just behind him. If you subscribe to limiting line drives as the better indicator of changeup success, the honor would go to Stephen Strasburg, who coincidentally gets the most whiffs per swing on his changeup at 51%. I’m not arguing that Carrasco has the best changeup in baseball; I’m highlighting how absurdly hard it is to do anything but hit Carrasco’s changeup on the ground. That in itself deserves as much attention as one that generates excessive swings, or is throw by the left hand of a legend — I tip my hat to you, Mr. Kershaw.

If you read my most recent recent column on the Orioles’ Dylan Bundy — whom I already consider to be “great” (yeah, pretty bold) — you can tell I’ve become intrigued by the Baseball Prospectus rabbit hole that is pitch-tunneling. In as simple terms as you can get, the “tunnel point” is where the hitter has to decide whether or not to swing, with movement more than 2.6 inches between the tunnel point and home plate considered above-average. The concept is fresh, with only bits of hard evidence for suggesting how to correctly apply the statistic, but one of its beliefs makes intuitive sense. In a vacuum, if your pitch moves more than average beyond the tunnel point, it becomes harder to hit. My thinking with Carrasco’s changeup is simple: it must have a lot of downward, “late” break to force hitters into topping the ball at such a high rate.

Ah, if only baseball was that easy.

Carrasco’s pitch sequence of fastball-changeup is his fourth-most commonly used pitch pair; it doesn’t stand out in terms of post-tunnel break among his other pitch pairings, nor when you compare that break back to the league average for a typical fastball-changeup sequence. What it does stand out on is something called “flight-time differential.” Carrasco’s .0223 is the third-lowest in baseball among pitchers who have thrown a fastball-changeup sequence more than 50 times. This stat is another way to show velocity differences between pitches. The short flight-time differential holds up when we observe Carrasco’s 5.7 mph difference between his average fastball and changeup velocities (fourth-smallest, qualified pitchers).

Good news: this all jives with Harry Pavlidis’ research. Harder changeups with smaller velocity differentials between that pitcher’s fastball means more ground balls, while a larger velocity gap between the two pitches means more whiffs. While ground-ball inducers tend to throw their change earlier in counts, whiff inducers favor the pitch as a put-away offering. While that sentence isn’t all-encompassing, Carrasco’s deviation from conformity continues.

As with most right-handed pitchers, Carrasco tends to throw his changeup to left-handed bats substantially more than right-handed bats, favoring the benefits of arm-side movement a changeup generally possesses due to the pronation of a pitcher’s hand. But unlike conventional thought that suggests the pitch’s ground-ball rate is such that early-count looks are likely, Carrasco throws the pitch more as he gets deeper into counts.

Just as Carrasco plays second fiddle to Corey Kluber in the Indians rotation, his changeup plays second fiddle to his slider, both allowing for rampant underappreciation. The pitch is so good this year that Carrasco has muddied the stigma that high-velocity, or low-velocity differential, changeups should remain early-count offerings. Once again, Carrasco is veering from the path of predictability.

Even after four seasons where progressive improvement hasn’t ceased, due to injuries we still haven’t seen a 200-inning campaign from the righty. 2018 will be his age-31 season, and as father time comes knocking, it’s unfortunate that we may be observing the tail end of Carrasco’s peak performance. With the Indians firmly intertwined with the phrase “playoff bound,” Carrasco will get his first reps on an October mound. If history provides any indication of the future, we know Carrasco will both stand out from him predecessors and succeed.

In regards to an obscure September outing and the lack of changeup usage, digging deeper might unearth logical reasoning, but with Carrasco, I think mystery adds to the legend of an under-the-radar arm.

I can be found on Twitter – @LanceBrozdow – tweeting about the greatest of all games.

A version of this post can be found on my website, BigThreeSports.

When calling balls and strikes, consistency matters. As long as an umpire always calls borderline pitches the same way within a game, players seem to accept variations from the rule book strike zone. While there have been many excellent analyses of umpire accuracy, these studies tend to focus on conformity to a fixed zone, rather than on the dependability of those calls.

Disgruntled fans can turn to Brooks Baseball’s strike zone plots when they feel an umpire has had a bad game against their team. For example, the following zone map seems egregiously bad:

The calls seem very capricious, especially on the outside (right) of the zone. Balls (in green) are found in the same locations as strikes (in red), and some called strikes landed much further outside than pitches that were called balls.

On the other hand, the zone map below appears fairly consistent:

One might quibble with a couple of the outside calls, but the called strikes, for the most part, are contained within a ring of balls. Notice also that pitches in the lower-inside corner were consistently called balls. While this umpire didn’t establish a perfectly rectangular zone, he did establish a consistent zone; neither pitcher got those calls on the inside corner, and hitters on both teams generally knew what to expect.

In this post, I will propose a metric for assessing the inconsistency of an umpire’s strike zone. This metric does not assess how well the umpire conformed to the rule-book zone or the consensus MLB zone. Rather, it uses some tools from computational geometry to compare the overall shape formed by called strikes with the shape formed by the called balls.

Data from MLB Advanced Media describes each pitch as an ordered pair (p_x, p_z), representing the left/right and up/down positions of the ball as it crosses the front of the plate. This pitch-tracking data includes measurements of each batter’s stance, which can be used to normalize the up/down positions to account for batters of different heights. If we draw a scatterplot of these adjusted positions corresponding to called strikes during a given game, the outline of the points represents what we define as the umpire’s established strike zone.

More precisely, the established strike zone is what mathematicians call the “convex hull” of these points. If you draw the points on a sheet of paper, the convex hull is what would remain if you trimmed the paper as much as possible, without removing any points, using only straight cuts that go all the way across the sheet.

A similar construction describes the alpha hull of a set of points: replace the paper cutter with a hole punch that can only punch out circular holes of a given radius. Punch out as much of the paper as possible, without removing any of the points, and what remains is the alpha hull. Unlike the convex hull, the alpha hull can have empty region in its interior. We can therefore define an umpire’s established ball zone as the alpha hull of points corresponding to called balls.

A consistently-called game should have the property that the established ball zone lies entirely outside of the established strike zone. Any called strikes that fall within the established ball zone (and any balls inside the established strike zone) are inconsistent calls. Since it is reasonable to expect that a consistent umpire will establish different zones depending on the handedness of the batter, we calculate established zones separately for left- and right-handed batters, and then count the number of inconsistent calls from each side of the plate.

Over the course of a game, an umpire’s inconsistency index is the ratio of inconsistent calls to the total number of calls made. For example, the plots below show the established strike and ball zones for the game between the Reds and the Giants on May 12, 2017. Of the 239 calls made that day by the home-plate umpire, 14 balls fell within the established strike zone, while 5 called strikes landed in the established ball zone, resulting in an inconsistency index of (14+5)/239 ≈ 0.0795.

How do MLB umpires fare under this metric? Quite well, actually. Using data for the 2017 season (through September 10), the average inconsistency index for all games called was 0.0396. Moreover, of the 2112 games analyzed, there were 183 games where the home-plate umpire scored an inconsistency index of 0.0, meaning that the established strike zone fell completely within the established ball zone. The 15 most consistent umpires, based on their average inconsistency index over all games called in 2017, are given in the table below.

While the strike zones of these umpires may not robotically correspond to the rectangles we see on MLB broadcasts, the zones they do establish are remarkably consistent.

Graphs and computations in this article were produced in R, using the PitchRx and alphahull packages. Source code for producing these examples is available on GitHub.

*Apologies for the bad writing, as this is my first-ever community post on FanGraphs.*

At the time of this writing, it’s been seven days since rosters expanded in the major leagues. Still, the International League (AAA) home-run leader has yet to appear in a major-league game season. Since the 2000 season, there have been three International League home-run champions that had not appeared in a major-league game that same season. Bryce Brentz, leading that league with 31 home runs and winner of the Triple-A Home Run Derby, is about to be fourth.

The Red Sox of the old days had the reputation of being offensive powerhouses by working long at-bats and possessing big power in the middle of the lineup. This year, it’s been quite the opposite. Red Sox pitching has been absolutely amazing this season; the pitching WAR is tied for second place (with the Dodgers) while also having the fourth-best ERA in the majors at 3.76 ERA. Compared to how great the Red Sox pitching is, the hitting is bad. REALLY BAD. Their pitching and hitting are night and day. It’s well documented that the Red Sox aren’t hitting for power this year, sitting dead last in the AL with only 146 home runs. Perhaps teams don’t need to hit home runs to be productive? The advanced metrics say otherwise. Out of all qualified players, the Red Sox batter with the highest wRC+ is Dustin Pedroia who has a 106 wRC+, and 2016 MVP runner-up Mookie Betts is running a 101 wRC+. All in all, the Red Sox offense has been below average this season. The emergence of Rafael Devers and the spark that Eduardo Nunez has provided to the Red Sox have both softened the blow, but there still appears to be a glaring weakness.

In the absence of David Ortiz, Hanley Ramirez was supposed to step up and become a middle-of-the-order power threat. What’s inexcusable is his performance versus lefties this year. As someone who’s destroyed lefties his entire career, he’s suddenly slashing .194/.312/.419 against lefties in 2017. His career OPS/wRC+ vs. lefties is .902 OPS and 138 wRC+ respectively.

HanRam has been having one of his worst seasons hitting-wise versus lefties. Despite insisting that he will improve against lefties, Red Sox fans have yet to see the results come out.

Another factor is Chris Young’s performance. Chris Young was brought to Boston to club lefties. He’s always been able to hit them, and his splits against lefties prove just that.

Discarding 2014 and this current season, that chart is a thing of beauty. Chris Young’s performance this year has been concerning; he hasn’t had an RBI since August 6! Chris Young was a player who was specifically brought onto this roster for the specific purpose of facing tough lefties. He is having his worst season hitting lefties yet. As of right now, he is batting only .184 against lefties this season with one home run, four extra-base hits, and four RBI.

The Red Sox need Bryce Brentz. Brentz certainly has the prospect pedigree, being drafted by Red Sox in the first round of the 2010 Major League Baseball Draft out of South-Doyle High School. Once rated as the No. 5 prospect in the Red Sox system, he stood out with his plus raw power. FanGraphs’ Kiley McDaniel had this to say about him a few years back:

“Brentz has easy plus raw power from the right side and is a solid athlete, but it doesn’t translate to defense, where his fringy arm limits him to left field. There’s some holes, lots of swing and miss and trouble with spin from right-handed pitchers, but also 20-25 homer power with a floor of a solid platoon bat.”

The key word here is “solid platoon bat,” something he’s finally evolved into this year. This year, down in Triple-A, when facing left-handed hitters, Brentz was hitting .279 with nine home runs, 25 RBI, and 17 walks. His OPS against lefties is 391 points higher than Chris Young’s OPS in the majors this season (.957 OPS). Rhys Hoskins, who took the majors by storm, was the only player ahead of him in the IL in terms of wRC+.

Brentz had worked with PawSox hitting coach Rich Gedman this past offseason, which has suddenly changed him into someone who destroys left-handed pitchers and is at least passable against righties. By introducing a toe-tapping procedure to Bryce Brentz, Gedman has turned him into a major home-run threat. I think it’s time to believe that after 6+ seasons in the minor leagues, Bryce Brentz finally has things figured out.

The basis behind why Dave Dombrowski won’t call up Bryce Brentz is, to say the least, questionable.

Dave Dombrowski said IL HR champ Bryce Brentz willl not get callup from Pawtucket. Brentz hit 31 HR but no 40-man roster spot available.

— Nick Cafardo (@nickcafardo) September 4, 2017

No 40-man roster spot available? C’mon. Off the top of my head, I could name off a few minor leaguers who don’t deserve this spot over Brentz. Most notably, the walk machine himself, Henry Owens. Owens was sent down to Double-A to work on mechanics, but instead, he’s walking 8.68 batters per 9. Ben Taylor, who made the Opening Day roster for the Red Sox, has had considerable minor-league success, but the results haven’t translated to the majors. He’ll most likely end up as a career middle reliever or minor-league journeyman. Sure, these players have their uses, but they don’t deserve their spots as much as Brentz does. After his hard work in the offseason, his performance needs to warrant him a 40-man spot. Additionally, after Chris Young becomes a free agent next year, Brentz can serve as the fourth outfield for the Red Sox in 2018. If the Red Sox don’t add Brentz to the 40-man by the offseason, he’ll become a free agent. It’s almost guaranteed that a team such as the Athletics or the Reds would be willing to give him a chance.

There’s another problem. At the moment, the Red Sox really lack good pinch-hitters. When your best hitters off the bench are Brock Holt, Sandy Leon, Rajai Davis, etc, the outcome looks really bleak. Brentz is a minor-league veteran who is a power threat off the bench, something the Sox currently lack. His career hasn’t progressed much (until now at least) since he shot himself in the leg during the spring training of 2013. If fact, if you go to some online forums, his spring-training incident has created tons of puns that have to with guns; the former top prospect had become a joke. Similar to the rest of the “comeback” stories (such as Rich Hill, Eric Thames, etc) that fans have loved to watch in recent seasons, the story of Bryce Brentz should warm the hearts of fans.

Something else stands out. During the Red Sox’s recent 19-inning game, this tweet was sent out. While it may have been mostly a joke, it really exemplifies the lack of power the Red Sox have.

Brentz would have already homered this inning

— Red Sox Stats (@redsoxstats) September 6, 2017

This really speaks about the Red Sox offense. Bryce Brentz is the spark plug that they need.

As seen by the Nationals calling up Victor Robles just the other day (considered late), the Red Sox certainly still have time to call up Bryce Brentz. If any Red Sox personnel is reading this, the rest of Red Sox Nation and I have this to say to you: “Hey, It’s worth giving Brentz a shot.” He’s deserved it.

When the Houston Astros sent two of their top pitching prospects, Vince Velasquez and Mark Appel, to the Philadelphia Phillies for Ken Giles in December 2015, they were expecting an excellent flame-throwing reliever, and possibly their closer of the future. In his first two years in the league, Giles amassed a 1.56 ERA in 115.2 innings. His work as a setup man/closer went largely unappreciated due to the losing nature of the Phillies, but Giles pitched like one of the best relievers in the game.

But his first year in Houston did not go as planned. Giles couldn’t maintain a hold of the closer job, as he blew five of his 20 save opportunities and finished with a 4.11 ERA. His 2.86 FIP proved he might have suffered from bad luck, and he still displayed incredible stuff (nearly 14 K/9), but he did not execute as expected or needed for the Astros.

2017 has been a different story for Giles. His 29 saves rank ninth in the league, and he has blown only three opportunities this season. His 2.30 ERA is legitimate, supported by a 2.14 FIP. Giles has been one of the best closers in baseball, but his name is hardly mentioned among the top guys in the league. And he’s been especially locked in of late.

Last night (September 5th at the time of writing this), Giles struck out the side in a 10-pitch inning to earn the save against the Seattle Mariners. The only ball he threw came when the batter barely checked his swing. Here he is hitting triple digits on the outside corner to get Ben Gamel looking and close out the game:

It was the second night in a row that he struck out the side for 1-2-3 ninth.

Since June 7th, Giles has a minuscule 0.86 ERA and .147 average against. FIP will rarely support a mark that low, but his 1.57 mark in that category is still exceptional. He’s striking out more batters and walking fewer, accumulating a K-BB% of 31.3%.

Giles has given up one run since July 16th, in 20.1 innings of work. His FIP is under 1, at an absurd 0.82, and he’s sporting a ridiculous 45.1% K-BB% in that time. He has also show the ability to be stretched out of late, as he has gone 1.2 or more innings in three of his last ten appearances. What has made him so effective this season?

It all starts with the slider for Giles, which ranks third in run value among relievers at 12.9 runs. Run values aren’t the best metric, but they definitely give you an idea of the effectiveness of a pitch. Just look at it:

The pitch starts at the “TEXAS” on Rougned Odor’s jersey and finishes below his knees. There is about nothing a hitter can do with that.

Look at a heat map, by pitcher viewpoint, of Giles slider’s location. He is burying the majority of his sliders along the bottom of the zone. Now look at a heat map of the average against the pitch, by zone. Where the majority of the pitches are going, hitters aren’t doing much with. At all. Per Brooks Baseball, hitters have only put the ball in fair territory on 25% of their swings at the pitch. They rarely put the ball in play, and they don’t do much with it when they do.

But this is actually not new for Giles. He was third last year in slider run value among relievers, at 12.6 runs. Where Giles has greatly improved his effectiveness is with his fastball. It was worth a run value of -13.3 in 2016, but it’s currently sitting at 3.4 this year. It has not been incredible, but paired with the slider, it doesn’t need to be.

Here is a comparison of his fastball in 2016 vs. 2017:

The batted-ball numbers are down across the board. He’s throwing it in the strike zone more often as well, which would cause you to expect he is pitching more to contact with the pitch. However, the Contact% has steeply declined, and the swinging-strike rate is way up. Obviously, with a 137 wRC+ allowed this year, the pitch is still not great. But when you have a slider running a -14 wRC+, it does not need to be.

Here is a heat map comparison of the two pitches: 2016 vs. 2017

The spray is much tighter in 2017, and he is throwing across the middle of the zone a whole lot less. Improved command of a pitch will obviously lead to more success. But another element might be involved in the improvement of his fastball. Giles has added nearly four inches of horizontal movement this year, from -1.7 to -5.6.

A 2016 fastball:

And the fastball from last night again:

The run to the right on the pitch is clear. Movement of any kind will always help to keep a hitter off balance, and while we can’t be sure, it looks like this may be what has given life to Giles’ fastball. His confidence with the pitch has grown, as his usage of it exploded from roughly 50% to 68.4% in August. And it appears this improved fastball may be keying his emergence as one the best closers in the game.

Giles lost some respect and notoriety with his poor 2016. But with the year he has put together so far, especially the way he’s pitching of late, he has earned all of that, and then some, back. He’s locking down the back of Houston’s bullpen. The Cleveland Indians displayed the importance of relievers in the playoffs last season, so don’t be too surprised if Giles is at the forefront of a charge to the World Series for the best team in the American League.

Confusion and “what ifs” among the industry on Orioles’ starter Dylan Bundy are everywhere, so I’ll cut through the present state of takes like a knife: Bundy is a great starting pitcher.

Red flags and disapproval rise because of circumstances surrounding Bundy that make it easy to dislike his past, present, and even future. I get it. His struggles with injuries, and Baltimore notoriously failing to develop viable starters, are two tenets the anti-Bundy fan club champions. But when any pitcher puts together multiple oh-my-god outings at different points in a season, underlying causes for those sprinkles of success reveal important trends.

One theme in Bundy’s flashes of success is a pitch the Orioles nixed as an option in the past, fearing excessive stress on his elbow. Some call it a slider, others a cutter, and the Baltimore Sun moderates the argument with a simple hyphen. It’s a pitch that possesses average to below-average break on both horizontal and vertical planes, yet still generates impressive swing-and-miss capabilities. Bundy’s cutter-slider — the Baltimore Sun method of indifference — sits fifth in whiffs generated per swing among pitches that Baseball Prospectus classifies as a “slider” (95th percentile, >200 pitches thrown). The four names above Bundy are Corey Kluber, Carlos Carrasco, Max Scherzer, and Mike Clevinger. Three objectively great pitchers, and an up-and-comer who I’ve profiled before.

Despite possessing average movement, the pitch might benefit from Bundy’s ability to tunnel all of his pitches.

Baseball Prospectus has taken the plunge in quantifying “tunneling” to the masses, and although intimidating at first, the theory makes intuitive sense. The “tunnel point” is the point in time where hitters have to make a decision whether or not to swing, and if hacking, where to do so. Above-average movement past the tunnel point would seemingly make a pitch harder to hit.

Bundy’s “Break Differential” — how much spin-induced movement is generated between the tunnel point and home plate — is 3.7 inches, substantially higher than the major-league average mark of 2.6 inches (87th percentile, 1,000+ pitch pairs). Bundy is also in the 85th percentile for a metric that signals how closely nestled his pitches are at the point of tunnel, known as the “Break:Tunnel Ratio.” We can’t say with certainty that his cutter-slider is the main culprit for this particular kind of niche success, but with the knowledge he uses it more often than any other non-four-seam pitch — especially in two-strike counts — we can infer it has some inflationary quality in this new-age stat.

Inflator number two might be the pitch that takes a back seat to Bundy’s cutter-slider, his changeup.

Bundy’s approach against right-handers is 75% fastball and cutter-slider usage, while versus left-handers, his mix in terms of offspeed is relatively even between the cutter-slider and his other three pitches, with this changeup basking in the spotlight of favoritism at 20%. Bundy uses this changeup when he needs a strike, as the pitch is seen more than three times more often when he is behind in the count rather than ahead, regardless of batter handedness.

After he gets back into counts with his changeup, he turns to the cutter-slider to put away hitters.

The frequency at which he uses his slider, at any point in an at bat, is what simple analysis says correlates to his overall success.

If just throwing his slider more was the reason for his recent success, Bundy’s xFIP in particular wouldn’t be half a run lower in his most recent set of games.

Jeff Sullivan of FanGraphs mentions that Bundy has gone up in the zone to lefties more often in August, but the effect that approach has on his other pitchers stands out the most. Combing through Bundy’s approach to left-handers and right-handers, you’ll notice an uptick in slider usage, but perhaps the most impressive change is his new ability to strike out left-handers. While his strikeout rate versus right-handers has stayed around the 24-28% mark for most of the season — reaching a high of near 30% in his most recent starts — lefties’ ability to solve the righty have dwindled.

Meddling around 12% for the first four months of the season, in Bundy’s most recent seven starts, that left-hander strikeout rate has more than doubled to 26%. This was the missing piece that allowed him to post a 28% strikeout rate over than span. His ability to pitch up in the zone to lefties allowed for the other pitches in his arsenal to flourish, and as a result, Bundy has become more confident with his cutter-slider, evidenced by its usage. The key is not only using the cutter-slider more, but combining that usage with an approach that makes the pitch more effective, particularly to left-handed bats. Overall trends in Bundy’s game have allowed individual pitches to become more effective, and with his innate ability to deceive hitters post-tunnel point, Baltimore is seeing the potential start to blossom.

In Dylan Bundy, the Orioles have something their fan base has longed for; a 24-year-old arm with an enviable arsenal and the ability to tunnel his pitches in a way that makes each independent part more deadly. There have been growing pains, but his tools have become skills at the major-league level, and it’s hard for me to doubt his intermittent dominance isn’t a sign of greater polishing. Although it would be naive to say his cutter usage is directly tied to good starts, Bundy’s Labor Day meltdown is highlighted by reliance on his fastball and his lowest cutter-slider usage since the beginning of July — sub 20%. Whether the downtick in cutter-slider usage on Monday was because because of comfort with the pitch, or a want to focus elsewhere, at least the Orioles know where Bundy’s strengths are when he spins a great outing.

Use your offspeed, Bundy, and may the baseball gods grant you health like no other. Those are the primary factors to make the step from possessing great skills to being an elite arm.

A version of this post can be found at BigThreeSports.com

Lance Brozdowski can be found on Twitter as well, @LanceBrozdow

The regression that I am going to run analyzes whether sabermetric statistics, more specifically WAR, have a greater impact on MVP voting than traditional statistics. This is important to the sport because MVP voting helps players garner a good reputation. It also affects how the front office of each major-league baseball team goes about acquiring specific players. In fact, the salaries of players can be affected by MVP voting, especially if that player is in the last year of his contract and is preparing to become a free agent. In turn, acquiring high-level or MVP-type players can potentially improve overall team performance, which would result in an increase in attendance, and therefore, the team would have an increase in revenue.

The data set that I have chosen to look at is the 2014 results for MVP voting for both the American and National Leagues. Also, I will look at the individual statistics for each of the players that received votes. From this relationship, the independent variables would be the player statistics (batting average, home runs, RBI, WAR) and the dependent variable would the number of votes that each player receives. This is because certain statistics are bound to affect whether one player receives more votes than another. Essentially, what I am trying to prove is that one set of statistics is a better indicator of player ability and player contribution than the other set. Bill James was one of the first to expound upon sabermetrics when he wrote a series of books known as Baseball Abstract in the 1980s. Many other baseball historians, such as Pete Palmer and John Thorn, have written books detailing and introducing the concept of sabermetric statistics. While many books have been written and studies have been done about sabermetrics, no one has really done a study about the accuracy and influence that sabermetrics can have on statisticians, writers, fans, and teams.

For this regression, I analyzed only position players (non-pitchers) to prevent confusion due to the use of different statistics which are required to analyze pitchers separately. After the running of the regression, it appears that the WAR has a greater impact on MVP voting than home runs, RBI, batting average, and stolen bases. However, the two statistics that seem to have the greatest impact on MVP voting are On-Base Percentage (OBP) and Slugging Percentage (SLG). WAR has a positive slope of 35.9 while SLG has a positive slope of 2,535.7. The coefficient of correlation (R) is 0.87 and this seems to indicate that the nature of the relationship in this regression is positive. Also, the fact that the coefficient of correlation is closer to 1 indicates that there is a significant relationship between respective statistics and their influence on MVP voting. The coefficient of determination (R^2) is 0.76. This shows that just about 76% of the MVP voting results can be attributed to the certain statistics of a specific player. For instance, in the American League, Mike Trout led the league in WAR and RBI, and was third in SLG. Since those two statistics were the most impactful, they definitely contributed to Mike Trout being named the MVP. Therefore, this relationship is positive, and some statistics have a significantly higher impact on MVP voting than others. Once again, based on the regression, SLG seems to be the most impactful statistic, and stolen bases were the least impactful.

After analyzing the results of the regression, I ran a hypothesis test to determine the population coefficient of correlation. The level of significance for this hypothesis test was 0.05. The null hypothesis was that p=0; in other words, there is no significant relationship between any statistic and MVP voting. The alternative hypothesis is that p>0, p<0 and that there is a significant relationship between certain statistics and MVP voting. The degrees of freedom for this hypothesis test was 21. The t-critical value turned out to be about 2.1. I tested each individual test statistic and discovered that there is a significant relationship between MVP voting and RBI, SLG, and WAR since the t-calc for those variables was greater than 2.1.

To further test this theory, I also did an ANOVA. I wanted to test the variation of MVP voting when compared to certain statistics at the 0.05 level of significance. The degrees of freedom1 was 7 and the degree of freedom 2 was 21. Therefore the f-critical value turned out to be 2.5. F-Calc from the ANOVA was 9.6. Since F-calc is greater than the critical value, we prove that, once again, there is a significant relationship between certain statistics and MVP voting.

Next, I did a test for the least squares regression. For the least squares regression you have to do a test for three separate things. They are normality, homoscedasticity, and independence. To test for normality, I looked at the normal probability plot. The points on this plot seemed to be curved slightly, therefore, the residuals are not normally distributed. To test for homoscedasticity, we look at the residual plots for each of the x variables. Since most of these variables neither increase nor decrease as x increases or decreases, these variables are homoscedastic. To test for independence, you would have to run another regression. This time, it would be a simple regression using the same x variables; however, each residual is the x variable for the next one. To test for independence, you would also have to do a hypothesis test. The null hypothesis would be that bi=0 and the alternative hypothesis would be that bi>0, bi<0. If bi is equal to 0 than the residuals are independent. The level of significance is 0.05 and the degrees of freedom would be 30. The t-critical value came out to be about 1.7. T-calc turned out to be greater, which means that the residual values are not independent.

In conclusion, the initial multiple regression that I ran showed a significant relationship between certain statistics and MVP voting. Despite the fact that the residuals were not independent, the other tests that I ran showed over and over again that the same statistics that the regression stated were impactful on MVP voting were still impactful after I ran other tests. Thus, it seems that the sabermetric statistic WAR did have more of an impact on MVP voting than most of the traditional statistics such as batting average and home runs. While sabermetric statistics are a new trend in baseball analytics, they will not replace the traditional statistics such as batting average, home runs, and runs batted in, simply because those statistics have been used since the early days of baseball. Fans and statisticians alike will continue to use both traditional and sabermetric statistics to analyze player performance.

There are many other statistics that I could’ve analyzed for this regression. In fact, pitching statistics are completely different from the statistics that I used in this regression for position players. However, the statistics that I did use proved to be effective in proving that, in fact, some statistics do have a considerably greater impact on MVP voting than some statistics that some people simply assume are not relevant or needed in order to analyze player performance and contributions. Also, for this regression, I only analyzed the offensive statistics for the position players. Defensive statistics such as defensive runs saved (DRS) and defensive WAR are also important statistics that many baseball statisticians look into when evaluating player performance. Overall, the possibilities for this regression are endless, and even though there may never be a definitive statistic that everyone agrees upon for analyzing player performance, all of the statistics that I used in this regression, as well as many others, will continue to remain relevant in the game of baseball for many years to come.

2014 American League MVP Voting Results

2014 National League MVP voting results

American League MVP Candidate statistics: (league ranks for respective statistics in parenthesis)

National League MVP candidate statistics: (league ranks for respective statistics in parenthesis)

http://www.seanlahman.com/baseball-archive/sabermetrics/sabermetric-manifesto/

www.baseball-reference.com       http://sabr.org/sabermetrics/statistics

http://bbwaa.com/14-al-mvp/                                            

http://bbwaa.com/14-nl-mvp/

As I’m sure you all know, Statcast allows us to measure the launch angle and velocity for each batted ball. These measurements afford us the ability to estimate precisely the expected wOBA value of every batted ball. Due to the skills of the opposing defense (as well as, admittedly, factors like luck, weather, and ballpark quirks), these estimated wOBA values are often drastically different from their actual values. That is the idea behind Expected Runs Saved (xRS), a metric that I have created to measure team defense. What follows is a discussion of the xRS methodology and some results.

The methodology: The calculation of xRS is actually quite simple. I started by downloading Statcast data from Opening Day through August 29th using Python’s pybaseball module. I then created a dataset consisting of all fair batted balls (excluding home runs) during that time frame. Conveniently, the downloaded data already has the expected wOBA value (based on exit velocity and launch angle), and the actual wOBA value (based on the outcome of the play) for each batted ball. Since we want to penalize teams for making errors, I changed the actual wOBA values for errors from 0 to 0.9 (the value of a single). Then all we have to do is take the average of each metric by team, find the difference, convert that to run values, and we have Expected Runs Saved.

Note that xRS is quite a bit more simplistic than UZR or DRS, as it doesn’t include any of the defensive value derived from keeping baserunners from taking the extra base, preventing steals, turning double plays, etc. While these surely play a role in run prevention, they are less important than converting batted balls into outs, and since I have a full-time job I decided to keep it simple and ignore them.

The results: Let’s start with the most obvious question: which team has the best defense?

It’s the Angels, and it’s not particularly close. While their pitchers have allowed a lot of hard contact (.323 batted-ball xwOBA, 28th in baseball), their actual wOBA on contact is 2nd in baseball at .291, trailing only the Dodgers (.284), who, as Jeff Sullivan recently noted, excel at inducing weak contact.

On the opposite end of the spectrum are the Blue Jays, who have been generally good at generating weak contact (.305 batted-ball xwOBA, 5th in baseball) but terrible at converting those weakly hit balls into outs (.322 batted ball wOBA, 28th in baseball).

In both cases UZR tends to agree, ranking the Angels and Blue Jays 1st and 27th, respectively. Due to (I think) the simplicity of the model, the run values for xRS are quite a bit more extreme than those of either UZR or DRS, but it ranks the teams in generally the same order. At the very least, xRS doesn’t disagree with UZR and DRS much more than the latter two disagree with each other.

Two teams that xRS likes a lot more than UZR and DRS are the Mariners (2nd in xRS, 11th in UZR, 15th in DRS) and Yankees (4th in xRS, 13th in both UZR and DRS). Meanwhile, it dislikes the Dodgers (12th in xRS, 3rd in UZR, 1st in DRS) relative to the other metrics, as well as the Reds (28th in xRS, 5th in UZR, 4th in DRS). Why is this happening? I really don’t know. Could be some defensive components I have left out of xRS, could be ballpark effects, or it could just be that defensive metrics are weird. It remains a mystery. Such is baseball, and such is life.

Mookie Betts was incredible in 2016. As the third-best player in the Majors, he posted a 7.9 fWAR. But this year has been different. His .261/.341/.434 triple slash line is a far cry from the one he posted last season of .318/.363/.534. His 101 wRC+ tells us he’s producing runs at a rate that is barely above league average, while also revealing a lot of his value has come from his defense.

And yet, he’s still on pace for about 4.5 fWAR, which still makes him one of the game’s top assets. He continues to be awesome, but a different kind, and different enough to ask “what’s changed?”

There are some significant differences from last year to this year in Betts’ contact profile. In general, he’s swinging less. Like, a lot less. Last year he took the 20th-most pitches in the league. This year, he’s taking the fourth-most. He’s also swinging at fewer pitches in the zone, while making more contact when he goes outside it. That’s an odd combination for a player so disciplined at the plate. It suggests pitchers have adjusted to Betts and that he might have picked up on it, but that he hasn’t quite countered yet.

And though it helps us see what’s fueling a lower triple slash this year and, by matter of course, lower WAR, it doesn’t tell us how pitchers have adjusted to Betts. He’s seeing just about the same pitch mix this season as last, save for one thing. He’s getting about 22% sliders this year, or an additional 5% more than in 2016.

His wOBA against sliders is just .276 this season. That’s lower than what even his expected wOBA against sliders was last year, which he topped by 57 points. And like dominoes, this one push is impacting other pitches he’s seeing.

Changeups are also giving Betts considerable problems, and it could be because he’s been oddly less patient with them than other offerings in 2017. Despite seeing almost the same exact amount this year as last, and swinging at them at a nearly identical rate, his weighted pitch value against the offering is more dramatic than any other. He’s managing an unimpressive -0.43 mark this season. In 2016? It was at 3.67. He’s gone from waiting for changeups to show up in his wheelhouse to swinging at them freely. It’s extremely uncharacteristic for Betts, and it’s yielded just a .260 wOBA against the pitch.

Consider how the changeup is designed to induce weak contact, how it can often fade and drop away toward the lower outside corner of the zone, and how sliders drive to the same portion of the plate. Pitchers seem to have found a way to sequence their stuff against Betts to thoroughly influence the damage he can create with the bat.

This is particularly true with right-handers, against whom Betts is batting only .253 in 2017. Last year, he hit .331 against them. And because the league features about two and a half as many right-handers as southpaws, the trouble for Betts becomes emphasized that much more.

Mookie Betts is still exceptional. He’s still demonstrating elite control of the zone, as evidenced by a walk rate that equals his K rate. But there appear to be plate adjustments that will be necessary for him to make if he’s to return to being one of the game’s absolute best.

This is probably not going to be a long article but I was curious which players fit the Hoskins profile best in recent history. Carson already established the Hoskins profile as a guy who hits the ball in the air and makes contact.

For that, I searched first basemen that played from 2002 to 2017. I used 2002 because that is the year we started to have batted-ball data. It also means that it mostly covers a high-K era, although it got more extreme recently. As a cut-off, I used 1500 PAs played. 96 players fulfill those criteria.

First, I filtered for an ISO of .200 or greater. I also filtered for a BB% of greater than 9% (because Hoskins also walks), a K% of 20% or smaller, and finally a ground-ball rate of 40% or under.

That leaves a list of just eight names:

The list is a pretty good group. It averages 23 career WAR, a 127 wRC+ and a .273/.367/.503 line. The only downside there might be is that the fly-ball profile could supress BABIP some. The group has a .287 BABIP which is below the league average of .300 during that time span, especially if you consider how hard those guys hit the ball. That means that those guys do underperform their K/BB/ISO profile a little bit. For example, Konerko has a very good power/contact/discipline profile that by my math points to more of a 140+ wRC+, but his actual wRC+ is 120. That is the disadvantage of that extreme profile — you are losing some BABIP to fly outs, especially if you hit more balls in the high fly ball range, which tend to be either HRs or outs, and even more so if there is a slightly elevated pop-up rate coming in conjunction with the fly balls.

But overall that doesn’t matter that much if the K/BB/ISO profile is that good; those guys are all really good hitters even with a slightly lower BABIP. Just expect Hoskins’ hit tool to play under his contact rate a little bit due to that Bautista-like profile (who also had that lower-BABIP, pulled-fly-ball profile with great contact and walk rate).

That means Hoskins might be a .265 hitter despite above-average contact, which also makes his SLG play a little bit down on his power, but he should still get on base on a very good clip and produce excellent power. Just be a little careful when looking at his power, contact, and discipline if you want to bank him for a .300 average/.600 SLG for your fantasy team. He might pay some cost with his elevating that doesn’t come in the form of Ks, but BABIP. But nonetheless he should be very good, even if it is “just” a Konerko/Teixeira type of player and not the next Miggy like some Philly fans probably think right now.