Now that I have gone through the individual cohorts in parts 1, 2, 3, and 4 (click them if you need some background in what I am doing).  To start I will show you three charts with some simple, and I don’t think overly shocking, things to remember.  Then I will get into some regressions that will hopefully help explain what I think is going on.  Keep in mind throughout this that the groups that should be trusted most are the larger cohorts, 22 to 26 year old first full seasons, as the others might have some sample size issues and you will see in these charts that 19 and 20 year cohorts don’t behave well in almost all cases.

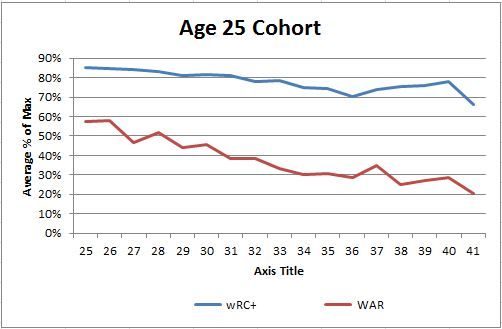
First up is this:

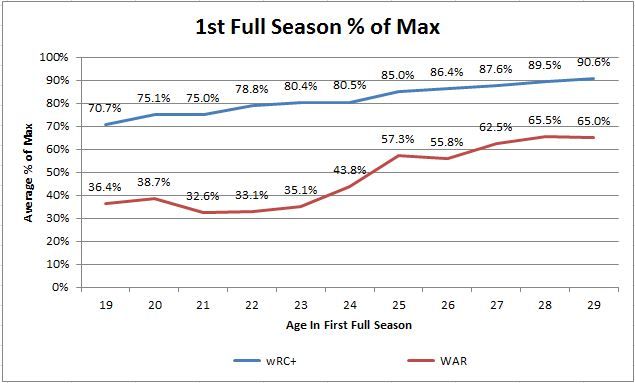
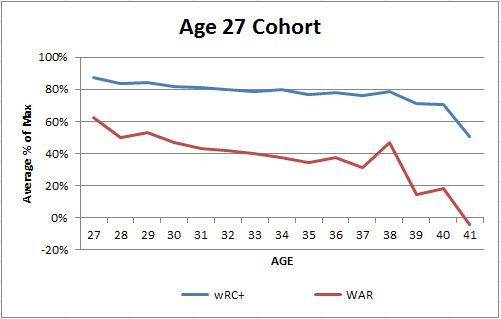
If you look at the average percent of max for each cohort in their first season, it shows an upward sloping line for both hitting skill and overall value.  The younger cohorts are therefore farther from their peak production when they show up in the league and should be expected to grow if they stick around.  You see a lot higher percentages for wRC+ versus WAR mostly from a scaling and volatility difference.  Going from 1 WAR to 2 WAR is a 100% improvement and not terribly hard to do.  Going from 80 wRC+ to 160 wRC+ is much, much harder, and 1 standard deviation for wRC+ is about 25% of the average while it is almost 100% of average for WAR so wRC+ is significantly less volatile relatively.

Those characteristics mean that randomness around your true talent level means that 50% of max WAR on average means that the cohort might already be at peak true talent level from 24/25 years old and due to volatility it is hard to get very close to 100%, but the hitting gets much closer.  Anyway, players coming up later are much closer to their peak on average and just don’t have much room to grow.  Next let’s look at the two stats, starting with wRC+, at overall level rather than percent of max production:

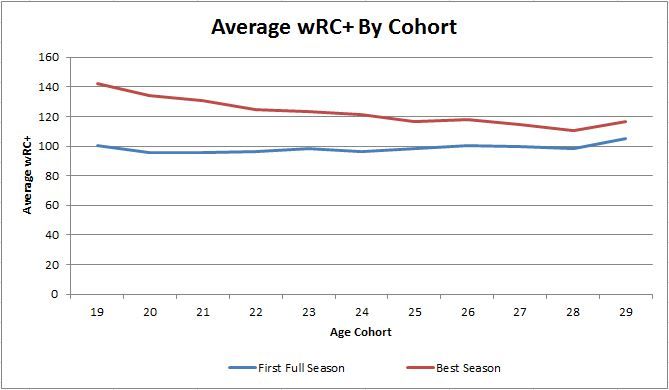
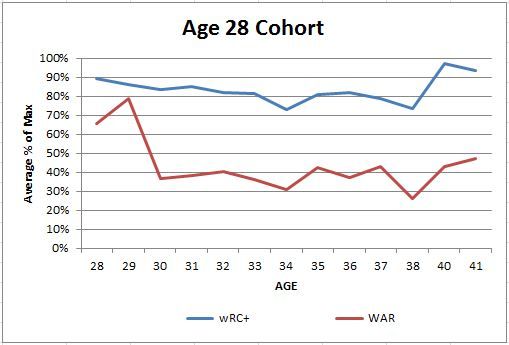
In the first full season each cohort performs at a very similar level, and the older cohorts might actually slightly outperform the younger.  That is a pretty flat line for first year average.  If you take each players best season though, the younger cohorts destroy the older cohorts.  Every cohort before age 25 has an average best of 120 wRC+ or better, so most of the players in those cohorts are going to put up at least one season in the Chase Utley of the last 2 years range, which is pretty good.  After that the difference between the average of the first full season and the peak shrinks down to 10 to 20 wRC+, well within one standard deviation, so the peak looks more like a season where luck pushed a player above average rather than a change in expected performance level.  That’s why we saw players in the cohorts after 24 seem to be at peak and only decline after entering the league.  WAR behaves similarly:

Again, 19 and 20 year olds are few and far between, but seriously and average best season of 5 to 6 WAR is pretty staggering as last year only 12 position players made it to 6 WAR or better.  On average the cohorts mostly show up around 1.5 WAR in their first season, and again the older cohorts probably are a little better in their first year.  The best season averages are again much better with a downward slope on the best season averages that starts to flatten out in the mid to late 20s, and I think it is easier to see on this chart than the first.  On average players enter the league at about the same level hitting and as overall producers, but those who can manage that at a younger age (before 25) generally go on to higher performance levels than the players who debut older.

Next I am going to show three regression outputs to try and explain what I think is important to remember for aging of players.  I will try to explain what I am doing so that if you don’t have a background in regression analysis you can still get the point.  If you do have a regression background, know that I am focusing on a couple of key ingredients so they are not intended to be perfect models.  Mostly I am trying to use data to illustrate a point.

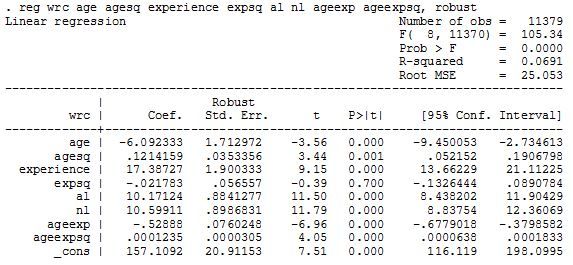
So first I went back to all data and ran this OLS specification with wRC+ as the dependent variable.  I was looking at two things, we expect age to affect players in a nonlinear fashion (aging CURVE) so I put in an age and age squared term and did the same for experience where 1st year in the big leagues is 1, 2nd is 2, etc.  AL and NL are probably not necessary but are controlled for in wRC+ and I just went ahead and stripped that part out since I had it there in dummy variable form.  Then I added interaction terms where I multiplied age and experience to see if the combination of the two is important rather than them acting independently.  The only term that came back insignificant was experience square which gave experience a purely linear relationship to hitting performance and also shows why this would be a bad model to lean on in predicting player performance.

The coefficient for experience is 17.4 so the model is saying each year of experience helps the player’s wRC+ increase by an average of that amount.  Other factors, age and age/experience interaction are negative and working against that, but this strong positive experience coefficient makes it so that if you model out a generic player of any cohort they get better at hitting for an unreasonable amount of time before the negative coefficients catch up because age*experience as a multiplier is getting bigger faster.  For the age 21 cohort the first year a player would start to decline would therefor be predicted in year 13 at age 33, and for the 27 cohort year 10 age 36 going against everything we know.

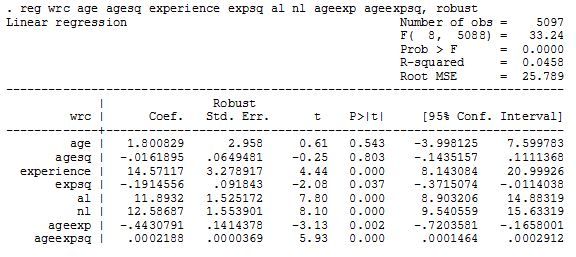
This is I think mostly due to survivor bias (I have discussed this before).  Let me show you what causes this with another regression output.  In this one I intentionally bias the sample by only including players who have 10 or more full seasons.  This reduces my original number of player from 2,054 down to 390, so about 19% of position players that get a full season end up with 10 or more for their career according to this set of players and they have an inordinate effect on a regression of the whole group.

In the first regression there were 11,379 observations (player years), but 5,097 came from this group of players that made it 10+ years.  That means 19% of the players are making up almost 45% of data being used!  They are also in general the best players, which is why they stuck around for so long and thus made it look like experience was a huge positive above.  Within just these players you see that effect is still strong with an experience coefficient of 14.6, but it is no longer linear as experience squared is now a significant negative showing the curve I would expect of experience.  Experience, at least in my expectation, should be beneficial to a player, but have diminishing returns (less effect in each year of experience) and this model shows that.  If you play this model out for the same cohorts I did before it does a better job of showing the peak in the mid 20s, but then continuing production for a lot longer than we would expect for an average player.  That’s fine, I just wanted to show why it is hard to tell how the general player ages because of the undue power of the players who stick around for so long.

Finally, I want to show you one more regression and discuss some things I think are important for aging in baseball players.  In this one I focused on differencing of wRC+ (e.g. year 2 minus year 1) and created a variable called sustained.  Sustained is a dummy variable that shows years in which a player was better than a previous wRC+ level in two consecutive years.  So if a player had a wRC+ of 100, then 112 the next year and 108 the next it was sustaining higher performance.  Also, since I am using differences in wRC+ instead of the values themselves all 1st year player data is gone since there is nothing to difference it from.  This could be considered as biasing data again, but since we are looking at aging curves players need to stick in the league to see anything so I am doing a study only on those players rather than one and dones.  Here is the output, then more discussion:

Sustained is now the dependent variable, and it is a binomial variable, so I had to move to a logit model.  That means the coefficients are now hard to directly interpret them since they are log odds of the sustained outcome rather than actual units of wRC+ as before.  This model does show what I believe to be the case after breaking all of the aging curve into age cohorts.  It does not show age or age squared as significant, it is showing that experience matters and that the interaction of experience and age matters.  Players who can get major league experience benefit most from getting that experience younger.  There is an obvious endogeneity issue here that that it may be the other way around, players that can get to the majors younger are better players.  I think there is truth in both statements though.

Yes, a player who can handle playing at the major league level at a younger age is likely better and should have a higher expected peak.  On top of that though, the model here is showing that the experience for such a player may also matter.  Playing against better competition makes players better, this is a commonly held belief and there is research to back it up if you want to go over to Google Scholar if you want to search around and read some formal pieces on that topic.  For an anecdotal example let’s look at a couple of players. Jose Guillen came up at 21 and muddled around for several years posting 82, 83, 67, and 88 wRC+ numbers in from 1997 through 2000, only got 145 and 259 plate appearances the next two years, and then finally put up a 138 wRC+ followed by three more above average seasons.  Around the same time there was a guy named Travis Lee who was not in the majors until 23 and posted a 102 wRC+ as a rookie.  He hung around for awhile with a peak of 112 wRC+ in 2003, but had a pretty unspectacular career.

Would Travis Lee have been able to put up an 82 wRC+ a couple years before his 102 at age 23?  I have no idea, but it is possible that if he had, and had two more years experience before that 1998 season that was his rookie year that he might have developed very differently.  The interaction term of age and experience is therefore very important in my opinion.  The model shows that experience is an arc that first increases, peaks, and then decreases in probability of reach new sustained performance levels.  If you look at it in conjunction with the age times experience and squared term of age and experience it shows that the probability of reaching a new and higher level of production is higher for a younger cohort (I’ll forgo posting the numbers for expediency), peaks in the mid 20s, and then drops off fairly quickly.  That is what the aging curve probably looks like based on all I have done so far.

We know, in 2014, that lineup construction has little effect on winning. And yet, it’s not any less frustrating when managers set their batting orders in ways that seem to defy any semblance of logic. Lineup construction matters to us. We may know it’s not terribly important, but we’re fascinated in spite of ourselves.

The lineup position subject to the most debate is probably leadoff. Multiple writers and analysts have noted that players who would make the best leadoff hitters are normally too valuable to use in the leadoff position. Bill James wrote in his New Historical Abstract, “All of the greatest leadoff men … would be guys who aren’t leadoff men, starting with Ted Williams … if you had two Ted Williamses, and could afford to use one of them as a leadoff man, he would be the greatest leadoff man who ever lived.”

Every method I’ve seen to determine great leadoff batters produces names like Ted Williams, Barry Bonds, Mickey Mantle, Ty Cobb … players who are probably better suited to the second through fourth spots in the batting order. I think I’ve found a simple method that solves the problem. I’ve always been interested in singles hitters who walk. It’s a skill set that matches our image of the prototypical leadoff batter.

Most fans agree that a good leadoff man should get on base and run the bases well. Most fans further agree that a player who both gets on base and hits with power is more valuable a little later in the order, where he can drive in runs. If we accept that we probably can’t have two Ted Williamses, a realistic ideal of the leadoff batter has a high on-base percentage but doesn’t hit with a lot of power.

With this in mind, I’m adapting a stat I’ve talked about elsewhere to identify optimal leadoff men: OBP minus ISO. In my head, I’ve always called this reverse ISO, but that’s sort of a misnomer, and it’s a little unwieldy, so from here on let’s call this stat combination Leadoff Rating, or LOR. We know a good leadoff man gets on base, but most players with high on-base percentage are great all-around hitters. We know power hitters are usually better suited to other spots in the batting order, but many players with low ISO just aren’t that great. By subtracting isolated power from OBP, we can identify players specially suited to hitting leadoff.

This stat does not include baserunning (because I have no idea how to incorporate it with two percentages) but it turns out not to matter very much. A significant majority of players who rank well in LOR were also accomplished baserunners, and base stealers in particular. Among the top 300 hitters of all time (basically everyone with 2,000 career hits), I found a fairly strong positive correlation between LOR and SB (r=.465). The relationship is weaker if you only look at 1947-present (r=.356), but a degree of positive correlation is clear. In both data sets, n=300.

When you calculate LOR for the all-time top 300 hitters, the leader is Billy Hamilton. That’s Sliding Billy Hamilton, the Hall of Fame outfielder for Philadelphia and Boston in the 1890s, not the rookie phenom for the Cincinnati Reds. The original Hamilton retired with 1,782 singles, 1,187 bases on balls, and 376 extra-base hits. He hit .344/.455/.432, with an ISO of just .088, and an OBP higher than his slugging percentage. Hamilton also stole 912 bases. He is a superb example of the hitter we’re looking for, and he leads the new stat by a huge margin. His .367 LOR rates 12% higher than second-place Eddie Collins (.328). Here’s the top 75: Read the rest of this entry »

This will cover the last set of cohorts, click the links for parts 1, 2, and 3 if you want more info on what I am doing or read on if you are already up to speed.

Age 27 Cohort:

This group started at 173 players with 54 only playing one season leaving 119 for my purposes, and they averaged 5 full seasons each.  Out of the 119, 49 (41%) maxed out their wRC+ in their first full season and 44 (37%) maxed WAR.  Both of the groups that maxed out in year one averaged 3.2 full seasons in the big leagues.

The same thing we have seen since the age 25 cohort continues, a clearly declining performance trend in aggregate from the time they show up until they leave.  In year 1, these players are hitting on average at nearly 90% of their max, so there is almost no chance of a large increase in subsequent seasons.

Age 28 Cohort:

Sample sizes are going to start becoming a big issue again as only 110 started and 38 only played one 300+ PA season.  The remaining 72 averaged only 3.7 full seasons.  For those that were maxing wRC+ or WAR in year one, both groups included 32 of the 72 (44%) and averaged 2.7 seasons and 3 full seasons respectively.

The chart does show an increase in WAR from year 1 to 2 do to an anomaly, but the hitting shows the 90% of peak on average and decreasing from there.  You can ignore the spikes in age 40 and 41 seasons as there was only one player accounted for there, Davey Lopes, who happened to hit pretty well those two seasons.  Without him it drops off like all of the others and ends at age 38.  You can see that by WAR the entirety of their decline is pretty much done by 30 years old, only their third seasons and thus the short careers.

Age 29 Cohort:

This group is nearing the point where it might be worth ignoring anything you see with a starting group of 62 that gets whittled down to 41 players with more than one full season.  Those 41 averaged 4.6 full seasons in their careers, longer than the 28-year-olds because of a few guys that hung around awhile and the small sample.  One was Hideki Matsui who was a professional long before 29, but not in the United States.  I will discuss two others in a moment.  Out of our 41 players here 23 (56%) had their max wRC+ in their first full season, and almost 50%, 20 out of the 41 had their best WAR.  At a coin flip for whether we have seen their best or not immediately we have definitely hit the point where any real growth as a player is unlikely or purely luck driven.  Those two groups of year one max wRC+ and WAR had average career lengths of 3.7 and 3.1 years respectively.

Like the last group we see a little uptick at the end, and these were two of the odd players from this group that hung around.  Actually, Raul Ibanez is still hanging around currently in Minnesota with the Royals, and the other is a former Royal too in Matt Stairs.  Again, in reality this group is pretty much all declining from year 1 on and almost all are finished by their late 30s.  There is a large spike in WAR for ages 32 and 33 and a smaller corresponding one in wRC+ because 4 players had their best season at 32 and 5 players at 33 which is a significant amount out of a pool of 41 players.  Those two years along with the first full season of the cohort comprise over 70% of the players and so it is probably just a sample size issue that we see the early 30s uptick here.

I am done with the cohorts, or at least running through them all the first time.  Players that play their first full season at 30 or older were mostly ignored.  There were 92 of them total and about 80% of them maxed in year one or only had one full season, so to chart a growth pattern would be ludicrous for the other 18 to 20 players who didn’t all come up at the same age.  Next I will summarize this all and try and point out several other things that I learned from breaking these cohorts apart so that you can get the full picture, or at least as much of the picture as I have managed to see.

The Charleston RiverDogs, the Yankees’ low-A affiliate, has rostered several of the team’s more interesting prospects this year, with Luis Severino, Ian Clarkin, Aaron Judge, Abiatal Avelino, Miguel Andujar, Luis Torrens, Gosuke Katoh, and Tyler Wade all having spent time in Charleston thus far. A few of these players are still teenagers, and despite having promising potential, are very raw in terms of their overall development. Despite being just 19-years-old, infielders Avelino, Andujar, Katoh, and Wade spent the entire first half in Charleston with varrying degrees of success. Avelino (108 wRC+) hit fairly well before going down with injury, but Andujar (78 wRC+), Katoh (79 wRC+), and Wade (98 wRC+) have looked a bit over-matched at the plate so far.

These players have been facing pitchers two or three years older than them, so it’s hard be too critical of their poor batting lines; and the fact that they’re even playing in full season ball as teenagers is an accomplishment on its own. Still, performance obviously matters, and you’d prefer to see them hit well than not. But it’s hard to know how much weight should be put on their stat lines. Should we be worried that Gosuke Katoh’s striking out 35% of the time? Or should we still be more focused on the tools that got him drafted in the second round last year? It’s a little hard to say.

To get a better idea of what to make of these guys’ performances, I turned to the reams of minor league data compiled over the last couple of decades. Below, you’ll find some heat maps representing the likelihood that a player will play in the majors based on his low-A stats as a teenager. “Average Power” refers to players with an ISO within .025 of their league’s average, and within each panel, walk rate above league average and strikeout rate above league average occupy the X and Y axes respectively. I considered all 321 player seasons where a teenager logged at least 400 PA’s from 1995-2008.

A couple things to keep in mind before I delve into the results:

1) This methodology measures the likelihood that a player made it to the majors and doesn’t take into account how well he played upon arriving. So a player with one big league game is counted the same as a player who went on to have a Hall of Fame-caliber career. A stat that predicts a player’s making the majors may also predict his level of big league success, but that’s not something I attempt to quantify here.

2) This methodology does not account for a player’s defensive skill or position. Obviously, a weak-hitting catcher or shortstop is more likely to crack the majors than a weak-hitting first baseman, but defensive skill is a little hard to quantify for minor leaguers. Prospects change positions all the time and there’s a good chance any given A-baller won’t stick at his current position as he navigates through three more minor league levels.

Overall, there’s not a ton of predictability here: There are examples of players who made it — or didn’t make it — from nearly every corner of every heat map. Players like Rocco Baldelli, Austin Jackson, Jhonny Peralta, and Pablo Sandoval, turned into fine hitters despite scuffling as teenagers, yet plenty of others hit for good power and put up healthy plate discipline numbers, only to flop at the higher levels. Jeff Goldbach, Nick Weglarz, and Mike Whitlock all raked in A-ball, but never made it to the show. Stats alone can’t tell us everything, but there are definitely some obvious trends. Most notably, players who hit for power appear to be much more likely to play in the majors than those who don’t. Completely ignoring strikeouts and walks, 70% players from the high power group made it to the bigs compared to 65% of players with average power and just 44% from the low power demographic. Plate discipline stats seem to matter a little, but power is clearly king.

The heat maps give a nice visual of what’s happening, but don’t really give us a precise estimate of how likely these players are to make it. To better quantify each player’s chances, I ran a probit regression analysis on this group of players. In a nutshell, a probit tells us how a variety of inputs can predict the probability of an event that has two possible outcomes. In this case, it shows that hitter’s strikeout rate, isolated power, and BABIP are predictive of whether or not he’ll play in the majors.

It’s worth pointing out that there are some obvious flaws in this model. As previously mentioned, it doesn’t consider defense, so if an elite defensive shortstop and a lumbering first baseman had the same batting line, they would receive the same probability, which obviously doesn’t seem right. It also doesn’t take scouting reports into account. We all know that there’s more to a player’s potential than his stat line, especially for minor leaguers; and in some cases, a good scouting report is worth more than a dog’s age of statistical regressions. Still, I think it does a good job of slapping an unbiased probability on a player’s MLB chances. For those interested, here’s the R output from my model:

Without getting too technical, the “Estimate” column basically tells us (in Z-scores) how a change in each stat affects a player’s MLB likelihood. As you’d expect, players with higher strikeout rates are less likely to crack the majors, while players with higher power and higher BABIPs have a better shot. Interestingly, walk rate was not statistically significant in predicting whether or not he’ll reach the big leagues. This might be partly due to the relatively small sample of players, but it’s probably safe to say that a player’s walk rate isn’t a make-or-break. Several players — including Erick Aybar, Michael Barrett, Engel Beltre, and A.J. Pierzynski — managed to reach baseball’s highest level despite walking around 3% of the time in their first tastes of full-season ball, while Mike Whitlock and Nick Weglarz fizzled after walking over 15% of the time.

That’s well and good, but what does it tell us about today’s prospects? Here’s what we get by applying my model to all low-A teenagers with at least 200 PA’s (I also included Abi Avelino, who’s logged 131). What stands out to me is how few players are true long-shots. Of the 36 players, two thirds are more likely than not to make it to the bigs and only one player gets less than a 27% chance. If a player’s talented enough to play in full season ball at 19, there’s a good chance he’ll make it to the majors one way or another.

There are some highly-touted prospects on this list, but other than J.P. Crawford, they aren’t among the names listed near the top. Reese McGuire, Dominic Smith, and Clint Frazier all graced top 100 lists in the pre-season, but have had disappointing power outputs this year, which has lead to such mediocre probabilities. Instead, most of the top ranked players are relatively fringy prospects who have broken out in a big way this year.

As for the Yankees’ prospects, the model thinks Avelino has a pretty good shot at making it, but is relatively low on the others. Even so, Andujar and Wade both have around a 50-50 chance, which isn’t too bad — especially when you consider the model ignores their defensive skills. Things don’t look as promising for Katoh, who’s struck out a ton and hit for only modest power. The lone bright spot in Katoh’s line is his 12% walk rate, which unfortunately for him, proved un-predictive of a player’s big league future.

Lists of baseball’s most underrated players are often interesting and thought-provoking exercises, because by definition they focus on players that tend to get less attention than they should. However, there isn’t an easy way to definitively say how players are “rated” by baseball followers. Writers often just list off players who have the attributes that they are looking for (grit, plate discipline, small market players, etc.), which isn’t a bad way of doing it.

However, there is a more scientific way of approaching a list like this. We could look at how many people are doing Google searches for specific players. It wouldn’t exactly tell us what players are most underrated, but it can tell us which players should be getting more attention; these two things are very tightly correlated. The key difference is that plenty of players get attention for things that don’t necessarily mean they are considered good players. Ryan Braun got a lot of attention during his steroid drama, Robinson Cano was heavily talked about during free agency, and people search for Carlos Santana because of this and this. But when good players draw very little interest from fans, they’re probably underrated. But the term I’ll use is under-popular.

Using Google’s Adwords Keyword Tool, I gathered the data on every player who has achieved a WAR of at least 3.0 since the beginning of the 2013 season. A regression model with those 132 players showed that an additional 1 WAR was worth 6,000 Google searches per month – not too shabby.

Here is a plot of these players, with the expected amount of Google searches on the horizontal axis, and the actual amount of searches on the vertical. While the keyword tool was incredibly useful, it rounds numbers when they get too high, and you can see a handful of players were rounded off to exactly 165,000 searches per month (FYI, these players were Mike Trout, Miguel Cabrera, David Ortiz, Robinson Cano, Bryce Harper, and Yasiel Puig). Derek Jeter has roughly double that amount, but his WAR did not qualify him for this list.

There are a lot of players who have played very well the last two years who are by no means household names. Welington Castillo has put up 3.8 WAR since the start of 2013, A.J. Pollock has been worth 6.1 wins, and Brian Dozier 5.8. In order to really measure who the most under-popular players are, I’ll use two methods. The first is just to simply subtract how many Google searches were expected and how many there really were.

According to this measurement, Josh Donaldson is the most under-popular player in baseball, because he should have been looked up 53,000 times per month more often than he was (68k vs. 15k). That’s a big difference. There are some excellent players on this list, with many players who have an argument as the best or one of the few best players at their position. But for the most part, these are well known players who should just be more well known.

A different way to measure under-popularity, and the way I think is more telling, is to find the ratio between expected and actual searches, as opposed to just subtracting. For instance, is Edwin Encarnacion more under-popular than, say, Luis Valbuena? Encarnacion should have gotten 41,000 searches per month, but actually only got 18,000. Valbuena, however, played like someone who should have been searched 20,000 times, but was only Googled 2,400 per month. Since I believe Valbuena’s numbers are more out of whack, I prefer the second method.

Here are the top 20 players using that measurement, where we see how many times a player was searched as a percentage of how many times you would expect them to be:

Jarrod Dyson has quietly become a well above average baseball player. In about 800 career PA, Dyson has a WAR of 6.8. That is All-Star level production. His elite fielding and baserunning skills (which have combined to be worth more than 3 wins these last two years) make his wRC+ of 91 more than acceptable.

A.J. Pollock appears high on both lists, and for great reason. This year he is quietly hitting .316/.366/.554, after putting up 3.6 WAR last year.

This method of establishing players who deserve more credit for their play certainly has some flaws. WAR is not the only way to measure how good a player is, and Google searches are not a perfect representation of how popular or famous players are. However, it takes away the guess work and opinions from the standard underrated player lists, and in that there is some value.

In case you missed parts 1 and 2, you can follow the links especially back to one if you want to see what I am doing.  Otherwise it is time to look at the 24 year old cohort:

There were 362 players in this group, 64 of which only had one season of 300+ PAs, leaving us with 298 in the sample.  Those 298 averaged 7.2 years of full seasons.  Almost 21% of them (62 total) had their best season in year one according to wRC+, and for war it was just below 20% (59).  For those players the average career length was 4.3 and 4 years respectively.  I’m going to start speeding up the discussion only highlighting things of interest so that we can get to a more comprehensive picture.

The 24 cohort chart shows a couple of years of modest improvement before starting their decline though wRC+ stays pretty flat until age 30 or so.  We have seen some similar patters up to this point, but those are going to end with the next group.

Age 25 Cohort:

This group was comprised of 343 players in total.  After taking out the 59 that only had one season I had 284 left at an average number of 5.9 full seasons.  About 30% of those players had their best season in their first full big league chance (86 for wRC+ and 87 for WAR) with average length of career for the 1st year max group of 4 years for wRC+ and 3.7 for WAR.

This is where this cohort is getting more interesting.  They seem to only decline as a group after their first full season.  There doesn’t seem to be any appreciable increase in hitting or overall performance throughout their careers.  You will also see that they are therefore nearer their max as a group out of the gate as well.  Once I am through all of the cohorts we can discuss overall threshold of performance relative to these which will help us understand everything that is going on hopefully.

Age 26 Cohort:

Here is where the sample sizes start to shrink again as we get to ages where a lot of players have either quit or will never make it.  There are still 238 players in this group so it is relatively large (4th largest cohort), and 64 had only one full season leaving a group of 174 players who on average had 5.2 full seasons.  65 (37%) maxed out their wRC+ in year 1 along with 54 (31%) maxing WAR right off the bat.  Those groups averaged 3.6 full seasons and 3.3 respectively.

Like the last group, this group seems to max out on average in their first year and are declining by their late 20s.  They keep up 80 or near 80% of their max in hitting into their mid 30s, but that I think is going to prove out as being two things.  The first will be survivorship issues since on average most of this group retired or were forced out of the game around age 31, and the second being that their starting threshold won’t be as high and will be easier to stay near.

We are getting close.  I will try and blow through the late 20s before the end of the week so I can summarize and give some things that I think are of interest overall.

I. Introduction

In the statistics driven sport of baseball, the fans who once enjoyed recording each game in their scorecard have become less accepting of what they observe and now seek to validate each observation with statistics.  If the current statistics cannot support these observations, then they will seek new and authenticated statistics.

The following sections contain formulas for statistics I have not encountered, yet piqued my curiosity, regarding the 2010 Giants’ World Series starting rotation.  Built around Tim Lincecum, Matt Cain, Jonathan Sanchez, and Madison Bumgarner, the 2010 Giants’ strength was indeed starting pitching.  Each player was picked from the Giants farm system, three of them would throw a no-hitter (or perfecto) as a Giant, and of course they were the 2010 World Series champions.  Throw in a pair of Cy Young awards (Lincecum), another championship two years later (Cain, Bumgarner, Lincecum), eight all-star appearances between them (Cain, Bumgarner, Lincecum), and this rotation is highly decorated.  But were they an elite rotation?

II. Perfectos & No-No’s

It certainly seems rare to have a trio of no-hit pitchers on the same team, let alone home-grown and on the same championship team.  No-hitters and perfect games factor in the tangible (a pitcher’s ability to get a batter out and the range of the defense behind him) and the intangible (the fortitude to not buckle with each accumulated out).  Tim Lincecum, Matt Cain, and Jonathan Sanchez each accomplished this feat before reaching 217th career starts, but how many starts would we have expected from each pitcher to throw a no-hitter or perfect game?  What is the probability of a no-hitter or perfect game for each pitcher?  We definitely need to savor these rare feats.  Based on the history of starting pitchers with career multiple no-hitters, it is unlikely that any of them will throw a no-hitter or perfect game again.  Nevermind, it happened again for Lincecum a few days ago.

First we deduce the probability of a perfect game from the probability of 27 consecutive outs:

Table 2.1: Perfect Game Probabilities by Pitcher

The probability of a perfect game is calculated for each pitcher (above) using their exact career on-base percentage (OBP rounded to three digits) through the 2013 season.  Based on these calculations, we would expect 1 in 12,152 of Matt Cains starts to be perfect.  Although it didn’t take 12,152 starts to reach this plateau, he achieved his perfecto by his 216th start.  For Tim Lincecum, we would expect 1 in 19,622 starts to be perfect; but starting even 800 starts in a career is very farfetched.   Durable pitchers like Roger Clemens and Greg Maddux only started as many as 707 and 740 games respectively in their careers and neither threw a perfect game nor a no-hitter.  No matter how elite or if Hall of Fame bound, throwing a perfect game for any starting pitcher is very unlikely and never guaranteed.  However, that infinitesimal chance does exist.  The probability that Jonathan Sanchez would throw a perfect game is a barely existent chance of 1 in 94,488, but he was one error away from a throwing a perfect game during his no-hitter.

The structure of a no-hitter is very similar to a perfect game with the requirement of 27 outs, but we include the possibility of bb walks and hbp hit-by-pitches (where bb+hbp≥1) randomly interspersed between these outs (with the 27th out the last occurrence of the game).  We exclude the chance of an error because it is not directly attributed to any ability of the pitcher.  In total, a starting pitcher will face 27+bb+hbp batters in a no-hitter.  Using these guidelines, the probability of a no-hitter can be constructed into a calculable formula based on a starting pitcher’s on-base percentage, the probability of a walk, and the probability of a hit-by-pitch.  Later we will see that this probability can be reduced into a simpler and more intuitive formula.

Let h, bb, hbp be random variables for hits, walks, and hit-by-pitches and let P(H), P(BB), P(HBP) be their respective probabilities for a specific starting pitcher, such that OBP = P(H) + P(BB) + P(HBP).  The probability of a no-hitter or perfect game for a specific pitcher can be constructed from the following negative multinomial distribution (with proof included):

This formula easily reduces to the probability of a no-hitter by subtracting the probability of a perfect game:

The no-hitter probability may not be immediately intuitive, but we just need to make sense of the derived formula. Let’s first deconstruct what we do know… The no-hitter or perfect game probability is built from 27 consecutive “events” similar to how the perfect game probability is built from 27 consecutive outs.  These “event” and out probabilities can both broken down into a more rudimentary formulas. The out probability has the following basic derivation:

The “event” probability shares a comparable derivation that utilizes the derived out probability and the assumption that sacrifice flies are usually negligible per starting pitcher per season:

From this breakdown it becomes clear that the no-hitter (or perfect game) probability is logically constructed from 27 consecutive at bats that do not result in a hit, whose frequency we can calculate by using the batting average (BA). Recall that a walk, hit-by-pitch, or sacrifice fly does not count as an at bat, so we only need to account for hits in the no-hitter or perfect game probability. Hence, the batting average in conjunction with the on-base percentage, which does include walks and hit-by-pitches, will provide an accurate approximation of our original no-hitter probability:

Comparing the approximate no-hitter probabilities to their respective exact no-hitter probabilities in Table 2.2, we see that these approximations are indeed in the same ball park as their exact counterparts.

Table 2.2: No-Hitter Probabilities by Pitcher

The probability of a no-hitter is calculated for each pitcher (above) using their exact career on-base percentage, walk probability, and hit-by-pitch probability through the 2013 season.  Notice that the likelihood of throwing a no-no is significantly greater than that of a perfecto for each pitcher.  For example, Lincecum and Cain’s chances of making no-no history are far easier than being perfect by the respective factors of 15.9 and 11.5.  Although Lincecum and Cain are still both unlikely to accumulate the 1,231 and 1,055 starts necessary to ascertain these no-hitter probabilities.  If it’s any consolation, Lincecum already achieved his no-hitter by his 207th start (and another by his 236th start) and Cain already has a perfecto instead.

Furthermore, it’s possible for two pitchers with disparate perfect game probabilities to have very similar no-hitter probabilities, as we see with Sanchez and Bumgarner.  Sanchez has a no-hitter probability of 1 in 1,681 that is 56.2 times greater than his perfect game probability, while Bumgarner’s 1 in 1,772 probability is a mere 6.1 times greater.  This discrepancy can be attributed to Sanchez’ improved ability to not induce hits versus his tendency to walk batters, while Bumgarner’s improvement is of a lesser degree.  Regardless, Sanchez’ early no-hitter, achieved by his 54th start, can instill hope in Bumgarner to also beat the odds and join his 2010 rotation mates in the perfect game or no-hitter’s club.  Adding Bumgarner to the brotherhood would greatly support the claim that the Giants 2010 starting rotation was extraordinary.  However, the odds still fall in my favor that I will not need to rewrite this section of this study due to another unexpected no-no or perfecto by Lincecum, Cain, Sanchez, or Bumgarner.

The new prevailing trend in major league baseball is a disturbing one. It is a trend of exponentially more frequent Tommy John surgeries. During the surgery, the ulnar collateral ligament is replaced by a different tendon from elsewhere in the body. As would be predicted, pitchers suffer from the injury much more than batters because they are constantly stretching their arm to full extension and pitching at high velocities. However, there are times when batters must have their UCL repaired. The unfortunate truth is that there is little data on what may happen to batters when they return. Most analysts report that the surgery has little to no effect on batters’ performance. This isn’t true.

My search for answers began when I heard the news that Matt Wieters, the Baltimore Orioles catcher, would need to undergo Tommy John surgery. Suddenly, I realized that nobody really knows how he will fare when he returns next season. Same thing applies to Minnesota Twins’ top prospect Miguel Sano. Sano, the Twins’ powerful third baseman of the future, had to have his UCL replaced before the season began to the disappointment of prospect and Twins fans alike. The same kind of disappointment felt when Jose Fernandez needed to have Tommy John surgery. The injury is affecting more players at an exponential rate and there is little data (particularly in regards to batters) that suggests how it will affect them when they return.

I scoured the internet for the complete list of players who have undergone the procedure and came across a massive list of 737 confirmed players (major and minor leagues) and crossed out everyone that was not a position player. I was left with a meager list of 29 names from the major leagues (minor league players were excluded because of the distinct differences from each minor league level). After removing even more names of players who may have appeared briefly in the major leagues or had the surgery and never returned to playing, I was left with just 15 confirmed names. Stars of the times like Paul Molitor, one of the very first recipients of the surgery, and lesser known players like Kyle Blanks both stood out on the list.

The next step in the process of unraveling the mystery behind the surgery was to figure out how the surgery affects the batters. In other words, I wanted to test if different tools were affected and in what ways. Did batters hit for the same amount of power as they did before? To begin, I collected data to test for three different measures of arm strength. Batting Average on Balls in Play (BABIP) determines the rate at which balls put into play are turned into hits. While this is not entirely based on arm strength, arm strength is a large factor in placement of the ball coming off the bat. A more powerful swing will lead to more balls in play being turned into hits. More on that here. Slugging percentage (SLG) was the next piece of data I tested for. If a batter could hit the ball further, then they could have more extra-base hits. Similarly, I tested for Home Run to Fly Ball percentage (HR/FB). This measures the rate at which fly balls go over the outfield walls and become home runs. Another barrier to success, as can be seen in the image below, was that there was no recorded advanced fielding data prior to 2002. So it is possible that the HR/FB data is less diluted by sample size than the other measures.

Honestly, the results were surprising. Like most analysts, I believed that they would be right in saying that the surgery has little to no effect on batter strength. I found this to be wrong though because, on average, most batters did experience a non-negligible decrease in BABIP, SLG, and HR/FB.

Let’s face it: we’re all nerds here at FanGraphs. But it takes a special kind of nerd to bring FanGraphs’ brand of sabermetric analysis to that other realm of the dull and dweeby: the United States Congress.

Every summer, a handful of the 535 senators and congressmen who represent you in Washington divide into teams to play the Congressional Baseball Game, a charity event at Nationals Park. Despite its informal nature and the, ah, senescent quality of play, the game is a serious affair (something its participants often have experience with). This is no friendly softball game; the teams practice for months before the big day, and the players take the results very seriously.

So seriously, in fact, that players keep track of (even send press releases about) their hits and RBI. A small group of baseball-obsessed politicos scores and generates a box score for the game every year. With their help, I was able to take their record-keeping to the next level. This is where this becomes the dorkiest FanGraphs article ever—for the first time, we now have advanced metrics on the performance and value of U.S. congressmen’s baseball skills.

Using recent Congressional Baseball Game scoresheets, I made a Google spreadsheet that should look familiar to any FanGraphs user—complete with the full Standard, Advanced, and Value sections you see on every player page. (Though this spreadsheet is more akin to the leaderboards—since the game is only played once a year, I treated the entire, decades-long series as one “season,” and each line is a player’s career stats in the CBG.) From Rand Paul’s wOBA to Joe Baca’s FIP-, all stats are defined as they are in the Library and calculated as FanGraphs does for real MLBers—making this the definitive source for the small but vocal SABR-cum-CBG community.

That said, unfortunately the metrics can never be complete—there’s just too much data we don’t have. Most notably, although the CBG has a long history (dating back to 1909), I capped myself at stats from the past four years only—so standard small-sample-size caveats apply. (This is mostly for fun, anyway.) Batted-ball data is also incomplete, so I opted to leave it out entirely—and we don’t have enough information about the context of each at-bat to calculate win probabilities. For obvious reasons, there’s also no PITCHf/x data, and fielding stats are a rabbit hole I’m not even going to try to go down.

It’s still a good deal of info, though, and there’s plenty to pick through that goes beyond what you might have noticed with the naked eye at the past four Congressional Baseball Games. But why should I care to pick through them, you might ask; what good are sabermetrics for a friendly game between middle-aged men? Well, apart from the always-fun Hall of Fame arguments, they serve the same purpose they do in the majors: they help us understand the game, and they can help us predict who will win when the Democrats next meet the Republicans (how else would the teams be divided?) on the battle diamond—this Wednesday, June 25.

You probably don’t need advanced metrics to guess that the Democrats are favored. They’ve won the past five games in a row, including the four in our spreadsheet by a combined score of 61 to 12. That’s going to skew our data, but by the same token, Democratic players have clearly been better in recent years. Going by WAR, a full five Democrats are better than the best Republican player, John Shimkus of Illinois.

But the reason we expect Democrats to win on Wednesday is the player who tops that list: Congressman Cedric Richmond of Louisiana. Richmond’s 1.1 WAR (in only three games!) is 0.9 higher than the next-best player (Colorado’s Jared Polis), putting him in a league of his own. In each of the past three CBGs, the former Morehouse College varsity ballplayer has pitched complete-game gems that have stifled the Republican offense. He carries a 40.0% K% and 28 ERA- into this year’s game. (Note: Congressional Baseball Games last only seven innings, so the appropriate pitching stats use 7 as their innings/game constant in place of MLB’s 9.)

The GOP has a few options to oppose Richmond on the mound—it’s just that none of them are good. The four Republicans on the roster with pitching experience have past ERAs ranging from 8.08 to 15.75. If there’s any silver lining, it’s that Republican pitchers have been somewhat unlucky. Marlin Stutzman has a .500 BABIP, and Shimkus has an improbably low 20.8% LOB percentage. Thanks to a solid 15.0% K-BB%, Stutzman has just a 5.98 FIP—high by major-league standards, but actually exactly average (a FIP- of 100) in the high-scoring environment of the CBG. (Another note: xFIP is useless in the congressional baseball world, as no one has hit an outside-the-park home run since 1997.) A piece of advice to GOP manager Joe Barton of Texas: Stutzman is your best option for limiting the damage on Wednesday.

On offense, it’s again the Cedric Richmond show. His 8 wRC and 4.6 wRAA dwarf all other players. In a league where power is almost nonexistent, he carries a .364 ISO (his full batting line is a fun .818/.833/1.182); only eight other active players even have an ISO higher than .000. Other offensive standouts for the Democrats include Florida’s Patrick Murphy, he of the 214 wRC+ and .708 wOBA (using 2012 coefficients), and Missouri’s Lacy Clay, who excels on the basepaths to the tune of a league-high 0.5 wSB. With a 1.4 RAR (fourth-best in the league) despite only two career plate appearances, Clay has proven to be the best of the CBG’s many designated pinch-runners who proliferate in the later innings. (Caveat: UBR is another of those statistics we just don’t have enough information to calculate.) Democrats might want to consider starting him over Connecticut Senator Chris Murphy, however; Murphy is a fixture at catcher for the blue team despite a career .080 wOBA and -2.5 wRAA.

As on the mound, Republicans don’t have a lot of talent at the plate. Their best hitter is probably new Majority Whip Steve Scalise, who has a 168 wRC+, albeit in just four plate appearances. (Scouting reports actually indicate that Florida Rep. Ron DeSantis is actually their best player, but injury problems have kept him from making an in-game impact so far in his career—and he’s missing this game entirely due to a shoulder injury.) Meanwhile, uninspired performers like Jeff Flake (.268 wOBA) and Kevin Brady (.263 wOBA) continue to anchor the GOP lineup, potentially (rightfully?) putting their manager on the hot seat. Some free advice for the Republicans: try to work the walk better. Low OBPs are an issue up and down the lineup, and they have a .279 OBP as a team. Their team walk rate of 8.2% is also too low for what is essentially a glorified beer league. If someone is telling them that the way to succeed against a pitcher of Richmond’s caliber is to be aggressive, they should look at the numbers and rethink.