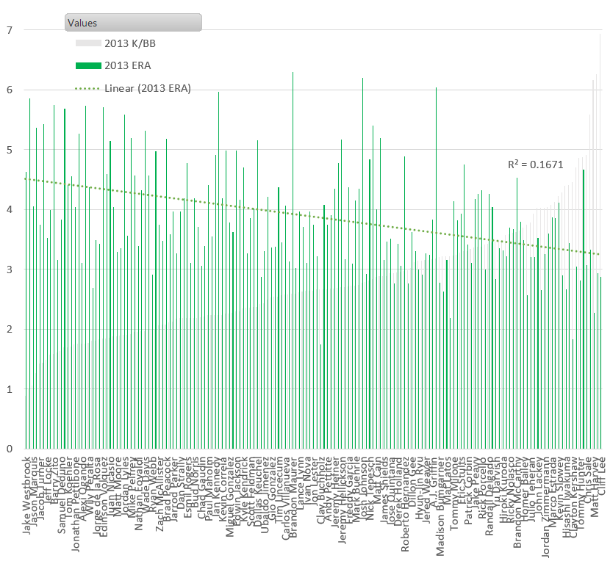
Top 5 Fantasy Starting Pitching Prospects for 2016
For this list there will be two requirements:
- The players under consideration must not have thrown even a single pitch in the major leagues. This throws out notable names such as Steven Matz, Jon Gray, and others who have already done so.
- The players under consideration must be projected to graduate from the prospect label in 2016 and have a significant influence on a major-league team. This throws out notable names like Julio Urias, Lucas Giolito, and others who are projected to be unlikely call-ups for the 2016 season.
So here we go, my projections for the top five pitching prospects you should keep an eye on for your fantasy team in 2016.
1. Tyler Glasnow
Team: Pittsburgh Pirates
Throws: Right
Height/Weight: 6’8”/225
Age: 22
Projected Path: Opening day rotation
Rundown: Nobody in this year’s projected rookie class boasts a bigger frame or, more importantly, a bigger fastball than Glasnow. Standing at an intimidating 6’8”, Glasnow is known to be able to pound the catcher’s mitt repeatedly with an upper 90s fastball that routinely overpowers hitters. MLB.com gives his fastball a 75 on the 20 to 80 scale, a truly remarkable grade. Add that to an above-average power curveball and an improving changeup, and it is easy to see why scouts rave about this guy’s immense upside.
But really, who cares about what scouts think? Not me, and neither should you. Let’s check out some upper-minor-league numbers Glasnow produced in 2015. Glasnow’s largest body of work in 2015 came in AA where he threw an even 63 innings over a span of 12 starts. Here he struck out a remarkable 33.1% of batters while only walking a respectable rate of 7.7% of batters he faced. His strikeout rate was tied with fellow highly-touted right-hander Jose De Leon for tops in all AA leagues among pitchers who threw at least 60 innings. Throw in his respectable walk rate, and he led all AA pitchers with the same inning restrictions in K-BB%. In AA he had an ERA of 2.43 while only stranding 66.4% of baserunners, a statistic generally attributed to luck. Again the average LOB% from 2015 was 72.3%, so one can assume he was a little unfortunate giving up some of those runs. With that said, his ERA could have easily looked more like his FIP which was an outstanding 1.98.
Either way, Glasnow proved to be dominant in AA and was later called up to the next level. In 43 innings of AAA ball he struck out a similarly great 27.6% of hitters. He walked some extra guys, leading to a high 12.6% BB%. Unsurprisingly, he was able to strand more runners in AAA, 73.3% of them to be exact, and yielded a 2.20 ERA. His FIP was 2.82.
Final take: Go get this guy. If he’s available late for a cheap price, Glasnow could be the ultimate diamond found in the rough. His best strength is in his strikeout numbers which plays really well for fantasy. The only weakness to his game is the walks. If he can find a way to limit walk totals, Glasnow could join the conversation for top young arms in 2016 and beyond.
2. Jose Berrios
Team: Minnesota Twins
Throws: Right
Height/Weight: 6’0”/190
Age: 21
Projected Path: Opening day rotation
Rundown: Perhaps more polished than Glasnow, Jose Berrios is a very strong name to have on your radar. As an undersized righty, Berrios hits mid-90s with his fastball, but will mainly live in the lower 90 range. He also throws a slurve-like breaking ball with various velocities as well as an above-average changeup. The best thing about Berrios is his plus command. As a 21 year old, he walked only 6.5% and 4.7% of batters in 90⅔ innings in AA and 75⅔ innings in AAA respectively. His strikeout numbers were also strong with a 25.1% mark in AA and a 27.7% effort in AAA. An interesting note on Berrios was his major improvement from AA to AAA. His K-BB% improved by 4.5%, as well as his FIP and ERA numbers.
Final Take: I was going back and forth for quite sometime trying to decide who was more valuable between Berrios and Glasnow. In the end I chose Glasnow mainly due to the unprecedented strikeout potential as well as the national league benefit. However, that by no means says that Berrios can’t be better. Led by his impressive ability to limit walks, go into your draft with Berrios’ name in mind.
3. Blake Snell
Team: Tampa Bay Rays
Throws: Left
Height/Weight: 6’4”/180
Age: 23
Projected Path: Opening day rotation
Rundown: Blake Snell is one of the most intriguing names in the prospect heap for 2016, partly because he came into the year as a relatively unknown 22-year-old in the Tampa Bays Rays A+ affiliate. The other part is that in 2015 he didn’t let up a run until his 50th inning of work. He escaped A+ ball in 21 innings without letting up a run and then rattled off another 28 scoreless innings in AA. Eventually though, he did prove to be human as he let up a first-inning home run to the Cubs’ Wilson Contreras ending his scoreless inning streak at 49. Nevertheless, he put up astounding numbers across three levels of the minor leagues in 2015.
Like Glasnow, Snell’s best tool is his ability to strike hitters out. He does this with a low to mid-90s fastball as well as an above-average slider and changeup. His biggest flaw is the walks, as he walked over 10% of the batters he faced in both AA and AAA. Like Berrios, he posted his best K-BB% numbers in AAA. In 44⅓ there he struck out 33.3% of batters and only walked 7.6%, good for an incredible 25.7% K-B%. Although it is very difficult to project his basic run-prevention skill without the aid of batted-ball type or velocity, he certainly excelled in that area in 2015. In 21, 68⅔, and 44⅓ innings in A+, AA, and AAA his ERA was 0.00, 1.57 and 1.83 respectively.
Final Take: Like I said at the beginning, Blake Snell is intriguing. Walks will hold him down, strikeouts will bring him up. If you like what see take a shot and thank me later. He has the potential of an elite starter.
4. Jose De Leon
Team: Los Angeles Dodgers
Throws: Right
Height/Weight: 6’2”/185
Age: 23
Projected Path: Mid/late season call up
Rundown: The only thing holding De Leon back from being closer to the top of this list is the Dodgers’ management. Most likely, he will not make the team out of camp and will head to AAA to start the year. However, due to the Dodgers’ thin staff and postseason desperation, De Leon is bound to make a splash sometime in 2016. As mentioned earlier, he was tied with Tyler Glasnow in K% in AA during the 2015 season among pitchers with more than 60 innings pitched. De Leon pitched a total of 76⅔ innings at the AA level through 16 starts. Before that, also in 2015, he threw 37⅔ innings at the A+ level. He put up ridiculous numbers there, striking out batters at a rate of a nearly unheard of 40% while only walking 5.4% of hitters. His walk rate increased a little bit in AA, but he still boasts better command than the likes of Glasnow and Snell. De Leon pairs his low to mid-90s fastball with a slider and changeup.
Final Take: Although De Leon is unlikely to make the team out of spring camp it is worth keeping this guy on your fantasy radar. Pay attention for any news on a potential call-up, and if you find any, don’t waste time to add him to your roster. In deeper formats, De Leon certainly deserves a late-round draft choice.
5. Josh Hader
Team: Milwaukee Brewers
Throws: Left
Height/Weight: 6’3”/160
Age: 21
Projected Path: Mid/late season call up
Rundown: After coming to the Brewers in the Carlos Gomez deal, Hader quickly improved his prospect stock by increasing his K-BB% by almost 10% with the move from the Astros AA affiliate to the AA affiliate of the Brew Crew. Although he started his only 7 games with Milwaukee, Hader spent time both starting and coming out of the pen before the deal in Houston. Over there he was not nearly as impressive with a higher BB% as well as significantly lower K% in 65⅓ innings. Like I promised, things got better in his 38⅔ innings for the Brewers in AA. Hader struck out a robust 32.9% of hitters while only walking 7.2%. Overall, Hader finished sixth in K-BB% among starters under 25 in AA who logged more than 60 innings. Hader pairs his mid-90s fastball with an average changeup and curveball. Due to his shot forward with the Brewers, and the lack of organizational pitching skill combined with likely trades of veterans either during the offseason or before the July trade deadline, Hader could be looking at a potential midseason call-up where his ability to get strikeouts would be an asset, especially in the NL. On top of this, Hader has better command than most 21-year-olds.
Final Take: Hader’s upside is real. A strong fastball, paired with above-average command bodes well for National League pitchers. Now all he has to do is continue his success in the minor leagues for the Brewers, and he will almost certainly see a call-up to the big-league rotation. If this happens make sure you remembered his name.
If you enjoyed this article be sure to check out our website www.analyticfb.com and our instagram @fantasybaseballanalytics!
Stats and research courtesy of FanGraphs and MLB.com
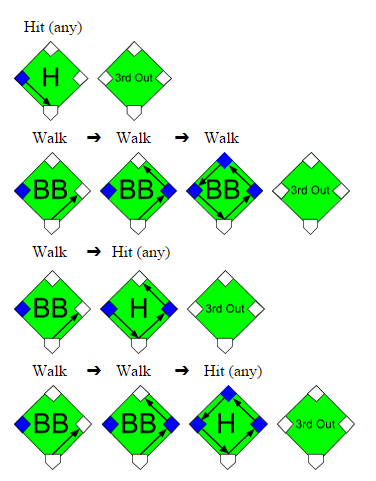
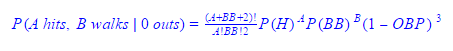
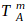 be a random variable for the total batters faced when he allows his mth hit; similarly, let b be P(H) for 2014 Bumgarner and
be a random variable for the total batters faced when he allows his mth hit; similarly, let b be P(H) for 2014 Bumgarner and  be a random variable for the total batters faced when he allows his 1st hit. If 2010 Pitcher A allows his mth hit on the jth batter, he will have a combination of m hits and (j-m) non-hits (outs, walks, sacrifice flies, hit-by-pitches) with the respective probabilities of a and (1-a); meanwhile 2014 Bumgarner will eventually allow his 1st hit on the (j+1)th batter or later and he will have 1 hit and the rest non-hits with the respective probabilities of b and (1-b). We can then sum each jth scenario together for any number of potential batters faced (all j≥m) to create the formula below:
be a random variable for the total batters faced when he allows his 1st hit. If 2010 Pitcher A allows his mth hit on the jth batter, he will have a combination of m hits and (j-m) non-hits (outs, walks, sacrifice flies, hit-by-pitches) with the respective probabilities of a and (1-a); meanwhile 2014 Bumgarner will eventually allow his 1st hit on the (j+1)th batter or later and he will have 1 hit and the rest non-hits with the respective probabilities of b and (1-b). We can then sum each jth scenario together for any number of potential batters faced (all j≥m) to create the formula below:

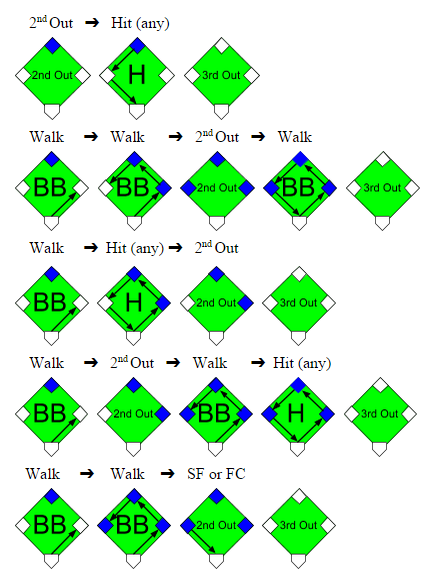
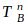 be a random variable for the total batters faced when 2014 Bumgarner allows his nth hit and
be a random variable for the total batters faced when 2014 Bumgarner allows his nth hit and 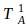 for when 2010 Pitcher A allows his 1st hit. However, instead of directly deducing the probability that 2010 Pitcher A allows 1 hit before 2014 Bumgarner allows his nth hit, we’ll do so indirectly by taking the complement of both the probability that 2014 Bumgarner allows his nth hit before 2010 Pitcher A allows his 1st hit (a variation of our first formula) and the probability that 2014 Bumgarner allows his nth hit and 2010 Pitcher A allows his 1st hit after the same number of batters.
for when 2010 Pitcher A allows his 1st hit. However, instead of directly deducing the probability that 2010 Pitcher A allows 1 hit before 2014 Bumgarner allows his nth hit, we’ll do so indirectly by taking the complement of both the probability that 2014 Bumgarner allows his nth hit before 2010 Pitcher A allows his 1st hit (a variation of our first formula) and the probability that 2014 Bumgarner allows his nth hit and 2010 Pitcher A allows his 1st hit after the same number of batters.