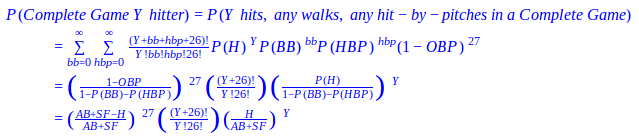Insurance in Baseball is Like a Black Hole
How much gravity does insurance have in Major League Baseball front office decisions?
Puns aside, let me tell you the funny thing about a black hole. You see astronomers cannot really see one, instead they are detected through their effects on the universe around them. Although less extreme, insurance is similar in this regard on its impact on baseball teams. Most teams insure some of their larger contracts in case their players cannot play due to an exterior factor such as injury. Perhaps the impacts of this major facet of the game does not cross our mind often because it is not eminently visible. However, make no mistake that insurance is a major factor when teams make major decisions regarding the DL, contract extensions, playing time and so on.
First, consider the history of baseball insurance to better understand why it impacts baseball. It can be said that by the late 1990s it had become common place for teams to insure their larger contracts. The first time baseball and insurance first truly started getting media attention was with Albert Belle in 2001 due to confusion over his insurance contract. Albert Belle had suffered a career-ending hip injury with the Orioles. Fans grew excited however despite the disheartening news when in 2002 the all-star slugger was added back onto the Orioles’ 40 man roster. Disappointed Orioles fans can tell you that Belle never played another MLB game however. Instead, he was added back onto the 40-man roster so the Orioles could collect insurance on his contract (some MLB insurance contracts do not cover a player unless they remain on the 40-man roster). At the time the MLB insurance contract covered the remainder of the salary owed on Belle’s contract. According to writer Michael Branda, the Orioles recovered an astounding 27.3 million out of a 39-million-dollar loss represented by Belle’s injury. Since the huge losses on Belle’s contract in the early 2000s, insurers in baseball have become much more stringent with their underwriting in baseball contracts.
Belle was not the only reason for teams being more stringent with their underwriting. The associated risks with insuring a MLB player have increased. One reason is PEDs. The MLB really did not enforce its ban on PEDs up until the late 2000s, but now being caught using PEDs can result in a significant loss in playing time. According to MLB Trade Rumors a syndicate of the MLB, Ervin Santana a first-time offender was suspended for 80 games on April 3rd of 2015. Santana was expected to make 13.5 million dollars this season. Despite being suspended, the Minnesota Twins are expected to still have to pay half of Santana’s salary (only players caught for the second time or more for steroids lose most of their salary).
To account for this insurers enforce a 60 to 90 day deductible policy in order to shield themselves from these sort of losses as well as claims made for short-term injuries. In addition to the 90 day deductible insurance policies are typically term policies of about three years with an option for renewal after the conclusion of the contract. As a result, if a contract proves to incur severe losses the liabilities will be only in the short term. Obviously to further protect themselves insurers only cover players with no preexisting injuries and all players must be inspected by the insurer. Furthermore, with wide variability and unpredictability in player health an insurer can in a way readjust its rate every three years to better reflect the player’s risk of not playing.
These more stringent underwriting practices have influenced the game, oftentimes when deciding when to take a pitcher off of the DL. Adam Kilgore of the Washington Post explained it best when he talked about how in 2012 Stephen Strasburg was “shut down” during a playoff push for the Nationals due to potential health concerns. In this decision there appeared to be a delicate balance between contention and the considerations of the insurance company that would not have covered Strasburg if he had been injured due to these health concerns. It is not crazy to think that finances come into play when making a decision on baseball players. Jeff Moorad, a decision maker for the Padres explained that in 2010 Chris Young was eligible to come off the DL. The Padres ultimately chose to put Young back on the field but Moorad added, “the accounting department much preferred that he [had stayed] on the disabled list.”
Baseball insurance has grown steadily more expensive. Although it is difficult to ascertain how much a team actually spends on insurance it is clear that it can be a burden for smaller teams. For instance, the Arizona Diamondbacks’ rotation once featured the dominant starting pitcher Brandon Webb. Between 2006 and 2008 Brandon Webb made three all-star games and finished first, second and second respectively in Cy Young voting. In this span Webb also led the league in innings pitched once. In essence Webb was due for a large payday once his contract expired. However contract negotiations between Webb and the Diamondbacks hit a snag in June of 2008. Despite a track record as a durable starter, no insurance company was willing to write a policy for injury risk to the Diamondbacks hurler. The reason is because insurance companies refused to accept the risk of Webb injuring his arm or if they were willing to, they were going to charge exorbitant rates.
As a result, the Diamondbacks could not get an insurance contract that did not have an exclusion on arm, shoulder or elbow injuries, all vital and injury-prone body parts for pitchers. According to AZCentral, a news outlet that covers the Arizona Diamondbacks, due to Webb not being insurable the Diamondbacks broke off all contract negotiations. In the long run, this proved to be a smart move since ten months later after contract talks ceased Brandon Webb never pitched in the majors again due to injuries. The point of this is that not only is baseball insurance so expensive it can prove to be impractical, it shows that most insurers are unwilling to insure some pitchers. Walt Jocketty, the former general manager for the middle-market St. Louis Cardinals explained that insurance has “become so expensive that it’s a cost item we really have to look at when you put your payroll together.”
In addition to insurance contracts altering how teams manage their rosters they influence how teams treat their players. In essence there is a human side to these contracts. Consider Josh Hamilton who is in the middle of a massive five-year, 125-million-dollar contract with the Angels and who has been playing quite ineffectively relative to his salary. Josh Hamilton who recently suffered a relapse on his drug addiction before the 2015 season is a prime example of insurance influencing teams to treat their players in a way they hopefully normally would not. Despite being a repeat offender, an arbitrator chose not to suspend Hamilton for any period of time. What makes this story scandalous is the Angels’ seemingly acerbic response to this news. It appears that the Angels almost wanted Hamilton to be suspended to spare them the expense of his failed contract. Clearly the Angels have little incentive to help Hamilton recover from his addiction. Instead, it is in their interest to see that Hamilton never plays another game of baseball again because if he does not play for an extended period of time the Angels can potentially collect insurance and definitely reduce their payroll.
Insurance influences baseball more than many people may realize. When it comes to playing time, DL decisions and contract negotiations, insurance seems to be an integral piece in the decision-making process. For me though, part of what makes baseball great is the inherent competition of players, often with disregard to their own body (*cough* Adam Eaton *cough*). There is little harm of teams protecting themselves from the inherent risks of baseball players becoming injured. The risk is that insurance becomes an incentive for teams to make decisions that may be bad for the game, such as not playing players for financial gain. Let’s hope that ultimately, teams do not get engulfed into this black hole.

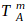 be a random variable for the total batters faced when he allows his mth hit; similarly, let b be P(H) for 2014 Bumgarner and
be a random variable for the total batters faced when he allows his mth hit; similarly, let b be P(H) for 2014 Bumgarner and  be a random variable for the total batters faced when he allows his 1st hit. If 2010 Pitcher A allows his mth hit on the jth batter, he will have a combination of m hits and (j-m) non-hits (outs, walks, sacrifice flies, hit-by-pitches) with the respective probabilities of a and (1-a); meanwhile 2014 Bumgarner will eventually allow his 1st hit on the (j+1)th batter or later and he will have 1 hit and the rest non-hits with the respective probabilities of b and (1-b). We can then sum each jth scenario together for any number of potential batters faced (all j≥m) to create the formula below:
be a random variable for the total batters faced when he allows his 1st hit. If 2010 Pitcher A allows his mth hit on the jth batter, he will have a combination of m hits and (j-m) non-hits (outs, walks, sacrifice flies, hit-by-pitches) with the respective probabilities of a and (1-a); meanwhile 2014 Bumgarner will eventually allow his 1st hit on the (j+1)th batter or later and he will have 1 hit and the rest non-hits with the respective probabilities of b and (1-b). We can then sum each jth scenario together for any number of potential batters faced (all j≥m) to create the formula below:

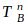 be a random variable for the total batters faced when 2014 Bumgarner allows his nth hit and
be a random variable for the total batters faced when 2014 Bumgarner allows his nth hit and 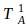 for when 2010 Pitcher A allows his 1st hit. However, instead of directly deducing the probability that 2010 Pitcher A allows 1 hit before 2014 Bumgarner allows his nth hit, we’ll do so indirectly by taking the complement of both the probability that 2014 Bumgarner allows his nth hit before 2010 Pitcher A allows his 1st hit (a variation of our first formula) and the probability that 2014 Bumgarner allows his nth hit and 2010 Pitcher A allows his 1st hit after the same number of batters.
for when 2010 Pitcher A allows his 1st hit. However, instead of directly deducing the probability that 2010 Pitcher A allows 1 hit before 2014 Bumgarner allows his nth hit, we’ll do so indirectly by taking the complement of both the probability that 2014 Bumgarner allows his nth hit before 2010 Pitcher A allows his 1st hit (a variation of our first formula) and the probability that 2014 Bumgarner allows his nth hit and 2010 Pitcher A allows his 1st hit after the same number of batters.