Introducing WPA-Win: A Better Pitcher Decision Statistic

Baseball fans have seen it time and again: a starting pitcher will twirl a masterpiece, but because his team doesn’t score, he’ll be tagged with a loss. Or a reliever will come into a game, pitch to one or two batters, and end up with the win.

The vagaries of assigning wins and losses to pitchers are a well-known irritant to serious baseball fans (though perhaps not to old-timers like Bob Costas or John Smoltz). Here is the pitching decision statistic explained:

The winning pitcher is defined as the pitcher who last pitched prior to the half-inning when the winning team took the lead for the last time.

The losing pitcher is the pitcher who allows the go-ahead run to reach base for a lead that the winning team never relinquishes.

Often timing — particularly the timing of a team’s offense — affects the statistic more than a pitcher’s actual contribution to his team’s win or loss. In other words, the decision frequently fails to reflect which pitcher made the biggest difference for the winning team (or was most detrimental for the losing team). In these cases, it simply tags the pitcher lucky or unlucky enough to pitch at a certain time in the game.

In an effort to create a more accurate stat to reflect a pitcher’s contribution to his team’s win or loss, I’d like to propose new stats, which I’ll call the “WPA-Win” and “WPA-Loss.” Let’s start with the WPA-Win:

The “WPA-Win” is given to the pitcher on the winning team with the highest WPA for that game.

I’ll address how to calculate the “WPA-Loss” (which is more complicated) later in the article. For now, we’ll just assume it goes to the pitcher on the losing team with the lowest WPA.

Before I defend this proposal, a quick explanation of WPA:

WPA (win probability added): WPA is the difference in win expectancy (WE) between the start of the play and the end of the play. That difference is then credited/debited to the batter and the pitcher. Over the course of the season, each players’ WPA for individual plays is added up to get his season total WPA.

Calculation Example: In game 4 of the 2007 World Series, the WE for the Rockies started out at 50%. When Jacoby Ellsbury doubled off Aaron Cook in the very first at-bat in the game, the Rockies WE declined to 44.2%. The difference or WPA was .058 wins (5.8%). Ellsbury was credited +.058 wins and Aaron Cook credited with -.058 wins.

Why you should care: WPA takes into account the importance of each situation in the game. A walk off home run is going to be weighted more than a home run in a game that has already gotten out of hand. This makes it a great tool for determining how valuable a player was to his team’s win total.

In each game a pitcher accumulates positive or negative WPA for each batter he faces, with the most important at-bats of the game given the most weight. Thus, in theory at least, the pitcher with the highest WPA did the most to help his team win.

Pitching a deGrom

Last year we saw a masterful season from Jacob deGrom, which culminated in a Cy Young Award… and a 10-9 record. Anyone who watched deGrom knew he was not an average pitcher, which, at least to the casual fan, is what a 10-9 record seems to suggest. But deGrom’s high number of losses were simply the latest example of something that’s happened countless times: a starting pitcher dominating for six or more innings, only to end up with a no-decision or even a loss because of a lack of run support. The purpose of the WPA-Win stat is to right those wrongs.

Let’s see the WPA-Win stat in practice. First, I’m going to look at a couple of historical examples from two past Opening Days from the Reds. It was these games that first led me to search for an alternative to traditional pitcher wins and losses.

April 4, 2016, Phillies vs. Reds (Reds win 6-2)

In this game, journeyman reliever Ross Ohlendorf got the W, even though he faced a grand total of one batter. That’s right, for having the good fortune to strike out Darin Ruf in the top of the 8th inning when the Reds were down 2-1 but were about to score five in the bottom half, he got declared the “winner” of the game. This despite starter Raisel Iglesias pitching six solid innings of two-run ball for the Reds.

But as you can see from the stat line above (far-right column), Iglesias totaled .10 WPA for the game, and Ohlendorf only totaled .03. (No other pitcher was above .08.) This fits with the narrative of the game — the bullpen was great, but Iglesias pitched well for two-thirds of the total innings, giving up only two runs. In this situation, Iglesias gets the WPA-Win, not Ohlendorf.

Now let’s go back to the Reds’ 2015 Opening Day:

April 6, 2015, Pirates vs. Reds (Reds win 5-2)

In this game, Johnny Cueto pitched seven marvelous innings, gave up no runs, struck out ten, and walked none. The Reds won 5-2 but Cueto didn’t get the W. Why not? Because Kevin Gregg blew the save in the first of many abysmal appearances for him in his brief stint with the Reds that year. Instead Jumbo Diaz, who faced one batter, got the W. Like Ohlendorf, Diaz lucked into pitching right before the Reds’ bats came alive (and after Gregg made a mess of things).

This game makes it even more clear which pitcher was most involved in the Reds’ win. Cueto easily amassed the highest WPA for Reds pitchers: .41. Diaz only had a .05 WPA. In this situation, Cueto gets the well-deserved WPA-Win.

So far our new WPA-Win stat looks to be working out. But what happens if two pitchers for the winning team tie for most WPA in a game? There are a number of possibilities for tie-breakers, such as the pitcher who pitched the most innings, or even falling back to the traditional “the pitcher who last pitched prior to the half-inning when the winning team took the lead for the last time.” Heck, you could even give each pitcher a half a WPA-Win — it’s not as if baseball stats are limited to whole numbers.

Because of the importance of a pitcher getting as many outs as possible, the first tiebreaker will be most innings pitched. And of course limiting runs is vital, so the second tiebreaker will be least runs scored when he is on the mound (i.e. earned, unearned, or inherited).

Rewarding Excellence

Now let’s take deGrom’s 2018 season as a case study to see how this new calculation impacts his record. I will also use it to explore how to calculate a “WPA-Loss” for a pitcher.

Using the traditional W/L method, deGrom was a pedestrian 10-9 in 32 starts. Using WPA-Win/Loss, he would have been 13-4. I think anyone would agree that the latter record is much more Cy Young-sounding and better reflects his dominance in 2018. In 24 of the 32 deGrom starts, both the traditional W/L and WPA-Win/Loss systems have the same result. This makes sense, as frequently the traditional W/L stat does reflect the pitcher who influenced the decision the most. But let’s look at a few examples from deGrom’s 2018 campaign; this will allow us to put the WPA-Win stat through the paces, as well as see how to calculate a WPA-Loss.

Rays at Mets, July 6, 2018 (Mets win 5-1)

In this game, deGrom pitched eight wonderful innings of one-run ball. His only blemish was giving up a home run to Willy Adames in the 5th inning. When deGrom left the game, the score was still tied, 1-1, as the Rays’ six-pitcher combination of Ryne Stanek, Ryan Yarbrough, Adam Kolarek, Diego Castillo, Jose Alvarado, and Chaz Roe also only allowed one run in eight innings (that seems about right: deGrom is equivalent to six Rays pitchers).

deGrom’s pitch count was 105 after eight, and so the Mets replaced him with Jeurys Familia to pitch in the ninth. Although Familia gave up a walk, a single, and hit someone with a pitch, he was able to get out of the jam and escape without giving up a run.

In the bottom of the ninth, the Mets loaded the bases and Jose Bautista hit a Grand Slam to walk off the Mets’ victory. Familia, being the pitcher of record at the time, got the win, and deGrom got a no-decision.

Now which Mets pitcher contributed more to the Mets’ win? deGrom, who gave up only one run in eight innings, or Familia, who pitched a single inning in relief? The answer is obvious, and the WPA-Win stat reflects that. deGrom had 0.35 WPA and Familia only 0.12. deGrom gets the WPA-Win here, instead of a no-decision.

Braves at Mets, August 3, 2018 (Braves win 2-1)

In this game, deGrom again pitched eight strong innings, this time giving up two runs. Unfortunately for deGrom (and predictably as well), the Mets only scored one run the whole game, giving deGrom the loss. Anthony Swarzak came on in the ninth for the Mets and pitched one shutout inning.

If we look at the WPA for each pitcher, deGrom ends up with 0.09 and Swarzak with 0.03. If we just flip the WPA-Win stat and give the WPA-Loss to the pitcher with the lowest WPA, then Swarzak gets the WPA-Loss. But that doesn’t seem right—what did Swarzak do wrong? He didn’t even give up a run!

In this case, the accumulation of WPA over eight innings vs. only one inning for Swarzak works in deGrom’s favor. And deGrom did pitch well — only allowing two runs in eight innings of work. When it comes to determining WPA-Wins, I think this is a feature, not a bug — the pitcher who pitches the most in a victory should be the one most likely to get the WPA-Win. But when it comes to a WPA-Loss, the same mechanism would penalize a reliever unfairly.

I think what stands out the most in this game is that Swarzak didn’t allow any runs — inherited or his own — to score while he was on the mound. In no situation should a pitcher get a WPA-Loss when that happens. So here’s my tweak:

The WPA-Loss is given to the pitcher on the losing team with the lowest WPA and who allowed at least one run (earned, unearned, or inherited) to score.

In this game, that means deGrom.

A quick note about “inherited” runs: In the traditional system of scoring, the pitcher who allows a runner to get on base is fully credited with the run if that runner scores, no matter if he is on the mound when it happens or not. I have always thought that is unfair to the pitcher. But since allowing an inherited runner to score can impact your own WPA, it can impact whether you get the WPA-Win or WPA-Loss.

Let’s now look at one more example, which shows how the WPA-Win/Loss stat preferences the starting pitcher, both for getting a win in a traditional no-decision situation, but also for getting a no-decision when he would otherwise get a traditional loss. As stated previously, this stat rewards a pitcher for more innings on the mound, which seems right to me.

Mets at Braves, June 13, 2018 (Braves win 2-0)

In a typical 2018 performance, this game featured seven innings of one-run ball from deGrom. Of course, the Mets didn’t score any runs, so he got the loss. Jerry Blevins pitched the eighth in this game for the Mets, also giving up one run. He got a no-decision, of course.

Looking more closely, however, deGrom accumulated 0.21 WPA while Blevins had -0.06 WPA. And in giving up a run, Blevins is eligible for the WPA-Loss; in fact, by having a lower WPA than deGrom, he receives the WPA-Loss.

This at first goes against our baseball instincts. After all, the starting pitcher gave up a run and his team didn’t score, so he should automatically be tagged with the loss according to traditional baseball accounting. But why? Why should deGrom’s one run count against him more than Blevins’s? After all, deGrom held the Braves to one run in seven innings, which surely kept the Mets in the game, while Blevins couldn’t even keep them scoreless for one inning.

Who did more to help his team win (and therefore prevent his team from losing) — the pitcher who pitched seven innings of one-run ball, or the one who gave up one run in one inning? The Mets were down 1-0 when Blevins entered the game in the bottom of the 8th, at which time they had an 87% chance of losing. But after facing just three batters, they had a 93% chance of losing. There is a big difference that late in the game between a 2-0 deficit and a 1-0 deficit. While timing is too influential in determining the traditional W/L stat, it isn’t altogether irrelevant. Therefore it makes sense for Blevins to get the WPA-Loss in this game instead of deGrom.

Examining deGrom’s 2018 season shows that the WPA-based system is much more useful than the traditional W/L system. And as we’ve seen, this case study does reveal something about the WPA-Win/Loss statistic: it favors starting pitchers for WPA-Wins, and “favors” relievers for WPA-Losses. This makes sense: someone who pitches more innings is helping his team more than someone who only pitches an inning (or even less), so favoritism towards the starters is justified.

In the final section of this article, I’ll sum up the WPA-Win/WPA-Loss statistic as well as look at the application of the stat in some extreme historical examples.

Righting Historical Wrongs

I have introduced a new way to calculate pitcher wins and losses based on the WPA he accumulates in a game: the WPA-Win/Loss statistic. I looked at a few past games as well as deGrom’s 2018 season to show the stat in action. Now I’d like to sum up as well as look at a couple exceptional historical games.

First, let’s fully define the WPA-Win/Loss statistic:

The “WPA-Win” is given to the pitcher on the winning team with the highest WPA in that game. In the case of a tie between two or more pitchers, the first tiebreaker is the most innings pitched, and the second tiebreaker is the fewest runs (earned, unearned, or inherited) allowed.

The “WPA-Loss” is given to the pitcher on the losing team with the lowest WPA in that game and who allows at least one run (earned, unearned, or inherited) to score. In the case of a tie between two or more pitchers, the first tiebreaker is the least innings pitched, and the second tiebreaker is the most runs (earned, unearned, or inherited) allowed.

This statistic is not perfect, but I believe it does a much better job of crediting the proper pitchers with wins and losses. There are a few objections I’d like to address.

First, some might argue that using WPA is too confusing for fans to follow. However, even though the traditional win statistic has been used for decades, I’d bet most casual fans don’t understand why Ohlendorf or Diaz received Opening Day W’s for facing just one batter. Also, baseball fans are getting more and more sophisticated when it comes to statistics: just a few years ago, OBP and SLG were considered esoteric stats for only the most die-hard stat-head, and now they are displayed on many broadcasts alongside more traditional stats. Finally, it would be easy for a broadcast to simply keep a running track of a pitcher’s WPA and display it on the screen at various times throughout the game.

Another possible objection is that the “pitcher decision” stat, no matter how it is determined, is nearly worthless. After all, wins and losses are team statistics, not individual ones. While this is a valid point, I would argue that pitcher wins and losses have been part of the game since the beginning, and they can — if properly calculated — reflect a pitcher’s enormous contribution to a team’s wins and losses. With that in mind, I would not want to throw out pitcher wins and losses entirely, but rather make them more meaningful.

Let’s check out two more past games to see if the WPA-Win/Loss system could right some historical wrongs (or if they would create any). Using Baseball Reference’s Play Index, I searched for games in which the losing pitcher amassed the highest WPA. (I also had to use links and images from Baseball-Reference for these games, since FanGraphs doesn’t list games before 1974).

Dodgers vs. Reds, September 15, 1941 (Dodgers win 5-1 in 17 innings)

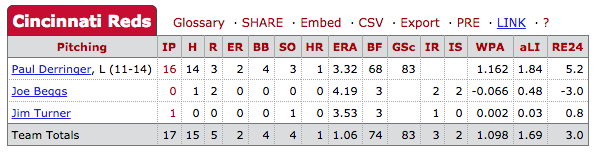
In this game, Paul Derringer pitched 16 (!) innings, giving up three runs. For this herculean effort, he was tagged with the L in spite of accumulating 1.162 WPA — tied for the highest ever for a losing pitcher. Looking more closely, we see that two runs were scored when Joe Beggs was on the mound — Derringer was taken out in the 17th inning after giving up a home run and two singles. Beggs allowed those two runners to score, and eventually he gave up two more of his own (both unearned), making it 5-0. The Reds scored one in the bottom of the 17th, but that wasn’t enough to save Derringer from being tagged with possibly the most unjust “L” in history. The WPA-Loss, on the other hand, would clearly go to Beggs, who had a -0.066 WPA for the game — a full 1.228 less than Derringer.

Next I wanted to see what winning pitcher had the lowest-ever WPA. Again, Play Index to the rescue:

Phillies vs. Braves, July 23, 1964 (Phillies win 13-10 in 10 innings)

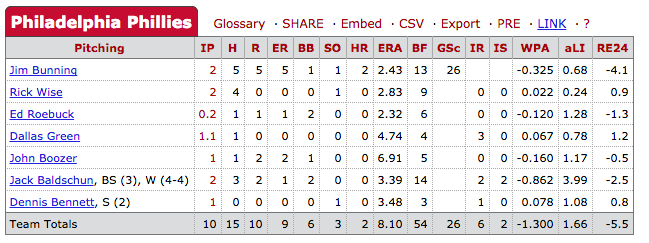
One of the worst infractions of the traditional win statistic occurs when a reliever blows a save and then ends up with the W. He is rewarded for failing to do his job — makes sense, right? This game is the most extreme example of that.

Hall of Famer Jim Bunning (future U.S. Senator from Kentucky) didn’t have a great start for the Phillies. He totaled -0.325 WPA by giving up five earned runs in two innings of work. Fortunately for him, his team was able to score a lot of runs that day. But look closer at the pitcher stats for the Phillies: Jack Baldschun, who totaled a staggering -0.862 WPA for the game, received the W for his “hard” work. How did that happen?

When Baldschun entered the game in the bottom of the 8th, the Phillies were winning 8-6 and there were two on with no one out. At this point, the Phillies had a 65% chance of winning. He quickly got the first batter out to increase the odds to 77%, but then the wheels fell off. By the time the inning was over, the score was 9-8 Braves and the Phillies only had a 15% chance of winning. He pitched another inning and gave up another run, for a total of four runs scoring on his watch.

However, it was Baldschun’s good fortune that the Phillies scored five runs while he was the pitcher of record, so by the traditional means, he was the “winner.” None of the Phillies pitchers that day were much to write home about, but the WPA-Win goes to Dennis Bennett, who closed the day for the winning team (in the WPA-Win/Loss system, a pitcher who gets the traditional “save” can also get the WPA-Win — but I consider the save stat close to useless, so that doesn’t really bother me).

These are the two most extreme cases of pitchers receiving ill-deserved decisions, and I’m sure there are many more out there. But in both cases, the WPA-Win/Loss statistic better reflects what actually happened.

I believe the WPA-Win/Loss statistic does a much better job of calculating pitcher wins and losses than the traditional system. I’ll continue to look at this way of calculating pitcher WPA-Wins and WPA-Losses to see if it has any major flaws or ways to improve it, but it is my hope that WPA-Wins and WPA-Losses give fans a more useful way to quickly see which pitcher most contributed to a team’s victory or loss.