Exploring Batter xwOBA and its Applications, Part 1

We are around the halfway point of the fourth season for which we have had Statcast data. One of the primary metrics created with Statcast data, introduced on the excellent Baseball Savant, is xwOBA (expected weighted on-base average), which I have noticed being adopted more for public analysis, including at this site.

The primary component of xwOBA is a statistical model that estimates the wOBA that each batted ball is expected to have produced based on its exit velocity and launch angle. In addition, actual strikeouts, walks, and times hit by a pitch are added in, as it is done in the normal wOBA formula.

There have been some explorations this year into the potential for predictive value added by xwOBA for pitchers, by Craig Edwards and Jonathan Judge, and batters, by Tom Tango and recent major leaguer Nate Freiman.

The pieces related to pitchers indicate what we would expect from our traditional DIPS principles: there is little evidence that pitchers have enough control over their results on balls in play to make including balls in play particularly worthwhile. For batter xwOBA, the pieces by Tom Tango and Nate Freiman serve as good jumping off points for a deeper dive, which is what I would like to present here (now that I’m finally done dragging my feet on writing this for a couple of months).

There is nothing too crazy presented here – think of this as a PSA on what batter xwOBA does, what goes into it, and why it is more of a stepping stone to future Statcast-based predictive metrics than something you should apply in a forward-looking manner today.

What does xwOBA do and what does that mean?

At the beginning of the article, I introduced the primary component of xwOBA as a statistical model that estimates wOBA for batted balls based on their exit velocity and launch angle. This more or less regresses the results of all batted balls to the mean wOBA we would expect of them without impact from or knowledge of the defense or park in which they were hit. In this way, it strips out a form of what could be called “BABIP luck” or “batted ball luck” that is associated with those things it does not include.

This is potentially powerful for predicting future performance, though it is not a predictive metric. In the case of batters, we know that they have substantially more control over their batted ball results than pitchers, generating a much wider range of BABIP and HR/FB% on a year-to-year or career basis than pitchers. Therefore, including analysis of balls in play for batters makes much more sense than for pitchers, which batter xwOBA could help to do.

However, while I have been seeing xwOBA regularly used to comment on early season breakouts or slumps, I have not come across a close look under the hood of batter xwOBA to both test its possible predictive capabilities and identify what sources of noise or “batted ball luck” it leaves in. Let’s see what we can find out.

What goes into xwOBA?

Statcast Quality of Contact Categories

To start, I decided to use some of the new “quality of contact” categories that the Statcast crew have defined. You’ve probably heard of barrels, the category that produces the highest wOBA (1.445, according to my calculations*), consisting generally of very hard hit fly balls and high line drives. It’s also the category seemingly most indicative of skill and thus signal amidst the noise, which is why it is the only one regularly used so far. The other five categories do contribute to xwOBA though, so let’s look at a quick summary of them.

*most of the numbers I use in here will be based on what I calculated using R from 2015-2017 Baseball Savant data, which may differ very slightly for a variety of reasons from what you see elsewhere – including, most likely, my personal failures. 

Statcast Quality of Contact Type Summary (2015-2017 data)

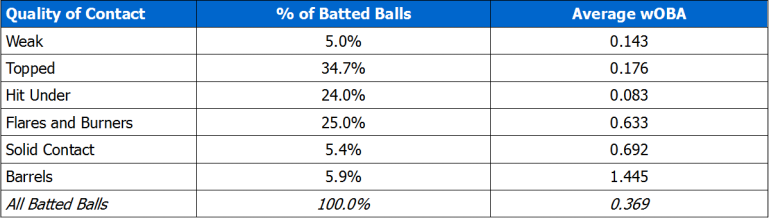
Some of those names are more self-explanatory than others – if you would like to know more specifics, here is a Tom Tango blog post explaining them as well as providing some visualizations to help.

Aside from the specifics of what each of the six quality of contact types refer to, the takeaway should be this: While barrels contribute the highest wOBA on average and are most representative of skill, well over 90% of batted balls are not barrels. Expected results on these non-barreled balls are still fed into the xwOBA model. For batters, how much less indicative of skill are these other batted balls? And if they are less indicative of skill, are they useful to include?

First, let’s simply look at how each quality of contact type correlates year-to-year. Unfortunately, we only have three full seasons of data to compare, but let’s do what we can. For players with at least 300 batted balls in each year, I calculated the year-to-year R² value for the rate at which players hit each quality of contact type. (e.g. 2015 Barrels/batted ball to 2016 Barrels/bb)

Year-to-Year R² of Statcast Quality of Contact Types

^Red denotes categories that produce poor batting results, green denotes good batting results

From the above table, we can get a sense of why the Statcast crew has focused on barrels – they are the only quality of contact type that produces both above average results and quite a bit of year-to-year reliability. Balls categorized as “topped” or “hit under” appear to approach barrels in reliability, but are worth very little. The “flares and burners” and “solid contact” categories produce close to half the value of barrels, but are far less reliable on a year-to-year basis.

For comparison, below are the year-to-year R² values for a few other things for the same set of hitters. Each of these metrics refer to the number of occurrences of that event per plate appearance.

Year-to-Year R² of Some “per PA” Metrics

This is pretty cool to me. Barrels per plate appearance or per batted ball seem to be in at least the same vicinity of year-to-year reliability as K% and BB%, which are two of the most important simple analysis tools out there for hitters. Barrel% is also a distinctive step above HR% in both sets of years compared.

But, what I really wanted to test going into this was smaller sample reliability, given the usage of xwOBA in so many early season articles.

In the following tables are R² values for the same quality of contact and per PA metrics we have discussed so far, but instead of looking at year-to-year R², we are testing the relationship between roughly the first third of a season (before June 1st) and the final two thirds of a season (June 1st onward).

R² Comparing Pre-June 1st to June 1st Onward – Statcast Quality of Contact Types

R² Comparing Pre-June 1st to June 1st Onward – Some “per PA” Metrics

Note: I simply proportionally adjusted my batted ball minimums for batters in this sample (batters with min. 100 bb before June 1st and min. 200 bb from June 1st onward), weirdly producing 149 batters in each year…

In general, of course, these R² values are a bit worse than the year-to-year ones. Strikeouts and barrels look the best here, with the next tier probably being topped, hit under, and walks.

What struck me most was something I figured I would find here: flares and burners take a significant hit in this smaller sample. How many flares and burners a player hits through a couple of months tells you very little about how many they will hit for the rest of the season.

To help visualize this, below are two graphs from the 2017 “pre-June 1st to June 1st onward” comparison: flares and burners per batted ball (R² = 0.11) and barrels per batted ball (R² = 0.64).

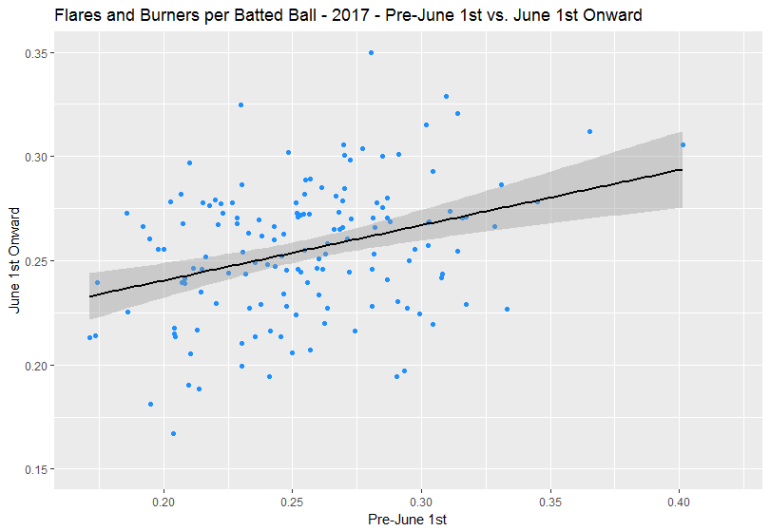
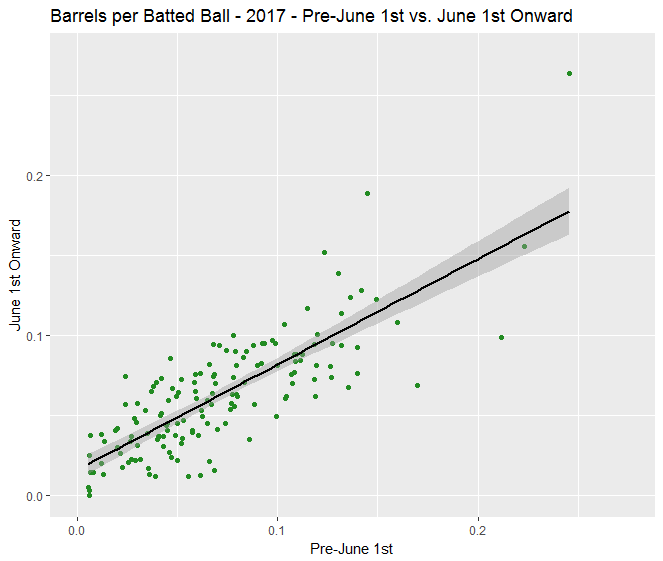
There is no doubt here that barrels are more indicative of a repeatable skill in partial season samples than flares and burners. (I want to say thanks to Aaron Judge for stretching out the barrels graph, by the way.)

This is why, earlier in the article, I said that xwOBA only strips out certain types of batted ball luck. In a small sample, players could hit some extra soft line drives, hard ground balls, or bloop singles instead of cans of corn or weak grounders, causing them to have an uncharacteristically high wOBA and xwOBA. Our analysis to this point deems knowing about those flares and burners to be not very useful for assessing a batter’s future results partway through a season.

But how much of an impact could that possibly have? Well, I calculated that flares and burners produced a .633 wOBA from 2015-2017 while making up about a quarter of all batted balls. According to FanGraphs, the highest wOBA ever recorded in a qualified batting season was .598 by Babe Ruth in 1920.

So yes, I think that lucking into some extra peak Babe Ruth plate appearances could have a relevant impact on a batter’s small sample xwOBA.

Up next

We have covered a lot so far, so I will break things here. In Part 2, we will look at a similar analysis on wOBA and xwOBA themselves, see if we can create a more simplistic metric than xwOBA that is comparably predictive in small samples, and discuss how the Statcast crew is likely working to create predictive metrics based on Statcast data (since that’s not what xwOBA is, making this analysis pretty unfair to them!).