Adam Wainwright pitched a decent game Monday night in Game 3 of the NLCS, throwing 7 innings and giving up 6 hits, no walks and striking out 5. He had a game score of 62, usually a sign of a well-pitched game, and he ended up with the loss because the Cardinals offense chose to take the night off. Brian Kenny (@MrBrianKenny) of the MLB Network started a movement called KillTheWin, his quixotic effort to have the win eliminated as a baseball statistic. I wrote a couple posts at my blog Beyond The Scorecard because I thought it was an interesting idea and seemed like a fun issue to research and will include the links at the end of this post, but Wainwright’s game got me thinking–how often in the postseason is a pitcher not justly rewarded for a good effort?

As the use of starting pitchers has changed over time, the win has become a far less effective metric in judging pitcher effectiveness. I don’t remember how I stumbled across using a game score of 60 as my marker of effectiveness (probably at Kenny’s suggestion) and like any other single number it’s not the entire story of a pitching performance, but it grants the opportunity to separate pitching effectiveness from a lack of offensive production or bad defense. Including Monday’s game there have been 1,393 postseason games played since 1903, meaning there have been 2,786 starts in postseason history–this chart shows the breakdown of wins, losses and no-decisions for those starters in that time frame:

In the postseason, starting pitchers won almost 36% of their starts. This covers the entire spectrum of postseason play, from the games in the early 1900s when a pitcher typically finished what he started all the way to examples like Saturday where Anibal Sanchez was removed after 6 innings (and 116 pitches)…and throwing a no-hitter. Different times, to be sure. With this context, this chart shows how often a pitcher who had a game score of 60 or greater was credited with the win:

Definitely an improvement over the general trend, but still, a pitcher who pitches well enough to attain a game score of 60 or greater has done all he can–he’s given up few hits and walks and struck out a decent number of hitters. In short, he’s kept base runners off base, the primary job of a pitcher and almost 35% of the time has nothing to show for it, or even worse, is tagged with a loss. This chart shows these numbers since the playoffs were expanded in 1969:

The introduction of relievers definitely hurt the cause of these starting pitchers, with almost 40% of pitchers who threw very good games not receiving a win. On the flip side, it is gratifying to see that only around 9% of wins go to pitchers who were the beneficiaries of being on the right side of 13-12 scores or games along those lines–justice exists somewhere. This last chart shows the record by game score stratification:

Who was that unlucky pitcher with a game score greater than 90 who received the loss? Nolan Ryan in Game 5 of the 1986 NLCS.

The 10-15 regular readers of my blog hopefully are aware that I typically write with my tongue firmly lodged in my cheek, and the win is so entrenched in baseball lore that removing it as a point of discussion simply won’t happen, but it doesn’t mean that it has to receive the emphasis it does. When we have the wealth of data that sites like FanGraphs places at our fingertips, we don’t have to rely on a metric that was formed at the inception of organized baseball that is a relic today, particularly one that doesn’t give an accurate portrayal of pitching performance around 35% of the time. Kill The Win–maybe not, but we can certainly de-emphasize it.

#KillTheWin blog posts:

The first one, which lays out definitions and rationale

The second one, which expands it

A final one, an exercise in absurdity

Talcott v. National Exhibition Co., 144 A.D. 337, 128 N.Y.S. 1059 (2 Dept., 1911)

What was Merkle’s Boner?

On September 23, 1908 the Chicago Cubs played the New York Giants at the famed Polo Grounds.  Al Bridwell came to bat with two outs and the game tied 1-1 in the bottom of the ninth.  He laced a single to the outfield and the runner on third trotted home, thinking he had just scored the winning run.  The Cubs second baseman Johnny Evers, of the famed “Tinkers to Evers to Chance” double play combination and future Hall of Fame inductee, however, called for the ball from the outfield because Fred Merkle, the Giants runner on first, had not touched second base.  Although there is controversy regarding whether Evers got the actual ball back, the umpire ruled Merkle out at second and due to the force, the apparent winning run was erased.

As was common at the time, the fans at the Polo Grounds would walk across the field after the game to exit the ballpark.  By the time the play was decided and the winning run nullified, however, the fans believing the Giants had won were already streaming across the field and it was impossible to resume the game before the game was called on account of darkness.

On October 6, 1908, the National League Board of Directors made its final ruling that because Merkle had failed to reach second, the force rule was applied correctly and the game was a tie.  At the end of the season, the Cubs and Giants were tied for first place and a makeup game was needed to determine which team would play in the World Series.  This game was played on October 8, 1908 at the Polo Grounds and reportedly drew 40,000 people, the largest crowd ever to have attended a single baseball game at the time.

The Cubs won this game over the Giants and went on to beat the Tigers 4-1 in the World Series, their last World Series victory.

The play that forced the makeup game was dubbed “Merkle’s Boner” and Fred Merkle was tagged with the nickname “Bonehead.”  Years later, Merkle admitted that he never touched second base but claimed he had been assured by umpire Bob Emslie that the Giants had won.  Despite a solid 16-year Major League career, including four seasons with the Cubs, Merkle was never able to shake the stigma of the play.

What does Merkle’s Boner have to do with this case?

As a result of the play and the October 6^th mandate for the makeup game, the Polo Grounds played host to the makeup game on October 8, 1908.  This game was “of very great importance to those interested in such games, and a vast outpouring of people were attracted to it.”  On the morning of the game, the ticket booths at the Polo Grounds were inundated with people trying to secure reserved seats for that afternoon’s game.

Plaintiff Fredrick Talcott, Jr. went to the ballpark intending to buy tickets for the game and entered an “inclosure” where the ticket booths were located.  After finding that the tickets were sold out, he tried to leave the inclosure along with a great number of people also trying to exit at the same time.  As he attempted to leave, however, ballpark attendants prevented his exit and he was “detained in the inclosure for an hour or more, much to his annoyance and personal inconvenience.”  Mr. Talcott brought this lawsuit seeking damages for false imprisonment.  He further claimed to have been pushed by the defendant’s “special policemen.”

The Giants countered that plaintiff simply could have used one of the other exits available.  Mr. Talcott alleged, however, that he was not aware of any other exits to the inclosure and none were pointed out to him.

Who won?

The case went to a jury trial and Mr. Talcott was awarded $500 in damages (approximately $12,000 today) with judgment entered on May 19, 1910.

The Giants appealed but the appellate court affirmed the judgment in favor of Mr. Talcott.

Why?

The jury found that that plaintiff’s detention was unwarranted.  The appellate court agreed with this finding, ruled that the award was not excessive and found no reason to interfere with the jury’s verdict.

Additionally, the court found that Mr. Talcott was not required to demonstrate that he incurred any special or actual damages as a result of the detention.

Pitch sequencing is a complicated topic of study. Given the previous pitch(es) to a batter, the next pitch may depend on factors such as the game-based information (e.g., count, number of outs, runners on base); the previous pitch(es), including their location, type, and batter’s response to them; and the scouting report against the batter as well as the repertoire of the pitcher. In order to approach pitch sequencing from an analytical prospective, we need to first simplify the problem. This may involve making several assumptions or just choosing a single dimension of the problem to work from. We will do the latter and focus only on the location of pitches at the front of the strike zone. Since we are interested in pitch sequencing, we will consider at-bats where at least two pitches were thrown to a given batter. The idea is to use this information to generate a simple model to indicate, given the previous pitch, where the next pitch might be located.

We can start with examining the distance between pitches, regardless of the location of the initial pitch. If this data, for a given pitcher, is plotted in a histogram, the spread of the data appears similar to a gamma distribution. Such a distribution can be characterized many ways, but for our purposes, we will use the version which utilizes parameters k and theta, where k is the shape parameter and theta is the scale parameter. With a collection of distances between pitches in hand, we can fit the data to a gamma distribution and estimate the values of k and theta. As an example, we have the histogram of C.J. Wilson’s distances between pitches within an at-bat from 2012 overlaid with the gamma distribution where the values of k and theta are chosen via maximum likelihood estimation.

Author’s note: I started working on this quite a few weeks ago and so, at the time, the last complete set of data available was 2012. So rather than redo all of the calculations and adjust the text, I decided to keep it as-is since the specific data set is not of great importance in explaining the method. I will include the 2013 data in certain areas, denoted by italics.

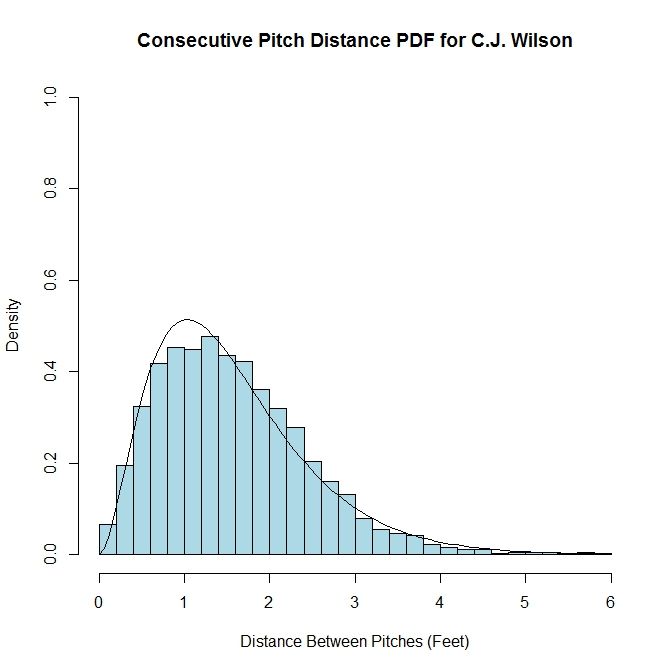
While this works for the data set as a whole, this distribution will not be too useful for estimating the location of a subsequent pitch, given an initial pitch. One might expect that for pitches in the middle of the strike zone, the distribution would be different than for pitches outside the strike zone. To take this into account, we can move from a one-dimensional model to a two-dimensional one. Also, instead of using pitch distance, we are going to use average pitch location, since this will include directional information as well. To start, we will divide the area at the front of the strike zone into a grid of three-inch by three-inch squares. We choose this discretization because the diameter of a baseball is approximately three inches and therefore seems to be a reasonable reference length. The domain we consider will be from the ground (zero feet) to six feet high, and three feet to the left and right of the center of home plate (from the catcher’s perspective).

We will refer to pairs of sequential pitches as the “first pitch” and the “second pitch”. The first pitch is one which has a pitch following it in a single at-bat. This serves as a reference point for the subsequent pitch, labeled as the “second pitch”. Adopting this terminology, we find all first pitches and assign them to the three-inch by three-inch square which they fall in on the grid. Then for each square, we take its first pitches and find the vector between them and their associated second pitches (each vector points from the first pitch to the second pitch). We then average the components of the vectors in each square to provide a general idea of where the next pitch in headed for the first pitches in that square.

In areas where the magnitude of the average vector is small, the location of the next pitch can be called isotropic, meaning there is no preferred direction. This is because average vectors of small magnitude are likely going to be the result of the cancellation of vectors of similar magnitude in all directions (from the histogram, the average distance between pitches was approximately 1.5 feet with most lying between 0.5 and 2.5 feet apart). One can create contrived examples where, say, all pitches are oriented either left or right and so there would be two preferred directions rather than isotropy, but these cases are unlikely to show up at locations with a reasonable amount of data, such as in the strike zone. In areas where the average vector has a large magnitude, the location of the next pitch can be called anisotropic, indicating there is some preferred direction(s). Here, the large magnitude of the average vector is due to the lack of cancellation in some direction. For illustrative purposes, we can look at one example of an isotropic location and one of an anisotropic location. First, for the isotropic case:

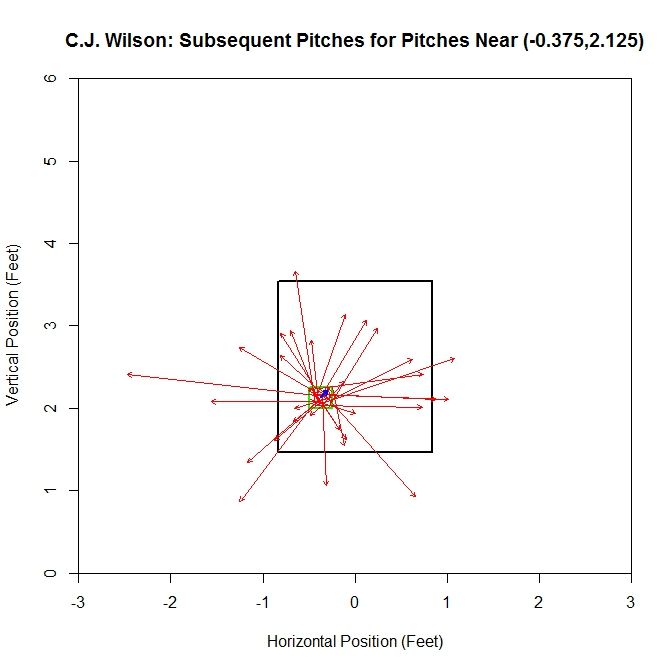
In this plot, the green outline indicates the square containing the first pitches and the red arrows are the vectors between the first and second pitches. The blue arrow in the center of the green square is the average vector. For the grid square centered at (-0.375,2.125), we have a fairly balanced, in terms of direction and distance, distribution of pitches. Therefore the average vector is small in magnitude. In other cases, we will have the pitches more heavily distributed in one direction, leading to an anisotropic location:

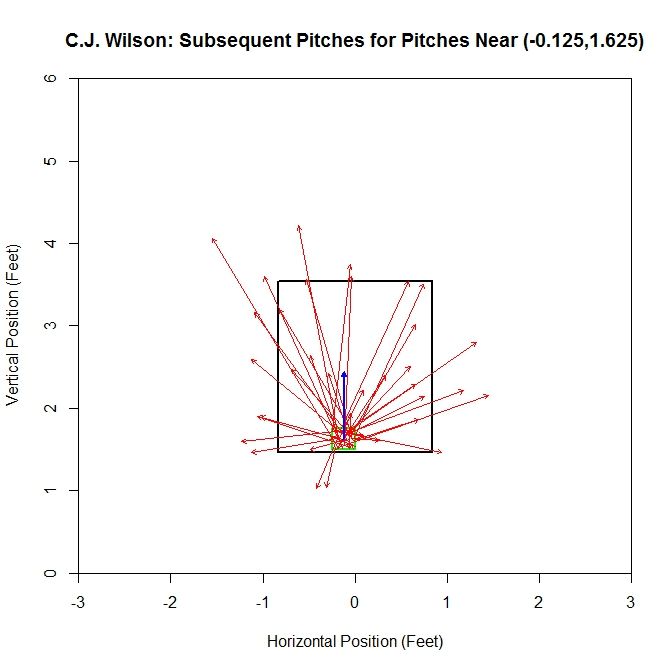
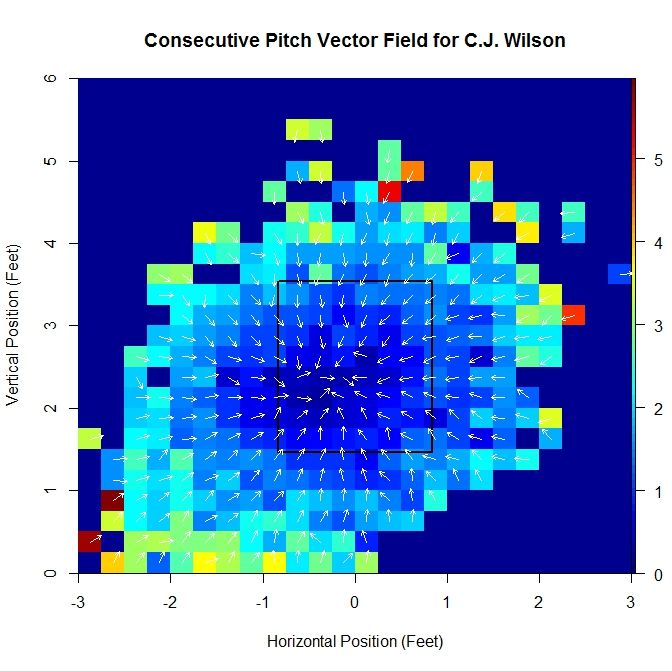
As opposed to the previous case, there is a distinct pattern of pitches up from the position (-0.125,1.625), which is shown by the average vector having a substantially larger magnitude. This is due to most of the vectors having a large positive vertical component. Running over the entire grid where at least one pitch had a pitch following it, we can generate a series of these average vectors, which make up a vector field. In order to make the vector field plot more legible, we remove the component of magnitude from the vector, normalizing them all to a standard length, and instead assign the length of the vector to a heat map which covers each grid square.

For the 2013 data set:

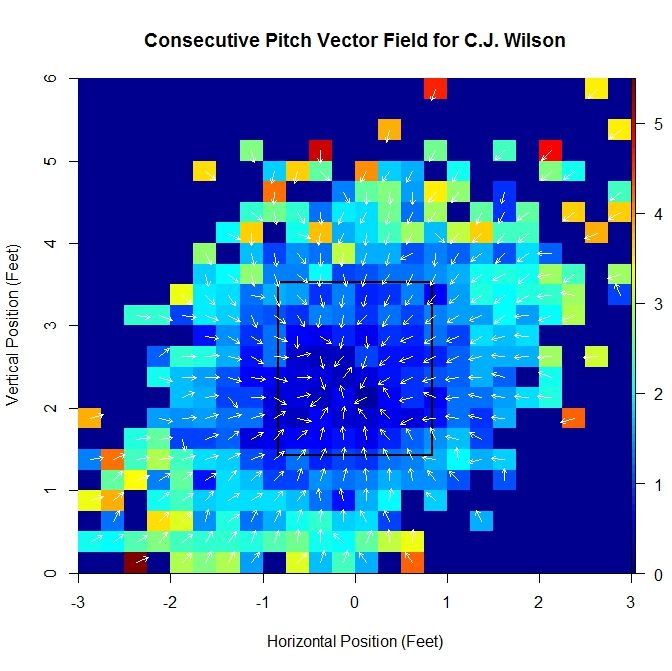
By computing these vectors over the domain, we are able to produce a vector field, albeit incomplete. Computing this vector field based on empirical data also lends itself to outliers influencing the average vectors as well as problems with small sample size. We can attempt to handle these issues and gain further insight by finding a continuous vector field to approximate it. To do this, we will begin with a function of two variables, to which we can apply the gradient operator to produce a gradient field. We can zoom in near the strike zone to get a better idea of what the data looks like in this area:

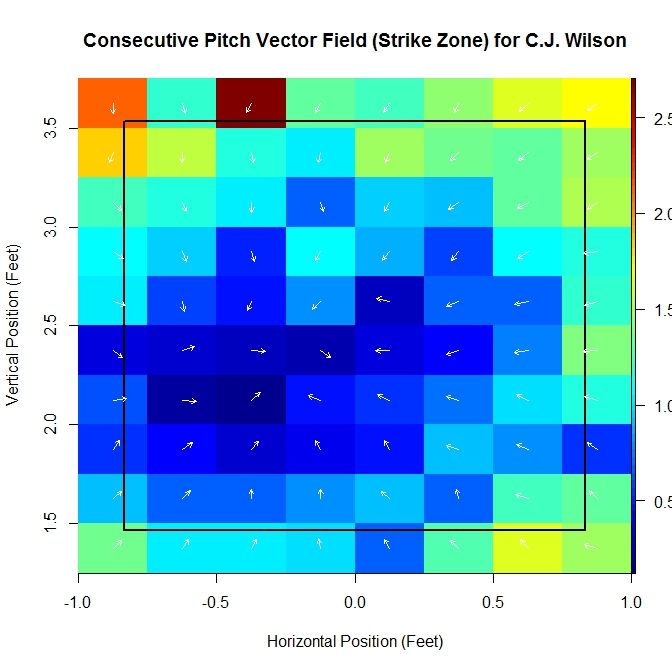
Note that as we move inward, toward the middle of the strike zone, the magnitude of the average vector shrinks. In addition, the direction of all vectors seems to be toward a central point in the strike zone. Based on these observations, we choose a function of the form

P(x,z) = (1/2)c_x(x – x_0)^2 + (1/2)c_z(z – z_0)^2.

The x-variable is the horizontal location, in feet, and z the vertical location. This choice of function has the property that there is a critical point for P and when the gradient field is calculated, all vectors will radially point toward or away from this critical point. The constants in the equation of this paraboloid are (x_0,z_0), the critical point (in our case, it will be a maximum), and (c_x,c_z) are, for our purposes, scaling constants (this will be clear once we take the gradient). The gradient of function P is

grad(P) = [c_x(x – x_0), c_z(z – z_0)].

Then c_x and c_z are constants that scale the distances from the x- and z-locations to the critical point to determine the vector associated with point (x,z). Note that grad(P)(x_0,z_0) = [0,0]. In fact, we will give this point a special name for future reference: the pitching sink. For vector fields, a non-mathematical description of a sink is a point where, locally, all vectors point toward (if one imagines these vectors to be velocities, then the sink would be the point where everything would flow into, hence the name). This point is, presumably, the location where we have the least information about the direction of the next pitch, since there is no preferred direction. Again using Wilson’s data as an example:

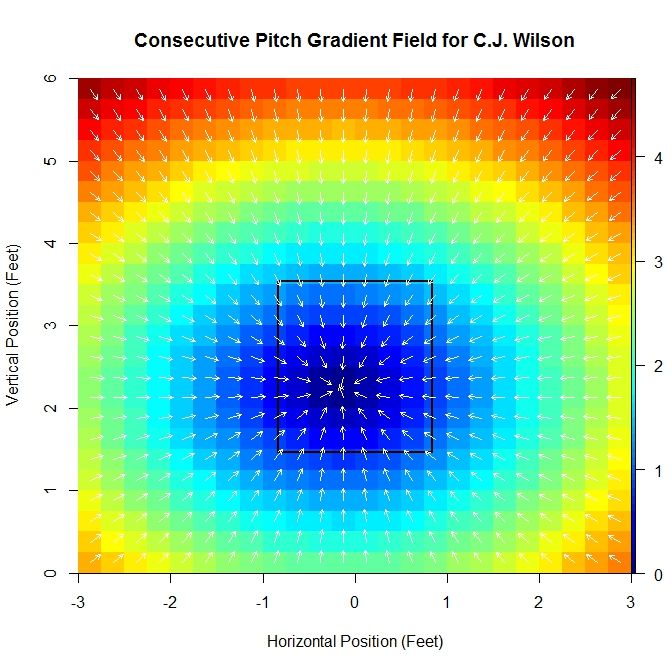
For the 2013 data set:

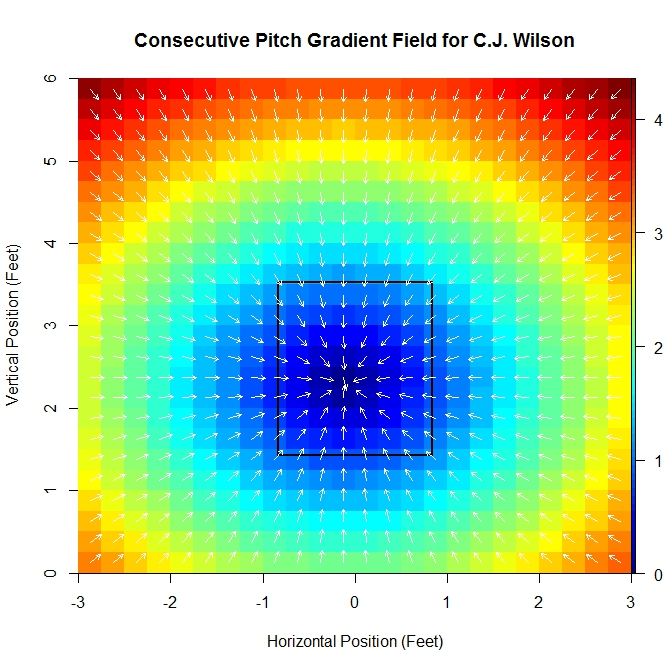
The gradient field is fit to the average vectors using linear least squares minimization for the x- and z-components. This produces estimates for c_x, c_z, x_0, and z_0. For the original vector field, if we are interested in the location where the average vector is smallest in magnitude (or the location where there is the least bias in terms of direction of the next pitch), we are limited by the fact that we are using a discretized domain and therefore can only have a minimum location at a small, finite number of points.

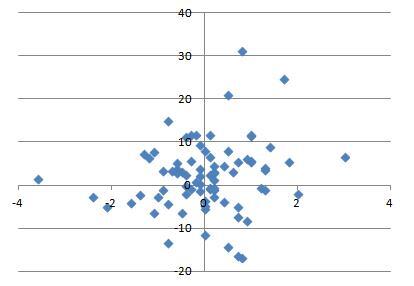
One advantage to this method is that it produces a minimum that comes from a continuous domain and so we will be able to get unique minimums for different pitchers. Another piece of information that can be gleaned from this approximation is the constants, c_x and c_z. If c_x is large in magnitude, there may be a large east-west dynamic to the pitcher’s subsequent pitch locations. For example, if a first pitch is in the left half of the strike zone, the next pitch may have a proclivity to be in the right half and vice versa. A similar statement can be made about c_z and north-south dynamics. Alternatively, if c_x is small in magnitude, then less information is available about the direction the next pitch will be headed. For Wilson, the constants obtained from the best fit approximation are a pitching sink of (-0.163,2.243) and scaling constants (-0.925,-1.055).

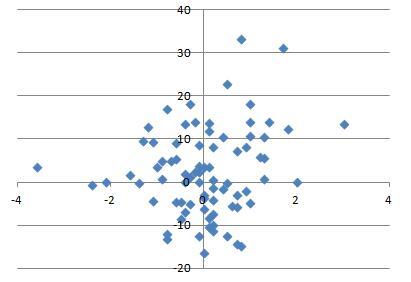
For C.J. Wilson’s 2013 season, we have the sink at (-0.109,2.307) and scaling constants (-0.902,-0.961), so the values are relatively close between these two seasons.

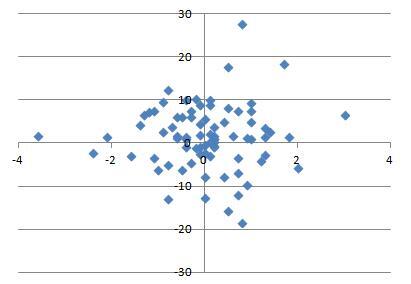
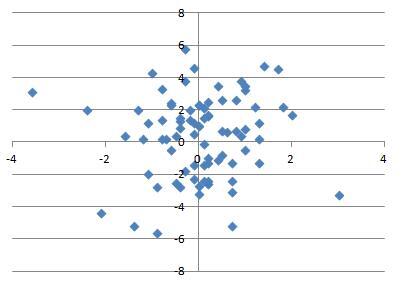
We can now obtain this set of parameters for a large collection of pitchers. For each pitcher, we can find the vector field based on the data and then find the associated gradient field approximation. We can then extract the scaling constants and the pitching sink. We can run this on the most recent complete season (2012, at the start of this research) for the 200 pitchers who threw the most pitches that year and look at the distribution of these parameters.

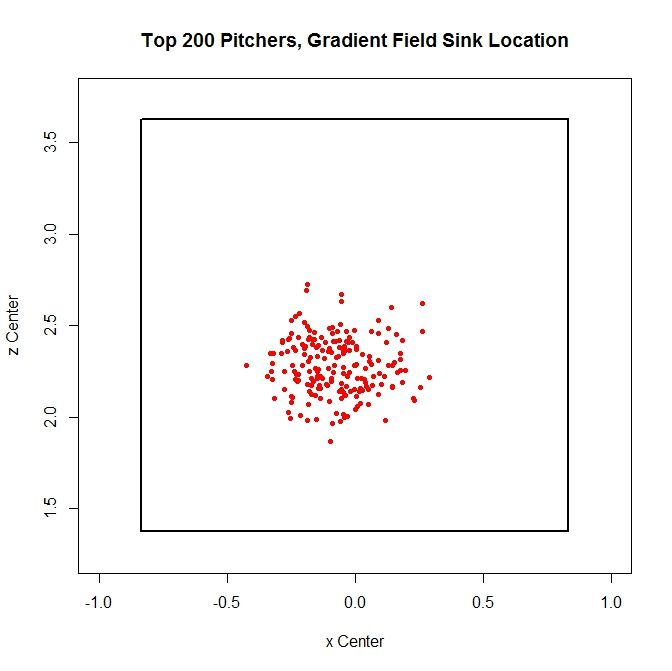
The sinks cluster in a region roughly between 1.75 and 2.75 feet vertically and -0.5 and 0.5 feet horizontally. This seems reasonable, since we would not expect this location to be near the edge or outside of the strike zone. Similarly, we can plot the scaling constants:

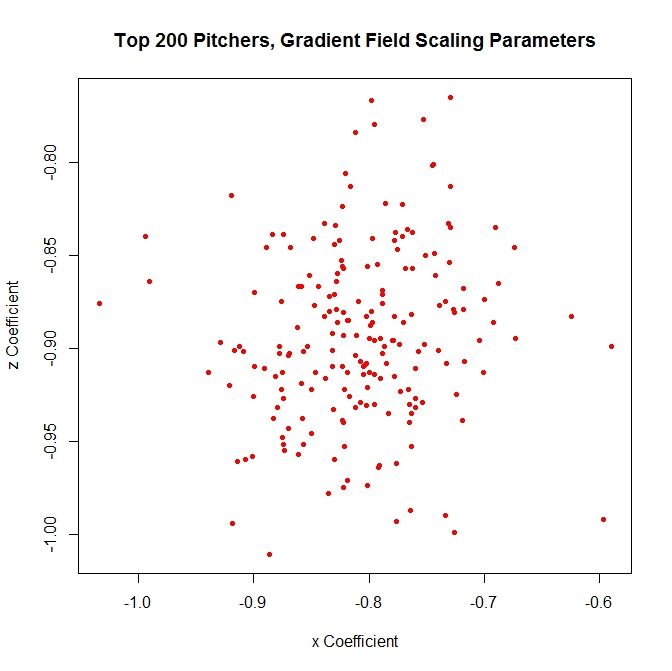
The scaling constants are distributed around a region of -1 to -0.8 vertically and -0.7 and -0.9 horizontally.

One problem that arises from this method is that since we are averaging the data, we are simplifying the analysis at the cost of losing information about the distribution of second pitches. Therefore, we can take a different approach to try to preserve that information. To do so, at a grid location, we can calculate several average vectors in different directions, instead of one, which will keep more of the original information from the data. This can be accomplished by dividing the area around a given square radially into eight slices and calculating the average in each octant.

However, since each nonempty square may contain anywhere from one to upwards of thirty plus pitches, using octants spreads the data too thin. To better populate the octants, we can find pitchers with similar data and add that to the sample. To do this, we will go back to the aforementioned average vectors and use them as a means of comparison. At a given square, with a pitcher in mind whose data we wish to add to, we can compute the average vector for a large collection of other pitchers, compare average vectors, and add the data from those pitchers whose vector is most similar to the pitcher of reference. In order to do this, we first need a metric. Luckily, we can borrow and adapt one available for comparing vector fields:

M(u,v) = w exp(-| ||u||-||v|| |) + (1-w) exp(-(1 – <u,v>/||u|| ||v||))

Here, u and v are vectors, and w is a weight for setting the importance of matching the vector magnitudes (left) and the vector directions (right). For the calculations to follow, we take w = 0.5. The term multiplied to w on the left is an exponential function where the argument is the negative of the absolute value of the difference in the vector magnitudes. Note that when ||u|| = ||v||, the term on the left reduces to w. As the magnitudes diverge, the term tends toward zero. The term multiplied to (1-w) is an exponential function with argument negative quantity 1 minus the dot product between u and v, divided by their magnitudes. When u and v have the same direction, <u,v>/||u|| ||v|| = 1, and the exponent as a whole is zero. When u and v are anti-parallel, <u,v>/||u|| ||v|| = -1 and the exponent is -2 so the term on (1-w) is exp(-2) which is approximately 0.135, which is close to zero. So when u = v, M(u,v) = 1 and when u and v are dissimilar in magnitude and/or direction, M(u,v) is closer to zero.

We now have a means of comparing the data from different pitchers to better populate our sample. To demonstrate this, we will again use C.J. Wilson’s data. First, we will run this method at a point near his sink: (-0.125,2.125). Since we will have up to eight vectors, we can fit an interpolating polynomial in between their heads to get an idea of what is happening for the full 360 degrees around the square. The choice of interpolating polynomial in this case will be a cubic spline function. This will give a smooth curve through the data without large oscillations. Working with only Wilson’s data, which is made up of 30 pitches, this looks like:

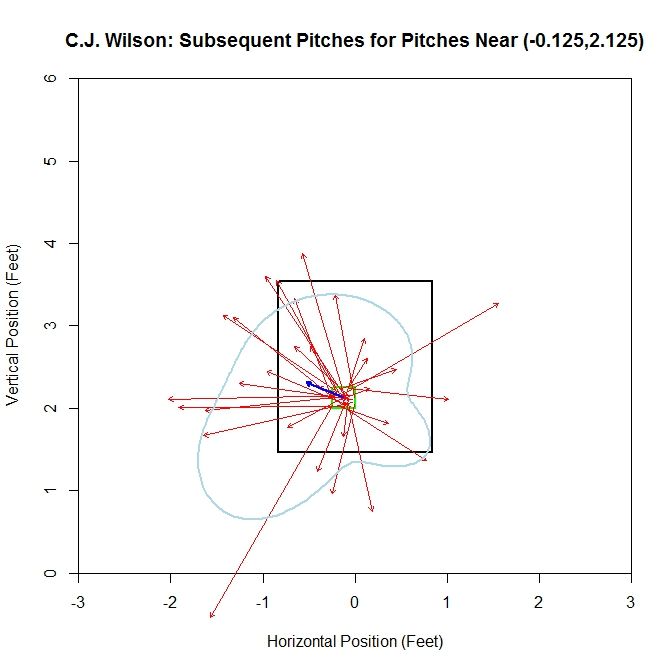
The vectors are spread out in terms of direction, but one vector which extends outside the lower-left quadrant of the plot leads to the cubic spline (light blue curve) bulging to the lower left of the strike zone. Otherwise, the cubic spline has some ebb and flow, but is of similar average distance all around.

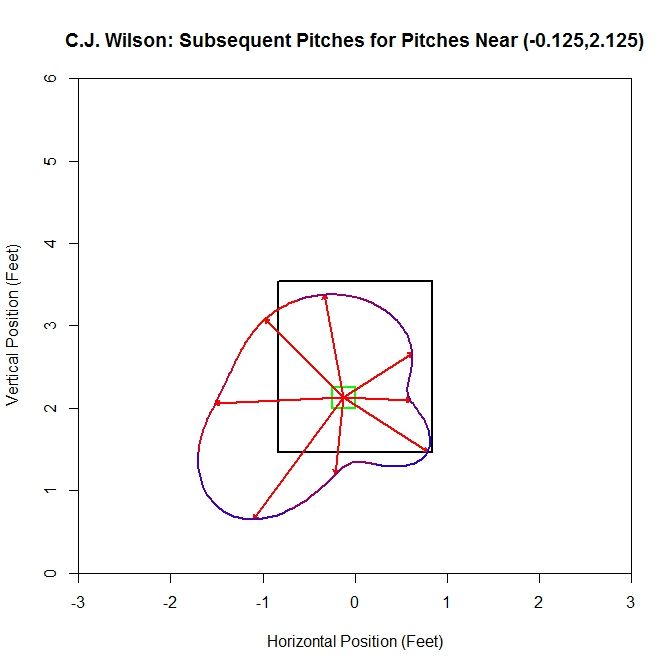
When we remove the vectors and replace them with the average vector of each octant (red vectors), we have a better idea of where the next pitch might be headed. We also color-code the spline to keep the data about the frequency of the pitches in each octant. Red indicates areas where the most pitches were subsequently thrown and blue the least. We see that the vectors are longer to the left and, based on the heat map on the spline, more frequent. However, a few short or long vectors in areas that are otherwise data-deficient will greatly impact the results. Therefore, we will add to our sample by finding pitchers with similar data in the square. We will compute the value of M between Wilson at that square and the top 200 pitchers in terms of most pitches thrown for the same season.

For Wilson, the top five comparable pitchers in the square (-0.125,2.125), with the value of M in parentheses, are Liam Hendriks (0.995), Chris Young (0.986), A.J. Griffin (0.947), Kyle Kendrick (0.943), and Jonathan Sanchez (0.923). Recall that this considers both average vector length and direction. Adding this data to the sample increases its size to 94 pitches.

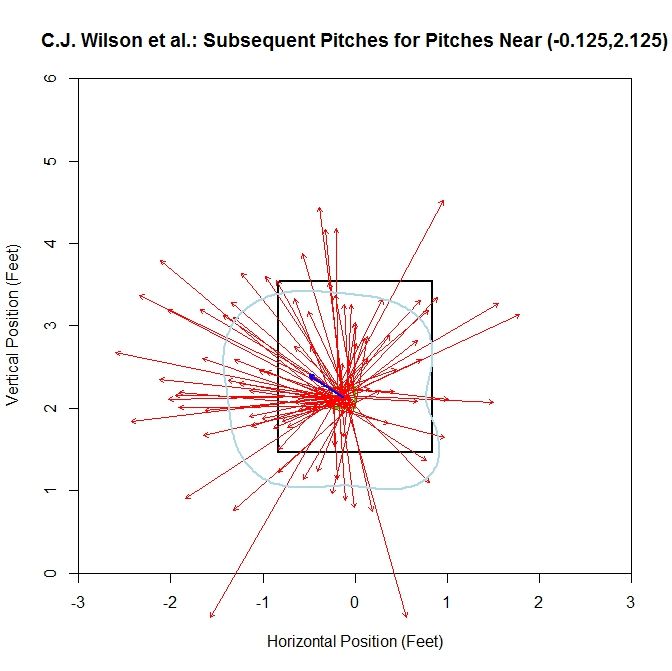
For this plot, the average vector (the blue vector in the center of the cell) is similar to that of Wilson’s solo data. However, since the number of pitches has essentially tripled, the plot has become hard to read. To get a better idea of what is going on, we can switch to the average vector per octant plot:

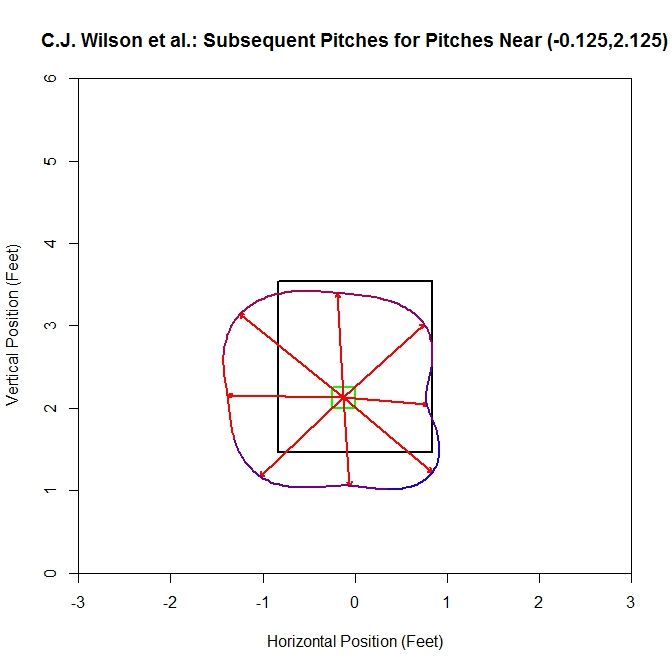
Examining this plot, most of the average vectors are in the range of 1-1.5 feet. The shape of the interpolation is square-like and seems to align near the edge of the strike zone, extending outside the zone, down and to the left.

We can also run this at points nearer to the edge of the strike zone. On the left side of the strike zone, we can work off of the square centered at (-0.875,2.375) (note that we drop the plots of the original data in lieu of the plots for the octants).

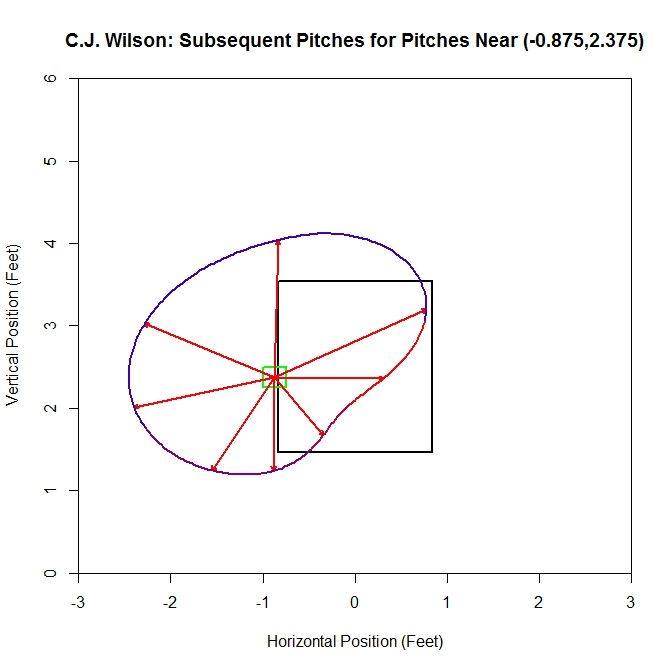
For the original sample, the dominant direction (where most of the vectors are pointed, indicated by the red part of the spline) is to the right, with an average distance of one to two feet in all directions. Now we will add in data based on the average vectors, increasing our sample from 15 to 97 pitches.

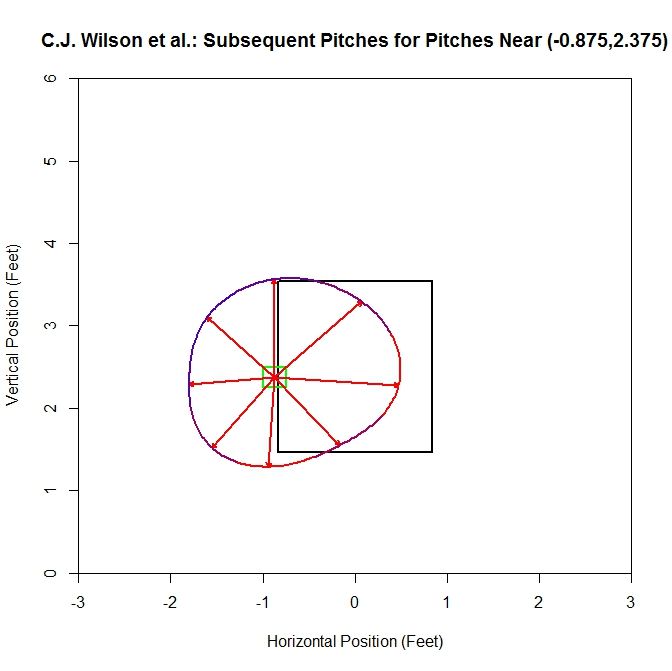
For the larger sample, the spline, which is almost circular, has average vectors approximately 1 to 1.5 feet in length. The preferred directions are to the right (into the strike zone) and downward (below the left edge of the strike zone). Also note that comparing the two plots, the vectors in the areas where there are the most pitches in the original sample (between three and six o’clock) have average vectors that retain a similar length and direction.

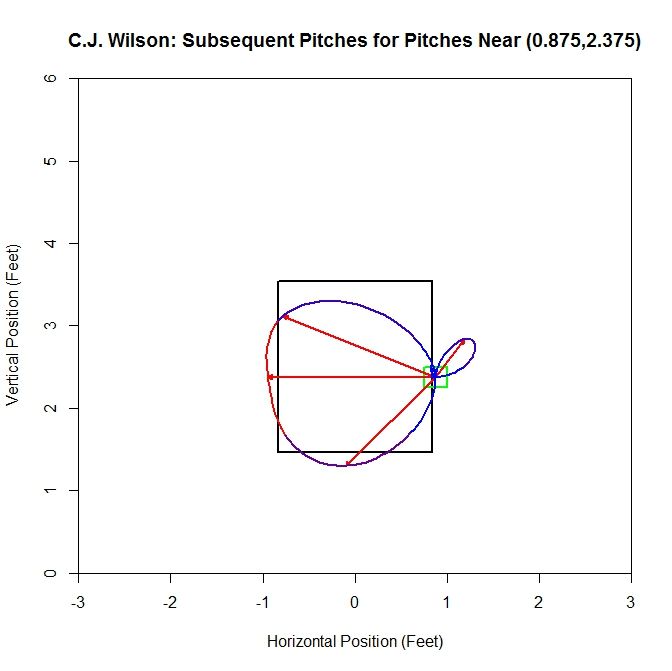
Switching sides of the strike zone, we can examine the data related the square centered at (0.875,2.375). For the original sample, the dominant direction is to the left with little to no data oriented to the right. Since there are octants that contain no data, we get a pinched area of the cubic spline. This is due to the choice of how to handle the empty octants. We choose to set the average distance to zero and the direction to the mean direction of the octant. This choice leads to pinching of the curve or cusps in these areas. Another choice would be to remove this octant from the sample and do the interpolation with the remaining nonempty octants.

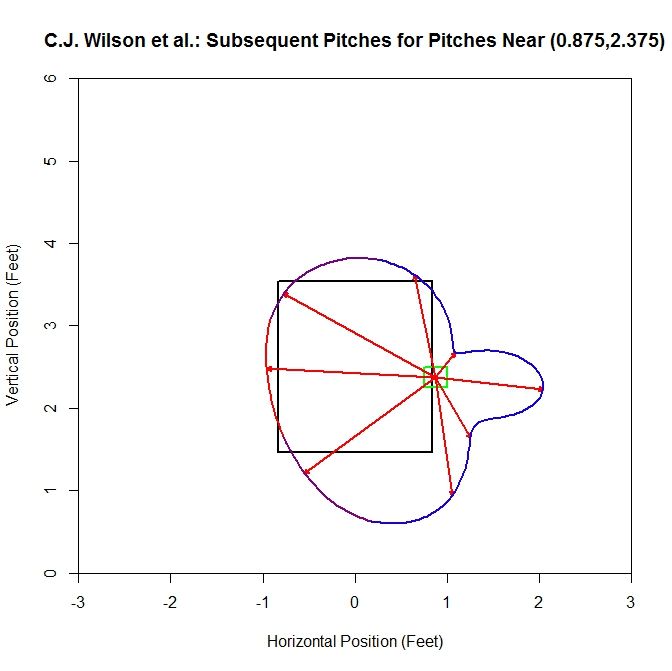
Adding data to this sample increases it from 9 pitches to 67, and the average vector and spline jut out on the right side due to a handful of pitches oriented further in this direction (this is evident from the blue color of the spline). In the areas where most of the subsequent pitches are located, the spline sits near the left edge of the strike zone. Again, the average vectors in the red area of the spline maintain a similar length and direction.

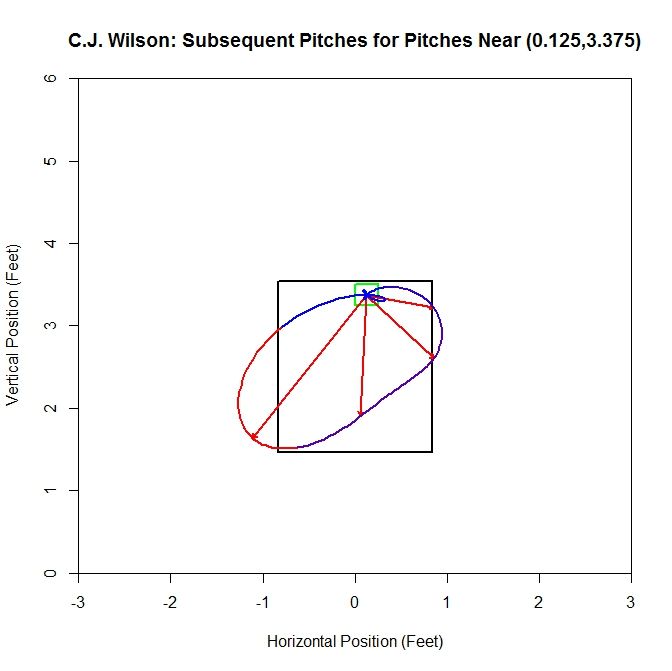
Moving to the top of the strike zone, we choose the square centered at (0.125,3.375). The original plot for a square along the top contains 11 pitches and no second pitches are oriented upward. There are only have four non-zero vectors for the spline and the dominant direction is down and to the left.

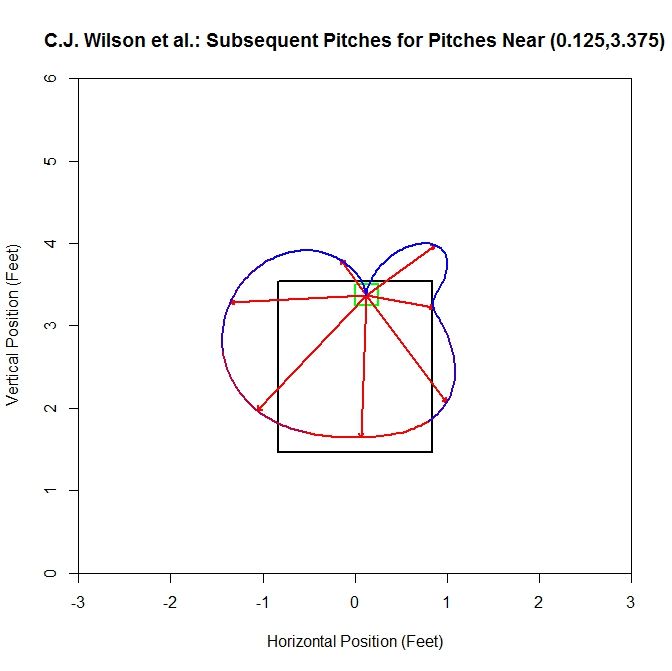
In this square, the sample changes from 11 to 72 pitches by adding similar data. Note the cusp that occurs at the top since we are missing an average vector there. Unsurprisingly, at the top of the strike zone, the preferred direction for the subsequent pitch is downward, and as we rotate away from this direction, the number of pitches in each octant drops.

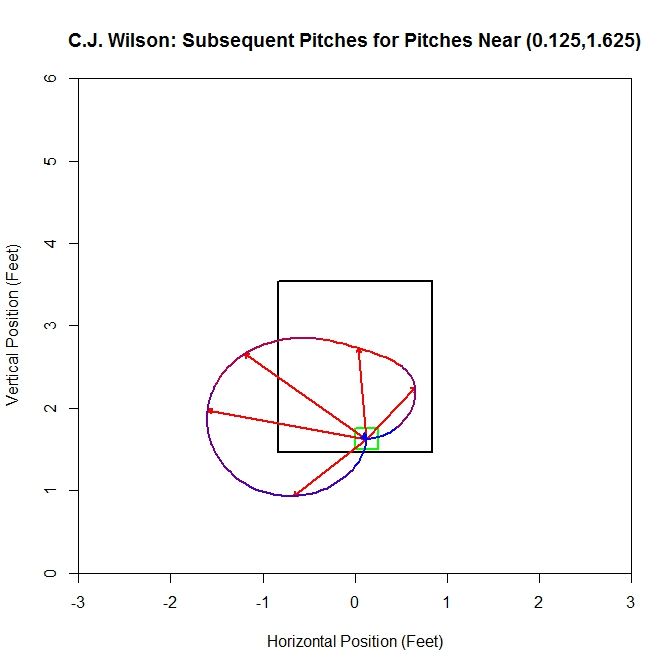
Finally, along the bottom of the strike zone, we choose (0.125,1.625). Starting with 27 pitches produces five average vectors, with the dominant direction being up and to the left.

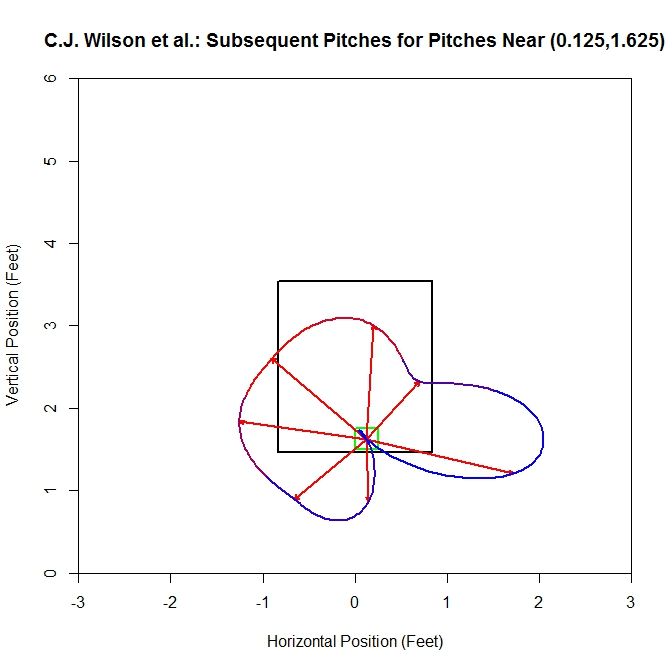
With the additional data from other pitchers, the number of pitches moves up to 87. The direction with the most subsequent pitches is up and to the left. In areas where we have the most data in the original sample (the red spline areas), the average vectors and splines are most alike.

There are several obvious drawbacks to this method. For the model fitting, we have some points in the strike zone with 30+ pitches and as we move away from the strike zone, we have less and less data for computing the averages. However, as we move away, the general behavior becomes more predictable: the next pitch will likely be closer to the strike zone. So the small sample should have less of a negative effect for points far away. This is also a potential problem since we use these, in some cases, small samples to calculate the average vector in each square, which is used as a reference point for adding data to the sample. It may be better to use the vector from the gradient field for comparison since it relies on all of the available data to compute the average vector (provided the gradient field approach is a decent model).

Another problem is that in computing the average vector, we are not taking into account the distribution of the vectors. The same average vector can be formed from many different combination of vectors. However, based on the limited data presented above, adding to the sample, using M and the average vectors, does not seem to have a large effect on octants where there is the most data in the original sample. These regions, even with more data, tend to retain their shape. These are also the areas that are going to contribute most to the average vector that is used for comparison, so this seems like a reasonable result.

A smaller problem that shows up near the edge of the zone is that we still occasionally, even after adding more data, get directions with only one or two pieces of data and this causes some of the aberrant behavior seen in some of the plots, characterized by bulges in blue areas of the spline. One solution to this would be to only compute the average vector in that octant if there were more than some fixed number of pitches in that direction. Otherwise, we could set the average vector to zero and the direction to the mean direction in that octant.

Obviously, an analysis of one pitcher over a small collection of squares in the grid does not a theory make. It is possible to examine more pitchers, but because the analysis must be done visually, it will be slow and imprecise. Based on these limited results, there may be potential if the process can be condensed. The pitching sink approach gives an idea of where the next pitch may be headed. As we move toward the sink, we have less information on where the next pitch is headed since near this point, the directions will be somewhat evenly distributed. As we move toward the edge of the strike zone, we get a clearer picture of where the next pitch is headed if only for the reason that it seems unlikely that the next pitch will be even further away.

While this model seems reasonable in this case, there may be cases where a more general model is needed to fit with the behavior of the data. To recover more accurate information on the location of the next pitch, we can switch to the octant method. Since some areas with this method will have very small samples, we can pad out the data via comparison of the average vectors. This seems to do well at filling out the depleted octants and retains many of the features of the average vectors in the most populated octants of the original samples. At this point, both these models exist as novelties, but hopefully with a little more work and analysis, they can be improved and simplified.

wRC is a very useful statistic.  On the team level, it can be used to predict runs scored fairly accurately (r^2 of over .9).  It can also be used to measure how much a specific player has contributed to his team’s offensive production by measuring how many runs he has provided on offense.  But it is rarely used for pitchers.

Pitching statistics are not so much based on linear weights and wOBA as they are on defense-independent stats.  I think defense-independent stats are fine things to look at when evaluating players, and they can provide lots of information about how a pitcher really performed.  But while pitcher WAR is based off of FIP (at least on FanGraphs), RA9-WAR is also sometimes looked at.  Now, if the whole point of using linear weights for batters is to eliminate context and the production of teammates, then why not do the same for pitchers?  True, pitchers, especially starters, usually get themselves into bad situations, unlike hitters, who can’t control how many outs there are or who’s on base when they come up.  But oftentimes pitchers aren’t better in certain situations, as evidence by the inconsistency of stats such as LOB%.  So why not eliminate context from pitcher evaluations and look at how many runs they should have given up based on the hits, walks, and hit batters they allowed?

To do this, I needed to go over to Baseball-Reference, as FanGraphs doesn’t have easy-to-manipulate wOBA figures for pitchers.  Baseball-Reference doesn’t have any sort of wOBA stats, but what they do have is the raw numbers needed to calculate wOBA.  So I put them into Excel, and, with 50 IP as my minimum threshold, I calculated the wOBA allowed – and then converted that into wRC – for the 330 pitchers this year with at least 50 innings.

Next, I calculated wRC/9 the same way you would calculate ERA (or RA/9).  This would scale it very closely to ERA and RA/9, and give us a good sense for what each number actually means.  (The average wRC/9 with the pitchers I used was 3.95; the average RA/9 for the pitchers I used was 3.96).  What I found was that the extremes on both sides were way more extreme (you’ll see what I mean soon), but overall it correlated to RA/9 fairly closely (the r^2 was .803).

Now, for the actual numbers:

The first thing that jumps out right away is that Koji Uehara had a wRC/9 of 0.08.  In other words, if that was his ERA, he would give up one earned run in about 12 complete game starts if he were a starter, which is ridiculous.  The second thing that jumps out is that most of the top performers are relievers – in fact, 12 out of the top 13 had fewer than 80 innings, with the only exception being Clayton Kershaw.  Also, the worst pitchers by wRC/9 had a wRC/9 much higher than their ERA or RA/9.  Pedro Hernandez, for example, had a wRC/9 of 7.68, and there were 6 pitchers over 7.00.  Kershaw actually has a wRC/9 that is lower than his insane RA/9, so maybe he’s even better than his fielding-dependent stats give him credit for.

But wait!  There’s more!  The reason we have xFIP is because HR/FB rates are very unstable.  So let’s incorporate that into our wRC/9 formula and see what happens (we’ll call this one xwRC/9):

Not a huge difference, although we do see Uehara’s number go down, which is incredible, and Tanner Roark’s – the second-best pitcher by wRC/9 – nearly double.  Also, Tyler Cloyd becomes much worse, and is now the worst pitcher by almost half a run per nine innings.  Kershaw’s wRC/9 goes up by a considerable amount, so much so that his xwRC/9 is now higher than his RA/9.  All in all, however, xwRC/9 actually has a smaller correlation with RA/9 (an r^2 of .638) than wRC/9 does, so it isn’t as useful. 

Now, logically, the people who outperformed their wRC/9 the most would have high strand (LOB) rates, and vice-versa.  So let’s look at the ten players who both outperformed and underperformed their wRC/9 the most.  The ones who underperformed:

We can see that everyone here – except for Koji Uehara, who had the fourth-highest LOB% out of all pitchers with 50 innings – is below the league average of 73.5%.  Only Uehara and Joel Peralta are above 70%.  Clearly, a low LOB% makes you allow many more runs than you should.  But what about Koji Uehara?  How did he allow all those runs (10, yeah, not a lot, but his wRC/9 was way lower than his RA/9) without allowing many baserunners to score and not allowing many damaging hits?  If you know, let me know in the comments, because I have no idea.

Now for the people who outperformed their wRC/9:

Just what you would expect:  high LOB%’s from all of them (each is above the league average).  Stephen Fife and Alex Sanabia are the only ones below 80%.

So what does this tell us?  I think it’s a better way to evaluate pitchers than runs or earned runs allowed since it eliminates context:  a pitcher who lets up a home run, then a single, then three outs is not necessarily better than one who lets up a single, home run, then three outs, but the statistics will tell you he is.  It might not be as good as an evaluator as FIP, xFIP, or SIERA, but for a fielding-dependent statistic, it might be as good as you can find.

Note:  I don’t know why the pitchers with asterisks next to there name have them; I copied and pasted the stats from Baseball-Reference and didn’t bother going through and removing the asterisks.

In fantasy, the 5 categories are meant to evaluate the overall value of a pitcher, and players that are best able to predict future value can win serious jelly beans. A pitcher accumulates Ks by defeating individual batters, while a low WHIP indicates that he can avoid putting opposing players on base. ERA evaluates a pitcher’s run prevention skill. Saves and wins are meant to measure a pitcher’s ability to dominate opposing teams, whether for an inning or an entire game. However, wins compare poorly with quality starts and W+QS when correlated with commonly used pitching statistics.

The chart below shows the correlation between wins, quality starts, and the combination of the two with other commonly used pitcher evaluation metrics. By calculating the correlation between these 3 categories and other pitcher metrics such as FIP, OPS allowed, batting average against, homeruns allowed per 9 innings, and runs above average by the 24 base/out states (RE24), we can measure not only the relationship between the variables, but also how much they differ from each other.

None of these statistics correlate as well with wins as they do with quality starts and W+QS. In fact, the difference between QS and W+QS is negligible in every case. This result makes sense—since QS make up the majority of the W+QS total, the two are almost identical in the chart. The actual values of each correlation are less important that the overwhelming conclusion that wins do not have much to do with pitcher skill, while the difference between QS and W+QS is negligible.

 Why, then, might it be useful to use W+QS? These results show that it may not be very different from using quality starts, but is far more reliable way to judge a pitcher’s performance than wins alone. W+QS double count the games when a pitcher goes somewhat deep into a game, pitches fairly well (3 ER or less), and exits the game while leading his opponent. This scenario might not be much different than the QS by itself, but it does retain an element of “winning the ballgame for your team”, which is what the win category somewhat accurately captures. A winning pitcher is generally on a winning team, although that statement may not mean much.

W+QS may be an unnecessarily complicated way to repeat the same evaluation standards as quality starts, but some players may prefer it simply because it retains the W while relegating it to a position of less importance. Maybe owning a great pitcher like James Shields doesn’t have to be so frustrating after all.

Even as a fan of a different AL East team, seeing Manny Machado go down with a knee injury this Monday saddened me. Fortunately, reports indicate the injury is not as serious as originally feared, and Machado could return for spring training. Machado is part of a class of young stars that have simultaneously taken baseball by storm and wrecked the grading curve for everyone to come after them. People are already giving up on Jurickson Profar because he isn’t a star at an age when most players are in Low-A ball. Bryce Harper ranks in the top 20 in the MLB in wRC+ at the age of 20, and hardly anybody notices.  Anyways, I digress. So where does Machado’s age-20 season rank?

Machado compiled 6.2 WAR in 2013, good for 10th in the MLB. In the last 55 years, only Alex Rodriguez in 1996 and Mike Trout in 2012 have posted a higher WAR in their age-20 season. Of course, there were some better seasons before then, but Machado probably wouldn’t have been allowed to play in those days.

Unlike Rodriguez and Trout, Machado’s offensive numbers, while impressive for a 20 year-old are league average overall. A-rod had a 159 wRC+ in ’96, and Trout had a 166 wRC+ last year. Machado managed a 101 wRC+, providing most of his value with the glove. UZR credited him with 31 runs saved, best in the majors. After a very hot start that was fueled by an inflated BABIP, Machado slowed down.

So what can Orioles fans expect from Machado going forward?

Machado is an aggressive contact hitter. His walk rate of 4.1% is one of the lowest in the MLB, and his strikeout rate of 15.9% is well below the MLB average. While Machado will never be Joey Votto, the walk rate will improve as he matures. His minor league walk rate was above 10%. Additionally, Machado should hit for more power. I could just say that he hit 51 doubles and those will turn into home runs. But, that would be lazy, and doubles don’t always turn into home runs as a player develops. Sometimes they turn into singles. Just ask Nick Markakis.

However, there are other reasons to believe Machado will hit for power. First of all, he has excellent bat speed, and there’s no lack of raw power. Some of the home runs he has hit are very impressive. Of the 14, ESPN Home Run Tracker classifies 10 of them as either No Doubters or Plenty.  The average speed off the bat was just a shade behind Robinson Cano. Furthermore, despite playing in one of the best home run ballparks in the league, and having an average fly ball distance on par with Nick Swisher, Machado’s HR/FB ratio of 7.9% is in the bottom third of the MLB. Bet on this ratio improving. While he does have a very high rate of infield flies (9th in MLB), he should be able to bring that down with improved discipline.

Hopefully for Orioles fans and baseball fans, Machado will have a complete recovery from his knee injury. It might be hard to live up to expectations after producing a 6.2 WAR season at age 20, but with improved offense Machado could be up to the task. Expect the plate discipline and power to improve, as the defense inevitably regresses from a season that stretched the upper bounds of UZR. It’s a very small group he’s in, but star players at age 20 tend to be stars at 25.

Throughout the pre-sabermetric revolution days of baseball, the statistics that determine fielding ability (namely errors and fielding percentage) had generated much criticism of fielding stats and undeserving gold glove award winners (Derek Jeter et al), and had kept fielding ability a mystery. However, this mystery in part led to the sabermetric revolution in baseball statistics. In the current day and age, with improved measures of performance available publicly, measuring fielding ability is somewhat less of an enigma, but still far from perfect.

One of the most often used fielding metrics in this day and age is UZR or Ultimate Zone Rating (click the link for an excellent FanGraphs explanation). Instead of counting perceived plays and errors, UZR records every batted ball hit to each of the numerous zones on the baseball field at each trajectory and the runs lost/saved as the fielder gets to the ball or falls short. This is found by matching the average result of the play with the Run Expectancy Matrix. Therefore, UZR provides a very accurate measure of how valuable that fielder was in terms of runs saved/lost over the course of the season.

However, there are major problems with UZR. Sample size issues cause large fluctuations from month to month and even year to year. Moreover, it does not provide a stable basis of fielding ability. Even when all players’ impacts are averaged to a constant, UZR/150, averaged to runs saved/lost per 150 defensive games, the metric is very volatile.

The reasons behind this might actually be easier to identify and correct than you might think. Let’s face it: not all fielders get the same amount of balls hit to them in the same place at the same trajectory within the same number of outs or innings. Infielders with a good knuckleballer on the mound and a slap hitter at the plate are going to get more grounders to each zone than infielders whose teams have fly ball pitchers on the mound and face lots of power hitters at the plate.

However, while the actual amounts may fluctuate from pitcher to pitcher and hitter to hitter, many fielders get a decent sample size of each batted ball to each zone over the course of multiple seasons. Even with a staff of fly ball pitchers, infielders will still handle their fair share of ground balls to each zone over the course of a season. So if there was a way to average all the pitchers and hitters together and measure the value and frequency of making a play in each zone based on the entire AL, NL, or MLB* average batted ball chart, then we could create a similar metric that would be more predictive, rather than purely descriptive.

*The purpose of separating the leagues is the discrepancy of hitting ability with the DH in the AL and the increased frequency of bunts (from pitchers) in the NL.

If we take the average percentage of batted balls to each zone with each trajectory for the AL, NL, or MLB and multiply that by the average runs saved/lost for plays made or missed in that zone, we can find a universal batted ball sample from which to apply the fielders’ impact. While this would not be directly proportional to the runs saved/lost for the fielder during that season for that pitching staff and the batters faced, it would be a metric independent of the impact that the pitcher and hitter has on the fielders. It would measure pure fielding ability over multiple seasons in the form of runs saved, but unbiased by the specific ratio of batted balls per zone and trajectory hit to the fielder over the seasons.

Predictive UZR will have sample size issues but when taken over multiple seasons, a starting fielder should get his fair share of batted balls hit to each zone with each trajectory. The percentages for his success rates at each zone and trajectory can then be applied not to the actual ratio of batted balls per zone hit his way (from his team’s pitching staff and hitters faced) but rather the average ratio of batted balls per zone hit in the entire AL, NL, or MLB.

Both UZR and Predictive UZR are very valuable for different things. UZR is a good reflection of the fielder’s direct impact on defense for the season. However, this might not accurately reflect the fielder’s true talent level because of the assortment of batted balls hit his way. Predictive UZR, while not a concrete reflection of the past runs saved, is a more pure measure of fielding ability. It can provide a number that, when compared to UZR, tells which fielder got lucky and which fielder did not, based on his pitching staff and the hitters faced. Another interesting twist the concept of Predictive UZR brings is that it can be based on the average batted ball chart of teams, divisions, and differing pitching staffs in addition to the AL, NL, or MLB. So a fielder’s projected direct impact, or UZR, can be transferred more easily as he moves from team to team, forming the basis of more accurate fielding projections.

Predictive UZR is not by any means a substitute to UZR, but rather complements it and works with it in intriguing ways. It is a concept worth looking into that has the potential to leave fans, media and front office personnel better informed about the game of baseball.

Nik Oza
Georgetown Class of 2016
Follow GSABR on twitter: @GtownSports

This is part two of a three-part series detailing a method of judging pitch framing based on the prior probability of the pitch being called a strike.  In part 1, we motivated the method.  Here in part 2, we will formalize it.

The formula we’ll use for judging catcher framing is pretty simple on its face. For each pitch delivered, we calculate a value

IsCalledStrike + prob(CalledStrike)

Here, IsCalledStrike is simply 1 if the pitch is called a strike, and 0 otherwise.  The second term is the probability that the pitch would have been called a strike, absent any information about the catcher’s involvement. We add up these values for every called ball or strike that a catcher receives, and report the resulting number.  Since this method is essentially identical to defensive plus/minus, I’ve taken to calling it Catcher Plus/Minus (CPM), although someone reading this can probably come up with something better.  I should mention the following: it has been brought to my attention that this method has been developed before.  However, I can’t find it written up anywhere on the web.  So you are welcome to consider this the documentation of an existing method, if you’d like.

Read the rest of this entry »

Note: I have no idea if I’m the first to do this, but quite frankly I don’t care.

It’s no secret that Yankees second baseman Robinson Cano is an all-around excellent player, as he’s on his way to his fourth consecutive 5-win season. It’s also no secret that he’ll be a free agent after this season, and will certainly receive a contract in the nonuple figures. As the Angels have shown these past two offseasons, when you spend that much money on one player, you’d better be sure he’ll be worth it; the Yankees already have experience with terrible contracts (contracts they’re still due to pay for), so they’ll have very little room for error. Thus, executives of any and every team that might be interested in Cano will be doing their research, scouring the earth for any warning signs of a possible decline.

But back to Cano’s performance at the moment. While Cano is a superb player overall, much of his value comes from his bat; over this current 4-year 5-WAR streak, he’s been the seventh-best offensive player in the majors. The (relative) caveat in his game, therefore, is his defense: over that same span, he’s just 76th in fielding in the majors. Defensive statistics are subject to year-to-year fluctuations, and the fluctuations of Cano’s defense have been well documented. However, there’s a specific aspect of his defense that I’d like to focus on for the time being.

As you probably should know, UZR–the main defensive statistic at FanGraphs–is composed of four parts: RngR, which measures how many runs a player saves or costs his team with his range; ErrR, which measures how many runs a player saves or costs his team by committing or not committing errors;  ARM, which measures how many runs a player saves or costs his team with his arm in the outfield; and DPR, which measures how many runs a player saves or costs his team by turning or not turning double plays. This last segment is the one that is so interesting, at least to me, because it’s the one that Cano is the worst in the league at.

No, really. Among 79 qualified infielders¹, Cano’s DPR of -3.6 is the worst, and the next worse player (Neil Walker) is a full 1.2 runs away, at -2.4 DPR².

Now, the real question becomes: what (if anything) does this mean? Obviously, when you’re preparing to give someone a contract that could exceed the GDP of whatever the fuck this country is, you’d prefer if he wasn’t the absolute worst in the majors at something, even a seemingly trivial thing like turning double plays. Still, though, it’s worth asking: what, exactly, is the significance of this?

There are a few different ways of looking at this; for the purpose of this post, I divided my analysis into 5 main categories:

1. Is this a fluke?

As I mentioned before, year-to-year defensive statistics can be quite fickle, so it’s best to gain some historical perspective when evaluating a player’s defense³. So, does Robinson Cano have a history of being a bad double play turner?

Well, on the one hand: In 2011, he was 6th out of 73 qualified infielders in DPR; in 2010, he was 13th out of 81; and in 2007, he was 2nd out of 89. These numbers would suggest that his horrific 2013 has been a fluke, except…

Last year, he was 61st out of 76; in 2009, he was 77th out of 81; in 2008, he was 67th out of 78; in 2006, he was 62nd out of 89; and in 2005, he was 75th out of 77.

Add it all up, and since he entered the league in 2005, Cano is 83rd out of 95 qualified infielders in DPR. However, it should be noted that before this year (i.e. from 2005 to 2012), Cano was 55th, a much more respectable figure, if not a particularly great one.

So, overall, it’s fairly safe to conclude that Cano has something of a poor history of turning double plays. What next?

2. Does a poor DPR correlate to poor defense in other areas?

To answer this question, I’ll bring up a few graphs. These’ll show us how well DPR this year has correlated to RngR…

…ErrR…

…UZR…

…and finally, whatever that Def stat is.

In case you were wondering, the R-squared values for these graphs were .000669, .004252, .028772, and .032933, respectively.

So there’s clearly no correlation between DPR and any other defensive statistic, which brings up the original question: What’s the point of all of this? Well…

3. Just how bad is a -3.6 DPR?

Quite bad, it turns out. In the illustrious 12-year history of the stat, the only worse seasons were Jas0n Bartlett in 2009 (-4.2)⁴, Yunel Escobar in 2008 (-3.7), and Omar Vizquel in 2005 (-4.0).

Again, this takes me back to my original point: when a player’s going to be paid a yearly salary that will exceed the total gross for this shitty movie, you generally don’t want him mentioned among the worst players in history (albeit a very short history).

Still, though, these three were/are good defensive–and all-around–players for the majority of their careers. So what’s to worry about?

4. How have players with similarly poor DPRs done in their seasons?

For this one, I’ll expand the criteria to all seasons with -3 DPR or worse; other than Cano this year, there are 11 such seasons:

Of these 11 seasons, the average WAR was 2.8, less than half of Cano’s WAR this year. The highest WAR was Bartlett’s 5.3 in 2009⁵, but overall the results were much lower.

So it would appear that Cano’s done something relatively new this season–play at a very high level while having a substandard DPR–but this still doesn’t answer the main question. I’ll answer that next, and the results are intriguing:

5. How have other players with DPRs this bad done for the rest of their careers?

Let’s continue to look at these 11 seasons. How were these players before and after their -3 DPR season?

(All values are per 600 PAs. Year of DPR is included in Pre.)

They all saw a noticeable drop off in their WAR; the only ones whose WAR increased were Rollins and Walker, and they had their bad seasons when they were young. Given that Cano will turn 31 in October, it’s safe to say this will not happen to him. Since Cano is getting older, a decrease in WAR to some degree should be expected, especially considering the volatility of his position; this has been covered before, though.

What I found interesting, though, was that the players’ defense (as measured by that fancy new Def stat) didn’t really drop off much after the bad DPR year, but their offense seemingly fell off a cliff. This goes against the theory of player aging curves (that offense can get better as players get older, but defense tends to just decline overall).

Obviously, this is a very small sample size, and to extrapolate anything meaningful from it would be foolish. Also, it’s pretty unlikely that the decline was caused by one bad year turning double plays.

This post as a whole was probably rather cockamamie⁶, but then again, everything I post here tends to be. I just hope I was able to raise some interesting questions about how much turning two matters to a player’s overall worth. Perhaps, years from now, when the Yankees are paying Cano $30 million a year to hit .250 with poor defense, and the Orioles have won the division year in and year out, I’ll be able to look back with pride at my prescience.

Or maybe, the Yankees will just win more World Series with or without Cano, while the Orioles dwell in mediocrity every year.

A man can dream, though….

——————————————————————————————————————

¹For some reason which escapes me, there isn’t an option to sort the leaderboards by solely infielders, even though there’s an outfielder option.

²Hopefully, you would’ve figured that out on your own, but I put it in there just to be safe. Also: All stats are as of Saturday, September 21st, 2013.

³Otherwise, you’ll end up with pieces-of-shit “analysis” like this.

⁴Bartlett also had a DPR of -3.8 in 2006, but he didn’t qualify that season.

⁵That was his ridiculous fluke season–you know, the one that Joe Maddon just gets out of every scrub the Rays find on the street.

⁶You have no idea how long I’ve waited to use that word.

I’m generally opposed to the sacrifice bunt, except in the rarest of circumstances. This less than optimal strategy is utilized even more in the playoffs. Derek Jeter, the all-time leader in playoff sacrifice bunts with 9, bunts almost twice as frequently in the playoffs as the regular season. That in itself should tell you that managers tend to go bunt-happy in the postseason since Jeter is a career .308/.374/.465 playoff hitter. I used Win Probability Added (WPA) and Run Expectancy (RE) in my calculations. For the record, the sum of Jeter’s sacrifices is -0.13 WPA and -1.88 RE. Anyways, here’s the list of the five worst playoff sacrifice bunts since 2002. Data is provided by Baseball Reference’s Play Index.

5. Daniel Descalso 2012, NLDS, Game 1. The Cardinals were losing to the Nationals 3-2 in the 8th when Descalso came to the plate with Adron Chambers on first and Tyler Clippard on the mound. Descalso laid down a bunt, sending Chambers to second. WPA: -0.04 RE: -0.19. Pete Kozma and Matt Carpenter would be retired, and the Nationals would go on to take Game 1. Descalso would hit two home runs in the series.

4. Eric Bruntlett 2004, NLCS, Game 6. Down 4-3 in the 9th, the Astros pinch-hitter faced Cardinals closer Jason Isringhausen with Morgan Ensberg on first and no outs. Bruntlett had 4 home runs and a 111 wRC+ in 61 regular-season PA, but a go-ahead home run was not on manager Phil Garner’s mind. Bruntlett bunted Ensberg to second. WPA: -0.05 RE: -0.21. After Craig Biggio flew out, Jeff Bagwell would deliver a game-tying single, but the Cardinals would eventually win it in the 12th. Though I’m not a fan of judging decisions based on results rather than process, you could say that this decision “worked.”

3. Brad Ausmus 2005, WS, Game 4. The Astros were trailing 1-0 when Jason Lane led off the bottom of the 9th with a single off White Sox closer Bobby Jenks. The 36 year-old catcher had posted a .351 OBP in 2005, one of the best marks of his career. Nevertheless, he sacrificed on the first pitch he saw, moving Lane to second and decreasing the Astros’ chance of scoring. WPA: -0.05 RE: -0.21. Pinch hitters Chris Burke and Orlando Palmeiro would be retired, and the White Sox took game 4 on their way to winning the series.

2. Elvis Andrus, 2010 ALCS, Game 1. The Rangers shortstop came to the plate against Mariano Rivera in the bottom of the 9th inning, with the Rangers trailing 6-5 and Mitch Moreland on first with no outs. With the count at 1-2, Andrus got down a bunt, sending Moreland to second. WPA: -0.06 RE: -0.22. Rivera would strike out Michael Young and get Josh Hamilton to ground out, ending the game. This bunt is even worse than the numbers because of the 1-2 count on Andrus and the fact that there was little to no risk of grounding into a double play, as the speedy Andrus had just 6 GDP in almost 700 PA. I should add that noted lover of bunting Ron Washington was managing the Rangers, who have had the most sacrifice bunts in the AL during his tenure.

1. Danny Espinosa, 2012 NLDS, Game 1. The Nationals were trailing the Cardinals 2-1 in the top of the 8th. With Ian Desmond on first and Michael Morse on third and no outs, Espinosa came to the plate, facing Cardinals reliever Mitchell Boggs. Espinosa was 0-3 on the day with 3 strikeouts. He still had some pop though, as he had 17 home runs on the season. For whatever reason, on an 0-1 count, Espinosa tapped a bunt to Boggs, advancing Desmond to second. WPA: -0.09 RE: -0.44. The next hitter, Kurt Suzuki, would strike out. Fortunately for Espinosa and the Nationals, pinch hitter Tyler Moore would come through with a two-run single, and the Nationals would win the game 3-2.

The sacrifice bunt by a position player is almost universally a negative play, but even in the age when statistical information is readily available and most teams are employing an army of nerds, the tactic refuses to die. Perhaps it’s because “that’s the way the game was played” when many of these managers were players. Or maybe it’s the conservative nature of managers. The players usually get saddled with the blame if an opportunity with runners in scoring position is squandered after a sacrifice bunt. But if a player grounds into a double play when he could have bunted, the manager might be taking the heat. Whatever the case, expect managers to keep ordering the bunt come October.