Perspective
How we rank players in our own minds can tell us a lot about what we value in a ballplayer. For decades the statistics that mattered to sportswriters and the public at large were those that were simple, easily understood, and still relevant to the game. Stats like batting average (AVG), runs batted in (RBI), and home runs (HR) were regularly quoted when writing articles or voting for MVP awards. Each of these numbers tells a piece of the story of what a ballplayer is. AVG shows a players ability to put a ball in play and reach base, RBI is a representation of run creation and hitting while men are on base in front of you, and HR show your power in hitting.

These numbers still hold great significance today. That said, they are not flawless expressions of player prowess with the bat. A player could have a high average and still struggle to get on base often due to strikeouts or weak contact. RBI is often a product of opportunity as much as hitting success. After all, you can still receive RBI when creating an out. HR meanwhile can be a very one-sided affair if your average is low, leading to an all-or-nothing scenario for a hitter.

I’m not trying to disparage anyone from using AVG, RBI, and HR in a debate of great players, but when you use them keep in mind that they make up only a fraction of what a ballplayer can be.

Modern statisticians have begun using much more advanced numbers like WAR or OPS+ to determine a players quality. These numbers take into account positional skill differences, park factors, and many other aspects of the game. Much like the traditional stats mentioned before, these stats have both positive and negative aspects to them. No one stat can give you a complete picture of a player’s skillset and value.

Whenever an article comes out discussing the quality of a player’s career or season we often get quotes like these:

“Since Trout debuted in 2011, he leads all players with 37.9 WAR. Further, that 37.9 WAR through Trout’s age-23 season are the most by a player in the modern era.” — ESPN Stats & Information

OR…

“Harper finally displayed his prodigious tools last season, as he led the National League in runs (118) and home runs (42) while leading MLB in OBP (.460) and slugging percentage (.649).” — ESPN Stats & Information

While all of the numbers in these quotes are valuable, and even more so impressive, they come with very little context with respect to the league as a whole. It’s great that Trout has 37.9 WAR since 2011, but who is second? And by how much is he second? So Harper led the league in OBP, but what was the league average? Or how many plate appearances did he have? Did he miss any time with injury?

Each of these questions would further add to our understanding of the value and quality of the players mentioned, but that information is never going to be answered in this context. Additionally, this practice of “cherry picking” the best stats to fit our argument negates the whole and presents the players out of context. For example, these numbers neglect the fact that Harper struck out about 25% of the time that season. Even by today’s standards that is a lot of strikeouts. I understand of course that a lawyer is never going to give out unnecessary information about a client’s failings, but in the context of ranking players it is paramount that we take into account as much of the information as we can. Ultimately, we find ourselves back where we started.

If all stats are flawed, then how are we to determine an adequate ranking for players? I propose that we use more stats. That’s right. More stats, not less.

When you fixate a ranking on a single stat, then that stat accounts for 100% of your result every time. It doesn’t matter if the stat is meant to incorporate a host of stats together. Your results are the result of a singular point of reference. If you use three stats, then each is equivalent to one-third of your conclusion.

What would happen if we used 20 different stats to determine a ranking? While each individual stat is devalued, the whole average together will give us a better understanding of the whole spectrum of a player’s ability in the game. Be warned…results may incite head-scratching.

There is a great axiom in the world of baseball stats that goes something like this: “Just because a stat has Babe Ruth at the top and Mario Mendoza at the bottom does not mean it is a good stat.” Like all statistical analysis, take this one with a grain of salt.

Methodology
My process here is rather simple. Take a group of player data, a single year or all-time, across 20 stats. Rank each player individually against the others in the set from 1 to the total number of players across all the data. Finally, average each player’s rankings across the 20 stats. Our result…rAVG (Rank Average).

For ease in data gathering and processing, I’ve decided to use the 19 dashboard stats from FanGraphs plus hits to make 20 total stats. For all-time stats, the pool of players has been limited to players with a minimum of 5,000 plate appearances.

Notes:
• Each position has t50/b50: how many times a player ranks in the
  top 50 or bottom 50 across all categories.
• * denotes active player.

All-Time • Position Players (895 total)

Name - Pos

rAVG

t50

b50

1

Willie Mays - OF

93.2

17

0

2

Barry Bonds - OF

95.3

16

0

3

Tris Speaker - OF

105.3

15

0

4

Rogers Hornsby - 2B

110.7

16

0

5

Stan Musial - 1B/OF

113.6

17

0

6

Ty Cobb - OF

118.2

16

0

7

Alex Rodriguez* - SS/3B

118.9

15

1

8

Honus Wagner - SS

133.1

14

0

9

Mel Ott - OF

136.2

15

0

10

Eddie Collins - 2B

136.6

16

0

11

Babe Ruth - OF

137.2

16

1

12

Hank Aaron - OF

143.6

14

0

13

Mickey Mantle - OF

147.7

15

1

14

Ted Williams - OF

150.2

16

2

15

Lou Gehrig - 1B

156.1

15

1

16

Charlie Gehringer - 2B

158.5

13

0

17

Larry Walker - OF

159.7

13

0

18

Chipper Jones - 3B

162.4

15

0

19

Frank Robinson - OF

163.2

14

1

20

Jimmie Foxx - 1B

167.8

16

1

102

Mike Piazza - C

272.7

9

2

Thoughts

1. Larry Walker. At first glance this list appears to contain all the requisite names for a best-of-all-time list… that is until you reach #17 Larry Walker. I can assure you that I have not fudged the data in anyway. I, like you, are equally as shocked to find Mr. Walker parading alongside greats like Ruth, Mays, and Gehrig. Maybe we all should re-evaluate our opinions on Larry Walker.
2. Mike Piazza. I have included him at the bottom of the chart, because he is the highest-ranking catcher of the 73 that met the 5,000 plate appearance requirement. While ranking #102 would appear to be a slight to him, when viewed in the context of the total list of 895 players…Piazza ranks in the top 12% of all players in history.
3. Babe Ruth. Many of you, me included, probably feel that there is no way that the Great Bambino could rank outside of the top 10 all-time. I will remind you that this list is a ranking of statistics. It cannot evaluate impact on the game, cultural relevance, or popularity. It simply counts each stat as 5% of the whole and spits out a result. A closer look at Babe’s numbers and you will find that he was a terrible baserunner (SB & BsR) and his defense left much to be desired as well. Out of 421 outfielders he ranks 229 in SB, 411 in BsR, and 110 in Def. All this serves to remind me that no player, however great they might be, is without deficiencies.

Conclusion
As part of my research into this topic I ran numbers for each of the nine positions all-time and the cumulative all-time list seen above. In order to keep this article from becoming a novel, I’ve chosen to only include the top 20 of all-time here. The rest of this information will be available for viewing some time in the near future either on here or on my website.

While I may not agree entirely with the outcomes of this exercise in rankings, I do feel that it has caused me to better consider the totality of a player’s stat line rather than a few simple metrics. No one stat can give you a well-rounded, complete view of a player’s value and skill.

I await your fevered comments below.

As I write this post the KC outfield defense is ranked No. 1 in Defensive Runs Saved (DRS) with 43, and is No. 2 in UZR at 28.6 (first is the Cubs with 29.0).  KC sports one of the best, if not the best defensive outfield in the majors this season.

Detroit on the other hand has a fairly poor one.  They rank last in DRS, with -44, and last in UZR at -31.8.  Though Baltimore gives them a good run for their money, Detroit is probably the worst defensive outfield in the majors so far this season.

So I wondered if we could do an analysis to show what would happen if we substituted them entirely for one another?  How would that work?  Well, one simple approach would be to just use the DRS metrics for each team and basically say that DET would go from -44 to +43, so that’s a swing of +77 runs. Using the 10 runs per win thumb-rule, that’d be a pretty big swing, nearly eight games. Detroit is a whole lot better.  But I’m not sure this method is really the best we can do.  After all, we have all this Statcast data now.  Could we use that?

I set out to try to do just that.  So my first step was to hypothesize that the likelihood of a ball hit to the outfield actually dropping for a base hit could be correlated to the launch angle provided by Statcast and then that this likelihood would change depending on the team.  So to test this theory out I went to Baseball Savant and grabbed all the Statcast data for balls hit to the outfield for KC and for Detroit.

The KC data consisted of 1722 balls hit to the OF (when removing the few points that had NULL data for launch angle).  I took these 1722 points and bucketed them by launch angle in buckets that were 2 degrees each.  I then calculated the percentage of hits to total (hits + outs) for each bucket.  This percentage was the likelihood that a ball hit to the outfield at a certain launch angle would end up being a base hit.  This led me to my first realization, which was that anything that was basically < 8 degrees on launch angle (so including all negative angles), and made it to the OF, was a guaranteed hit.

The results of this analysis for the 1722 KC points made a lot of sense intuitively.  As the launch angle increased, so did the likelihood that it was an out, so my hit percentage trend went down.  Using a simple linear regression projecting the likelihood of a hit by angle had a 92.5% R^2.  This equation was going to work nicely.

I’ve been a Washington Nationals fan since the team moved to D.C. in 2005. One of my favorite players to watch — though he was with the team for just two seasons — was Adam Dunn. The 6’6, 250-pound lefty masher was an incredible physical specimen who could hit home runs like nobody’s business. Unfortunately, the only thing he did better than hit homers was strike out. He’s 36th on the MLB all-time home run list with 462, and third on the all-time strikeout list with 2,379. Because of his high strikeout numbers and sub-par batting average on balls in play, he sported a lifetime batting average of just .237.

I bring up Adam Dunn because he’s a prime example of the baseball truism that I’ll be investigating today: Do power hitters tend to strike out more often?

This claim is deceptively tough to evaluate because there’s no one clear way to tell if, and to what degree, a player is a power hitter. I came up with as many rational ways to measure power as I could and compared each with strikeout rates. I’ll let you decide for yourself exactly how well each metric relates to power.

Traditional Stats

Let’s start with the most obvious measure of a power hitter: Home-run hitting.

Here’s the correlation between a player’s home-run rate (HR/AB) and strikeout rate (K/AB).

r = 0.527

A correlation coefficient of 0.527 isn’t bad, and you can see a clear upward trend in the data, but let’s keep going.

Home runs obviously aren’t the only way to measure power. Let’s see what happens when we expand our study from home runs to all extra-base hits.

r = 0.427

So it turns out there’s actually even less of a correlation with extra-base-hit rate than with home-run rate.

There is a flaw to evaluating power using per at-bat rates. If a player has a high strikeout rate his rate of any type of hit will be lower. Here’s what happens when we redo the previous two graphs using home runs and extra-base hits per hit instead of per at-bat.

r = 0.609

r = 0.627

Much higher correlation. Correlation in the .600 range isn’t the goal — but it’s definitely an indication that something’s there. Since non-per-at-bat rates seem promising, let’s try per ball in play as opposed to per hit.

r = 0.634

r = 0.669

Even stronger correlation. Let’s move on now to a classic measure of power: Isolated power (ISO).

r = 0.508

Good correlation, but not as strong as we just saw with HR and XBH per hit and per BIP. But when you look at what ISO actually is, it’s a per-at-bat rate statistic.

Why don’t we redo ISO as per hit or and per ball in play instead of per at-bat?

r = 0.642

r = 0.673

So it turns out reworking ISO as per ball in play actually gave us our strongest correlation yet at 0.673.

Side note: I tried adjusting the ISO coefficients a couple of different ways since valuing a triple twice as much as a double and a home run three times as much as a double but just 1.5 times as much a triple seemed odd to me. As it turned out, the correlation didn’t get any better. Touché sabermetrics community, touché.

Statcast Stats

One of the great things about doing this study in 2016 is that we aren’t limited to traditional outcome-based stats. That being said, one of the less great things about doing this study in 2016 is there’s only one full season of publicly available Statcast data. As a result, I’m lowering my minimum observations per player from 1000 plate appearances to 100 at-bats. For context Manny Machado led the league in plate appearances in 2015 with 713. So we’re clearly going to see decreased correlation because of poor sample size. To give you an idea of what that looks like, here’s a few of the correlations from the previous section compared with what they would have been had I used 2015 Statcast data instead:

What you should take from this is that the strength of pretty much all of the correlations we’re going to look at will be diluted. Many stats that appear to have rather weak correlation could have a real relationship given more data, we just can’t know. It’s unlikely we’ll see some really indicting evidence that a specific measure of power implies a higher strikeout rate, but it could give us a good clue of where to look in the future. So with that out of the way, let’s crunch some numbers.

One obvious way to use Statcast to measure power is to look at exit velocity. If you tend to hit the ball hard, chances are you’re a power hitter. Here’s how average exit velocity correlates with strikeout rate.

r = 0.338

There’s some correlation, albeit pretty weak. Perhaps power isn’t best represented by whose hits on average are the hardest but rather who has the highest rate of very hard-hit balls. Home runs tend to be hit at least 95 mph, so let’s check the correlation between rate of 95+ mph balls in play and strikeout rate.

r = 0.393

There’s better correlation, but it’s still rather weak. Let’s move on.

Next up is launch angle. Power hitters hit more fly balls because that’s the only way to get a ball out of the park and a common way to hit a double.

r = 0.260

There’s even less correlation than with exit velocity, and when I looked at the rate of “home-run launch angles” (25˚ – 30˚) the correlation went down even further to 0.093. While we’re on the subject, I checked the correlation for the rate of balls in play that both had an exit velocity of at least 95 mph and a launch angle between 25˚ and 30˚ and got 0.323 — lower than both exit velocity-only correlations.

Perhaps distance will yield better results. Below is the correlation between average ball in play distance and strikeout rate.

r = 0.353

Still not much correlation, but as with exit velocity it would make sense for the true sign of power to be high rates of balls in the 300 feet range rather than the exact distribution of balls hit 100/200 feet.

r = 0.398

So we see improved correlation, but 300 feet was a rather arbitrary number. Let’s try 350 feet.

r = 0.481

There’s some decent correlation here, but maybe we’ve made a mistake in lumping together distances to all parts of the field. Here’s what happens when we redo the previous two graphs but only count balls hit to center field that went an extra 50 feet.

r = 0.416

r = 0.463

The correlation went up from 300 to 300/350 and down from 350 to 350/400 (interestingly both by .018). This brings up an interesting question: Does power manifest itself more or less on balls in play in different parts of the field? In looking at this I organized players by their handedness — dividing balls in play by pull/center/opposite field not LF/CF/RF. (I omitted switch-hitters from this part and looked only at balls hit to the outfield.) Rather than show 21 graphs, I made a table below with the correlation coefficients.

The last stat I’m going to look at is arc angle. Arc angle is a stat I created to evaluate a batted ball’s trajectory. You can find out more about it in my Hardball Times article. Just note that it’s only for balls hit in the air and lower angles are fly balls while higher angles are line drives.

r = -0.474

So none of the Statcast stats yielded a correlation coefficient of 0.5 or more. As I said at the top this is likely — at least in part — a sample-size issue. I’ll update these numbers after the season to see what difference that makes.

Recap

That was a lot, so here’s a table of all the correlation coefficients and increase in strikeout rate per unit of the stat for the comparisons we made.

As to our initial question: Does power correlate with strikeouts? I think it’s pretty clear that yes, power correlates with strikeouts in some capacity. As for how much it correlates and what exactly power is? That’s not clear. Hopefully additional seasons of Statcast data will help.

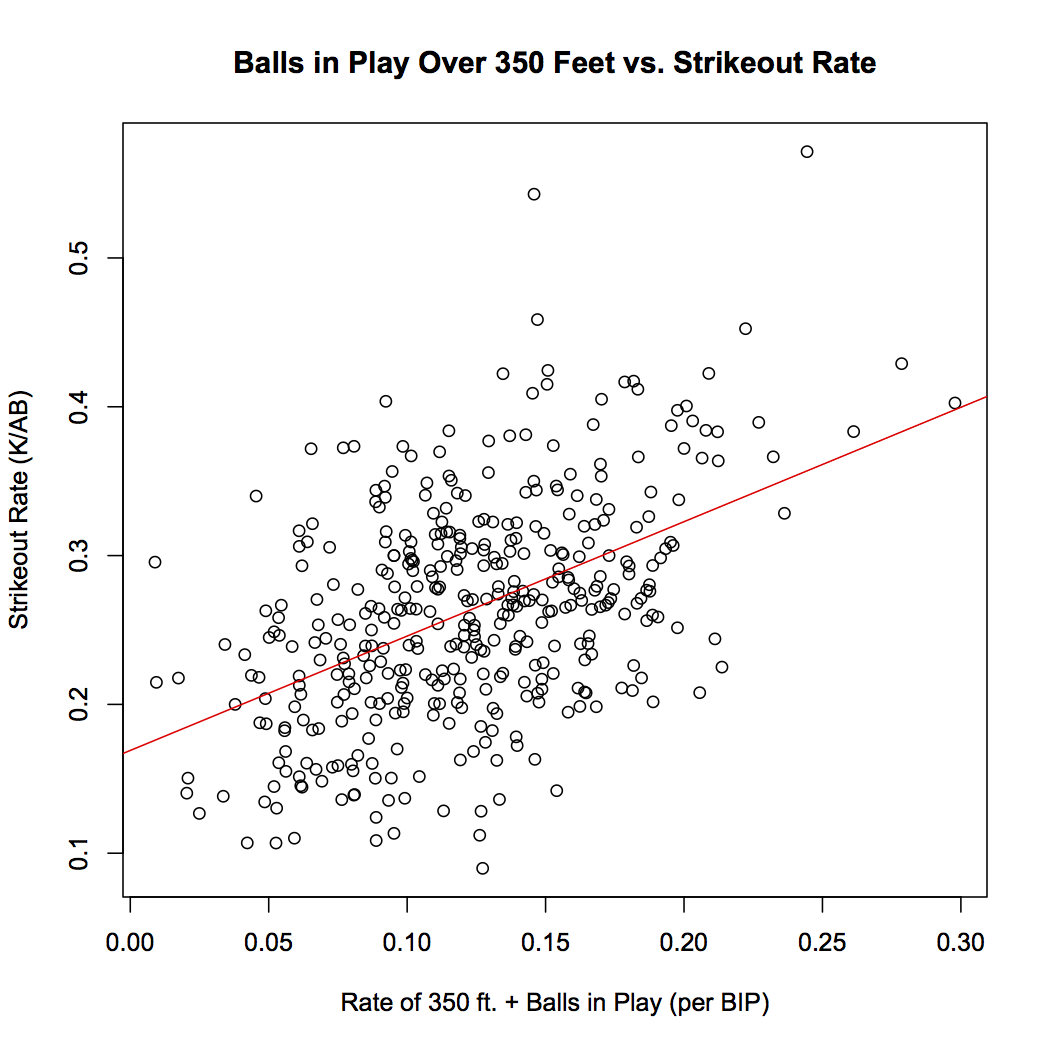
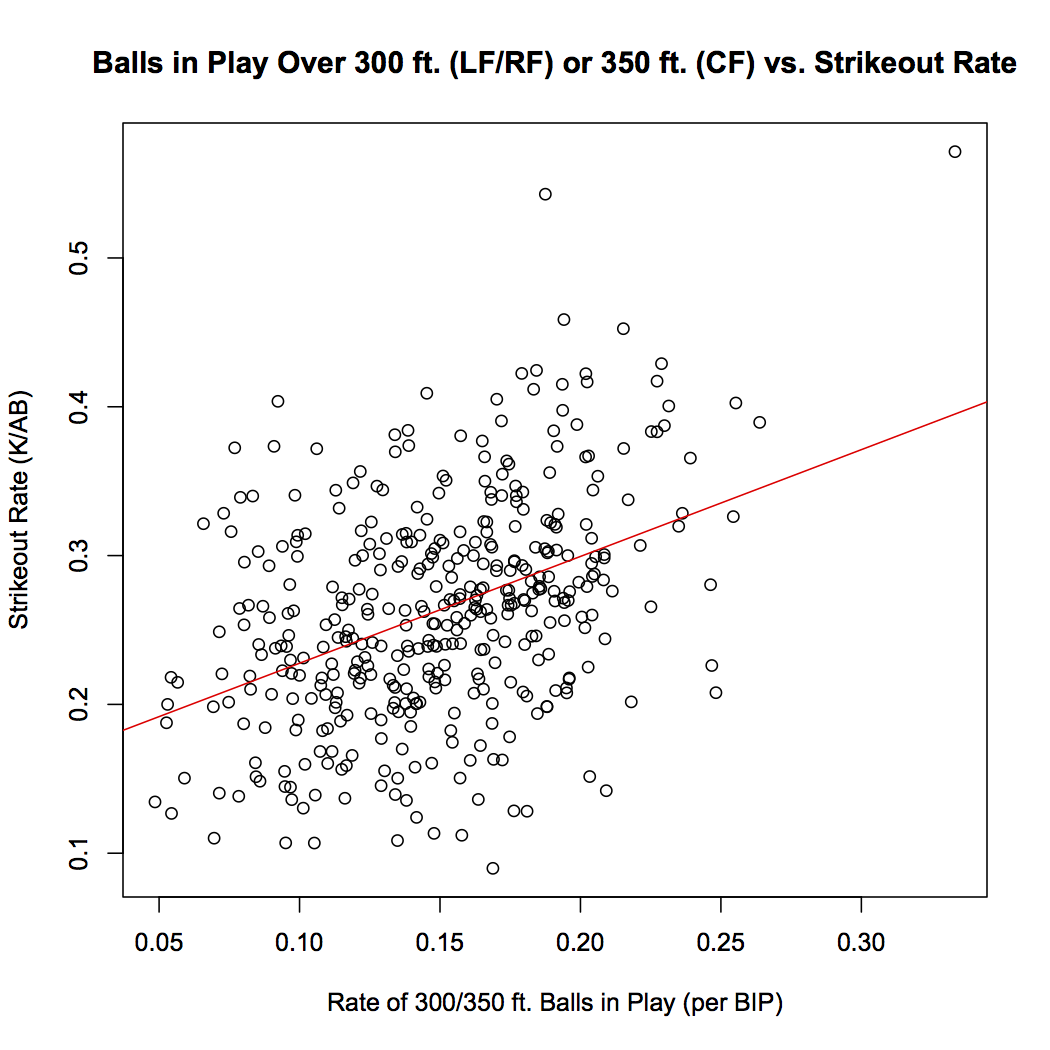
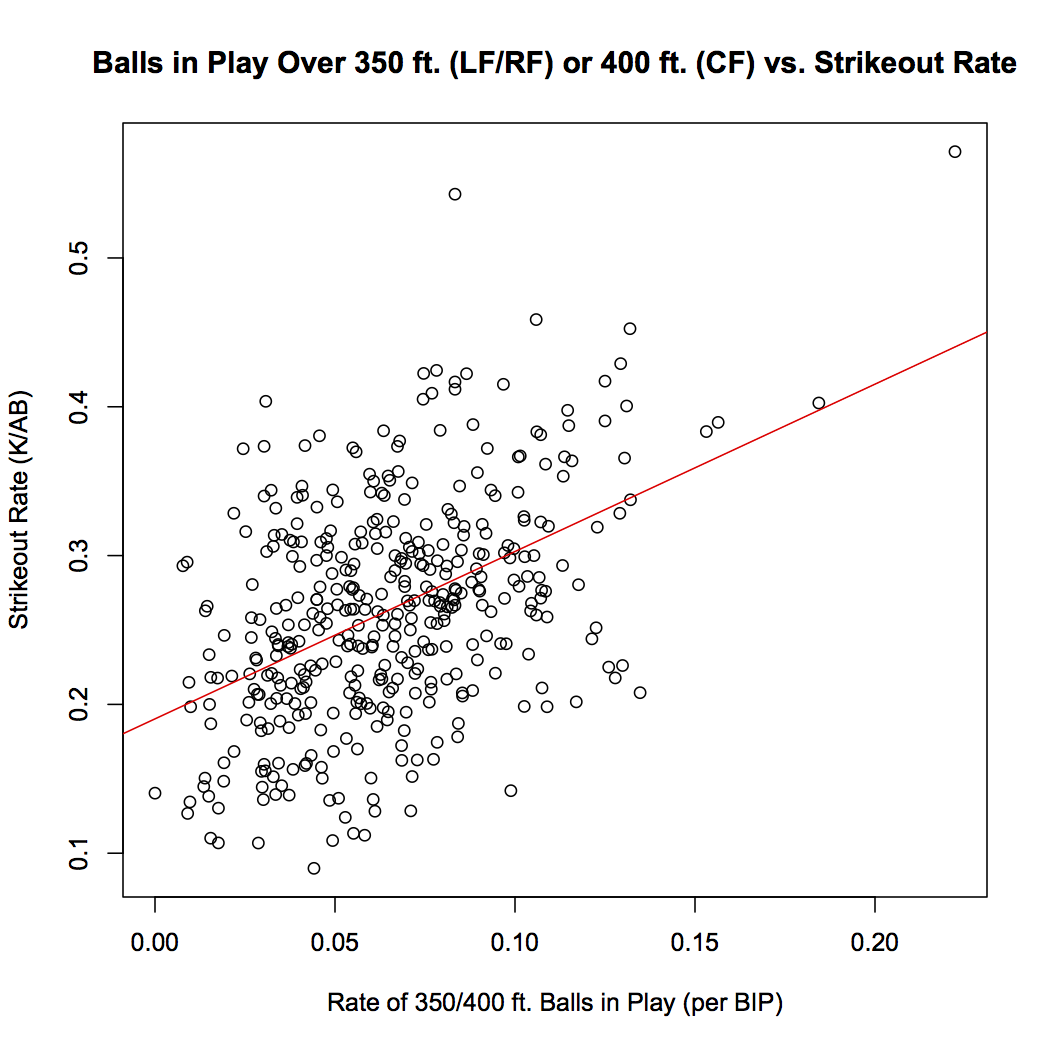
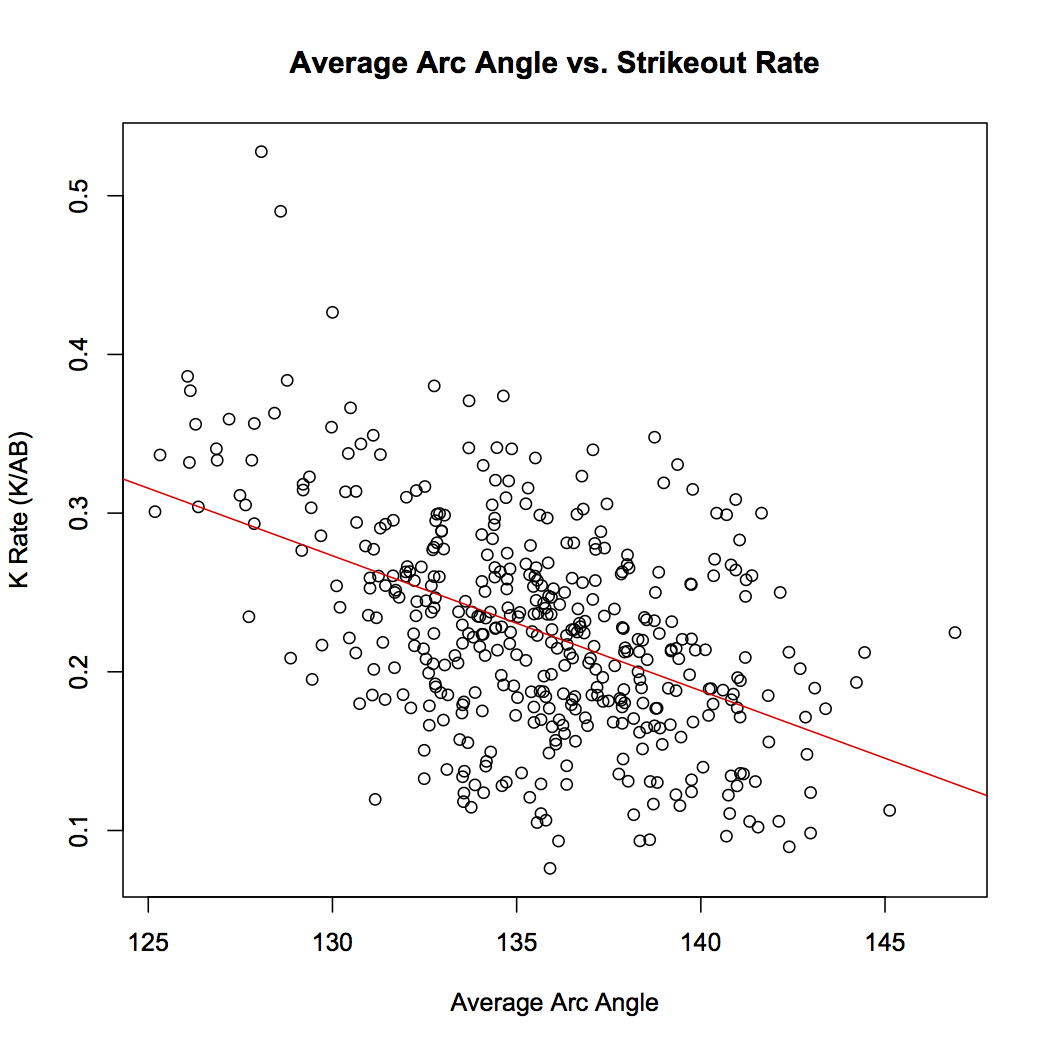
For many Minnesota Twins fans, the recently vintage dominance of the AL Central that spanned seemingly the entirety of the first decade of the 2000s had been taken for granted. I, for one, am guilty of this, and like many fans, am starting realize that winning is not easy, although the Twins made it seem as easy as Torii Hunter made robbing home runs look effortless. Nostalgia aside, the Twins, and their fall toward mediocrity, are an interesting topic to look into. To some, they seemed a similar team to the Oakland Athletics (perhaps aiding in the creation of a post-season rivalry). The Twins, who were not quite as much of a small-market team as Oakland, seemed to develop from within. They had a deep minor system, so deep that when Johan Santana or Torii Hunter deemed it time to cash in, the Twins were able to find a quick replacement and continue their success. Santana, and Hunter, as well as Joe Mauer and Justin Morneau (who have both had their careers altered due to more recent concussions) and many other corner pieces, all made their debut in a Twins uniform and became cornerstones, yet they could never win the big playoff series.

They did not have the ability to flex the financial muscle that the Red Sox, Yankees, and even division rivals Detroit Tigers were capable of; however, they still managed to win the AL Central six out of the 10 years in the previous decade, including a loss in a playoff game to decide the division winner in 2008. The success carried into the Target Field era, represented by a beautiful ballpark that fans spent what seems like an eternity waiting for. After another disappointing playoff loss to the hated Yankees, the Twins entered 2011 looking to improve, with a similar roster and the intrigue of Japanese second baseman, Tsuyoshi Nishioka. That year was filled with injuries, and despite a post-All-Star Game push, the Twins ended the year with the worst record in the American League. Since then, the Twins have failed to reach the playoffs, and are currently battling with the Atlanta Braves for the worst record in baseball. Not to mention, long-time general manager Terry Ryan, the one credited with building the farm system leading to the team’s prior success, was fired on July 18^th. Time to find out where the Twins went wrong.

Those successful Twins teams were always credited for their small-ball and defensive skills. With Joe Mauer behind the plate, Torii Hunter (replaced by Carlos Gomez, who could also flash some leather) and many other solid defenders manning the diamond, a lot of the Twins’ success was credited to this defense.

Yet the Twins were far from a one-dimensional team. The Twins had a solid pitching staff, including, most famously, Johan Santana, who was a two-time Cy Young winner with the club, before being sent off to New York. The Twins also produced one of the most exciting pitching prospects at the time in Francisco Liriano. Liriano’s career was marred by injuries, which led to his inconsistency. Despite Johan’s departure and Liriano’s ineffectiveness, the Twins’ pitching was still an effective unit. The Twins raised their pitchers not on the attractive strikeouts, but on “pitching to contact.” The premise behind this was that pitchers would attack the lower half of the strike zone, induce weak contact, and show excellent control to give up few walks. It seemed to work, as pitchers with low to average strikeout rates were able to be effective pitchers, such as Scott Baker, Nick Blackburn, Kevin Slowey, and Brian Duensing.

Before I delve into my research, I should point to Voros McCracken’s ideas about Defense Independent Pitching for those less sabermetrically inclined (if you are sabermetrically inclined, feel free to skip the next few paragraphs). If I were to give a brief summary of his work, I would say McCracken’s main point is that if a pitcher does not give up a home run or strike out or walk a batter, then he has little control of what happens to the batted ball in play. A lot of what happens can be credited to luck, sequencing, and how good his defense is. For those unaware of sequencing, it is the idea that if a pitcher gave up three singles and a home run in an inning, there are many different possibilities of what could happen. The three singles could come in a row, followed by the dinger, for a total of four runs, or, two singles could come early, the pitcher gets a double play or some other way to get out of the jam, then gives up a home run with the bases empty, followed by another single and an out. In that scenario, only one run was surrendered, despite an equal amount of hits. McCracken suggests there is randomness in this effect, which combined with the quality of defense behind the pitcher and a good deal of luck, can make ERA a poor indicator of a pitchers true skill.

McCracken looked at defense-independent pitching stats (HR, BB, K) and defense-dependent stats (ERA), and noticed that the defense-independent stats correlate much better from year to year, and are a better indicator of how a pitcher will perform, since a pitcher does not have control of what happens to balls in play.

While McCracken did not actually create FIP, his work was a building block for modern pitching analysis. FIP (Fielding Independent Pitching) tracks what a pitcher’s stats would look like if he played behind a league-average defense and experienced league-average luck. It is a much better indicator of future performance than ERA. All the data I used was from 2007-2014. Over that span, for pitchers who pitched more than 100 innings in at least a two-year span, a pitcher’s ERA from one year to the next (tracking how consistent the stat is in tracking performance) had a correlation coefficient of 0.338. FIP, conversely, had a correlation coefficient of 0.476. Clearly, FIP performs better when predicting future performance, as McCracken suggested.

To end my digression on McCracken’s importance, if I had to sum up its importance to this article, it is that pitchers have little or no control over what happens to a ball in play.

When I was talking Twins recently with some recent, justifiably uneasy Twins fans, they attributed the Twins’ recent troubles to injuries and inconsistent pitching. This was when I was reminded of the “pitch to contact” philosophy heralded by the Twins. Since the days of recently past successes, the Twins have changed management, and hopefully have let go of this ideology. Anyways, I thought to myself that McCracken’s work and subsequent furthering of the topic do not go along with the pitch-to-contact philosophy. Sure, if a pitcher can prevent walks and home runs, then it does go along with part of McCracken’s ideas. But, if the goal is to induce weak contact, yet the pitcher does not have control of what happens to a ball when it is contacted, then there is a bit of a discrepancy.

So, like any other statistically-oriented college mind looking for how to spend the rainy days of my summer break, I decided to run some regressions to test if “pitch to contact” actually succeeded and the Twins were able to induce weak contact, or if the relative success of the pitching staff is related to luck and a good defense.

To reiterate, the data I looked at came from the seasons of 2007-2014. To sum up the Twins’ pitching through the period, the period starts with solid pitching from guys who lack the ability to post high strikeout rates, excluding the one season Santana pitched in the study. Guys like Scott Baker and Nick Blackburn had solid seasons early on, but Blackburn and many others faded once things went downhill for the team. From the outside looking in, it may seem like a chicken-or-the-egg scenario, whether it was pitching that caused the downfall or some other factor that caused the pitching to fail.

I gathered data for Twins pitching over this span, and compared it to the rest of the league. The pitch-to-contact philosophy was easily visible, as over this eight-year span, only five Twins pitchers had higher strikeouts per nine innings than league average (Johan Santana, Phil Hughes, Scott Baker, Francsico Liriano, Kevin Slowey). At the same time, only four pitchers had a walks per nine innings above league average (Nick Blackburn, Boof Bonser, Sam Deduno, and Liriano), and most of those seasons came in that pitcher’s last season with the team. The data shows that despite few strikeouts, Twins pitchers found some success in limiting numbers of walks. However, for those pitchers who struggled with control, their combined ERA in those seasons was 4.82, with a FIP of 4.60. Clearly, if a pitcher struggled with control, their success was hindered by the high walk rate.

Much of the Twins’ pitching was inconsistent over this time as well, as pitchers such like Blackburn or Brian Duensing seemingly went from quality starters to below-average pitchers. For the most part, I found this to be a team-wide theme. For pitchers with multiple years with the club, I correlated year-by-year ERA and FIP, to see if any consistent trends arose. Amazingly, there was no correlation from ERA from one year to the next, as the R-squared value was 0.002, stressing no relationship at all (graph). FIP, on the other hand, showed an R-squared value of 0.15; so while not a concrete relationship, a weak relationship exists (graph).

Why this lack of consistent ERA and FIP? This is where I think BABIP comes into play. Since FIP does not take into account BABIP, it did produce more reliable data. A few outliers threw off the data, and since it is not a large sample size, those outliers did affect correlation. By the nature of the relationship, this probably did more to affect the FIP correlation than the ERA, but nonetheless, the small sample size of pitchers from this period did affect the relationship. Interestingly, but perhaps not surprisingly, I performed a regression graphing FIP to ERA, and a solid relationship exists, with an R-squared of 0.36 (graph). This would be even better of a correlation if I took out seasons by Phil Hughes and Liriano, as in those two seasons their FIP was almost a full point lower than their ERA, respectively. This shows the validity of FIP as a metric, as it accurately predicts how a pitcher likely will perform based on independent factors.

Nonetheless, there is a clear difference here in the two pitching metrics. FIP implies a relationship, while ERA does not. How can this be? My theory is that it has to do with the pitch-to-contact philosophy. If pitchers are constantly relying on luck and defense to produce outs, rather than getting batters out themselves, then random variation will play much greater of a role in a pitcher’s effectiveness. Additionally, a team’s defense will play much greater of a role in pitching.

How much can a defense affect pitching? Well, I graphed the total WAR produced by the various Twins defenses against the team ERA from the 2007-2014 seasons. I additionally graphed BABIP against team defense. Amazingly, an ERA to defense regression produces an R-squared of 0.47 (graph), while a Defense to BABIP regression produces a 0.37 R-squared value (graph). Team defense clearly has a relationship with team ERA and team BABIP, as when the Twins defense was in its prime (2007, 2010), pitching performed well. Similarly, in the defense’s worst two seasons, the team also had its highest BABIP (2013, 2014). For those wondering, FIP to team defense produces no correlation (as we expect, since it does not account for a team’s defense) with an R-squared of 0.003.

What does this all mean?

Putting it all together, we notice a few trends. After 2010, the defense took significant steps back, along with pitching (ERA). As we expect, the team’s BABIP was affected by the defense’s regression. FIP, on the other hand, remained fairly constant through the span, showing how the defense must play a role in team ERA. For example, we will look at 2014. This was the defense’s worst year in the span, with a defensive WAR of -46.5. Team ERA was second-worst in this year, at 4.58. FIP, conversely, showed the team had its second-best year in pitching, with a value of 3.97. This shows that if the Twins would have had an average defense, their ERA would have been much lower.

As team ERA ballooned, the quality of the Twins’ defense fell. Since Twins pitchers were taught to rely on their defense through the pitch-to-contact ideology, this relationship was amplified. Pitching to contact, although relying on luck and defense, may have had some merit when the Twins’ defense was in its prime. If the team could get to more balls, produce a few more outs, then as long as the pitchers kept batters from getting on for free via the walk, the team would succeed. The pitcher would not need to strike out as many batters since the defense would make more outs than the normal team. This sounds nice on paper, but as the team defense decayed, the pitching regressed. This is most evident in 2014, as a solid pitching staff was marred by the defense behind them.

If the Twins were to truly focus on pitching to contact, then they should have looked at the defense, not the pitcher. At the same time, pitching to contact is flawed in a way. Why should a pitcher rely on a defense if he can just get the batter out himself? Teaching a pitcher not to use his natural talent to strike out a batter is counter-productive. I am not saying the Twins’ coaching staff directly did this, but when only four pitchers in an eight-year span have above-average strikeout rates, it raises the question. Perhaps the Twins looked for pitchers who were undervalued because of their low strikeout rates, and used these undervalued pitchers in their pitch-to-contact system. Yet, this does not seem to be the case, as the Twins pitchers with the lowest ERAs and FIPs were the pitchers with the highest strikeout rate, excluding Brian Duensing, whose downfall could have been predicted by his 3.82 FIP (to a degree), as it showed is 2.62 ERA would be much closer to 4.00 with an average defense. Even in a pitch-to-contact system, the pitchers with the best ability to get the batter out without putting the ball in play were the best pitchers.

If pitching to contact were to have a textbook year, it would be 2007, where a team with a 4.37 FIP had an ERA of 4.18. Yet, soon after, the defense plummeted, bringing the team pitching down with it. Clearly, through the team’s porous defense, the Twins gave up on pitching to contact, too. They just hadn’t realized it yet.

Hopefully, with the new management in place, pitching to contact is forgotten. While it is also important to keep a viable defense behind the pitcher, I still can’t trust the pitch-to-contact ideology. It had a good run, but seriously, when was the last time the Twins were able to produce a consistent pitcher out of a highly-praised prospect? Liriano wasn’t consistent, Kyle Gibson has yet to dominate, and Jose Berrios has looked shaky is his brief appearances. I think Scott Baker might be the answer to my question, but if not him, then maybe Johan Santana?

Clearly, the Twins need a new philosophy for grooming pitching. It’s a team riddled with questions, and this is not the lone answer, but it can be one step in the right direction for the team currently pegged at the bottom of the AL barrel.

In “Hardball Retrospective: Evaluating Scouting and Development Outcomes for the Modern-Era Franchises”, I placed every ballplayer in the modern era (from 1901-present) on their original team. I calculated revised standings for every season based entirely on the performance of each team’s “original” players. I discuss every team’s “original” players and seasons at length along with organizational performance with respect to the Amateur Draft (or First-Year Player Draft), amateur free agent signings and other methods of player acquisition.  Season standings, WAR and Win Shares totals for the “original” teams are compared against the “actual” team results to assess each franchise’s scouting, development and general management skills.

Expanding on my research for the book, the following series of articles will reveal the teams with the biggest single-season difference in the WAR and Win Shares for the “Original” vs. “Actual” rosters for every Major League organization. “Hardball Retrospective” is available in digital format on Amazon, Barnes and Noble, GooglePlay, iTunes and KoboBooks. The paperback edition is available on Amazon, Barnes and Noble and CreateSpace. Supplemental Statistics, Charts and Graphs along with a discussion forum are offered at TuataraSoftware.com.

Don Daglow (Intellivision World Series Major League Baseball, Earl Weaver Baseball, Tony LaRussa Baseball) contributed the foreword for Hardball Retrospective. The foreword and preview of my book are accessible here.

Terminology

OWAR – Wins Above Replacement for players on “original” teams

OWS – Win Shares for players on “original” teams

OPW% – Pythagorean Won-Loss record for the “original” teams

AWAR – Wins Above Replacement for players on “actual” teams

AWS – Win Shares for players on “actual” teams

APW% – Pythagorean Won-Loss record for the “actual” teams

Assessment

The 1904 Brooklyn Superbas 

OWAR: 36.2     OWS: 250     OPW%: .500     (77-77)

AWAR: 21.5      AWS: 167     APW%: .366     (56-97)

WARdiff: 14.7                        WSdiff: 83  

Brooklyn placed fifth in ’04 as the Giants battered the opposition en route to the National League pennant. The “Original” Superbas bettered the “Actuals” by 19 games. Fielder Jones registered 25 stolen bases and Jimmy Sheckard added 21 for Brooklyn. “Honest” John Anderson and Claude “Little All Right” Ritchey laced 12 three-base hits apiece. Rookie outfielder Harry “Judge” Lumley paced the League with 18 triples and 9 home runs.

Jimmy Sheckard placed twenty-fourth among left fielders in the “The New Bill James Historical Baseball Abstract” top 100 player rankings. “Original” Superbas teammates listed in the “NBJHBA” top 100 rankings include Jimmy Sheckard (24^th-LF), Fielder Jones (41^st-RF), Claude Ritchey (59^th-2B) and John J. Anderson (86^th-LF).

  Original 1904 Superbas                                Actual 1904 Superbas

Harry Howell accrued 21 losses in spite of a 2.19 ERA and a WHIP of 1.048. Oscar “Flip Flap” Jones completed 38 of 41 starts and recorded a 17-25 mark with a 2.75 ERA. Jack Cronin contributed 12 wins in his final campaign along with an ERA of 2.70.

  Original 1904 Superbas                             Actual 1904 Superbas

Notable Transactions

Fielder Jones 

Before 1901 Season: Jumped from the Brooklyn Superbas to the Chicago White Sox. 

Claude Ritchey 

Before 1897 Season: Purchased by the Cincinnati Reds from the Brooklyn Bridegrooms for $500.

February 3, 1898: Traded by the Cincinnati Reds with Red Ehret and Dummy Hoy to the Louisville Colonels for Bill Hill.

December 8, 1899: Traded by the Louisville Colonels with Fred Clarke, Bert Cunningham, Mike Kelley, Tacks Latimer, Tommy Leach, Tom Messitt, Deacon Phillippe, Rube Waddell, Jack Wadsworth, Honus Wagner and Chief Zimmer to the Pittsburgh Pirates for Jack Chesbro, George Fox, Art Madison, John O’Brien and $25,000. 

John J. Anderson 

May 19, 1898: Sent to the Washington Senators by the Brooklyn Bridegrooms as part of a conditional deal.

September 21, 1898: Returned by the Washington Senators to the Brooklyn Bridegrooms as part of a conditional deal.

March 24, 1900: Purchased by Milwaukee (American) from the Brooklyn Superbas.

September 26, 1900: Drafted by the Brooklyn Superbas from Milwaukee (American) in the 1900 rule 5 draft.

February, 1901: Jumped from the Brooklyn Superbas to the Milwaukee Brewers. (Date given is approximate. Exact date is uncertain.)

October 6, 1903: Traded by the St. Louis Browns to the New York Highlanders for Jack O’Connor. 

Harry Howell

September, 1898: Purchased by the Brooklyn Bridegrooms from Meridan (Connecticut State).

March 11, 1899: Assigned to the Baltimore Orioles by the Brooklyn Superbas.

March, 1900: Assigned to the Brooklyn Superbas by the Baltimore Orioles.

Before 1901 Season: Jumped from the Brooklyn Superbas to the Baltimore Orioles.

Honorable Mention

The 1967 Los Angeles Dodgers 

OWAR: 45.4     OWS: 274     OPW%: .515     (83-79)

AWAR: 32.5       AWS: 218      APW%: .451    (73-89)

WARdiff: 12.9                        WSdiff: 56

The “Original” 1967 Dodgers placed fifth in the National League, 13 games behind the front-running Giants. Nevertheless the “Originals” outpaced the “Actuals” by a 10 game margin. Roberto Clemente (.357/23/110) collected his fourth batting crown, led the circuit with 209 base hits and secured the seventh of twelve consecutive Gold Glove Awards. Frank “Hondo” Howard dialed long distance 36 times. Maury Wills nabbed 29 bags and Tommy H. Davis scorched 32 doubles while producing matching batting averages at .302. Jim Merritt tallied 13 victories and delivered a 2.53 ERA along with a WHIP of 0.993. Don Drysdale equaled Merritt’s win total while fashioning an ERA of 2.74 with 196 strikeouts.

On Deck

What Might Have Been – The “Original” 1978 Pirates

References and Resources

Baseball America – Executive Database

Baseball-Reference

James, Bill. The New Bill James Historical Baseball Abstract. New York, NY.: The Free Press, 2001. Print.

James, Bill, with Jim Henzler. Win Shares. Morton Grove, Ill.: STATS, 2002. Print.

Retrosheet – Transactions Database

The information used here was obtained free of charge from and is copyrighted by Retrosheet. Interested parties may contact Retrosheet at “www.retrosheet.org”.

Seamheads – Baseball Gauge

Sean Lahman Baseball Archive

The Community Research section of FanGraphs serves as an excellent sounding board for aspiring amateurs (yes, those aspiring to rise to the level of amateur). After posting about a new statistical model or a detailed analysis of player performance, fellow Community Researchers are given a chance to chime in with helpful comments, sometimes leading to revision of previously drawn conclusions. More rarely, however, do the names that grace the upper sections of the website comment, but when they do, it always leads to revision.

Last week I published a new iteration of xHR, one that was drawn from xHR/BBE. It used four variables: FBLDEV, wFB/C, SLAVG, and FB%. In my naiveté, I neglected to properly analyze the variables I included in the regression model. As Mike Podhorzer helpfully pointed out, both wFB/C and SLAVG do not quite work as variables in the proper sense. Because they are heavily results-based and are both dependent on home runs for their results, they skew the math quite a bit for calculating how many home runs a player ought to have hit. It’s helpful to think of it in terms of calculating an xSLG. As Mr. Podhorzer put it, “It’s like coming up with an xSLG that utilizes doubles, triples, and home-run rates! Obviously they are all correlated, because they are part of the equation of SLG.”  They make for a sort of statistical circular logic.

For that reason, I came up with a different model, with the same basic objectives and two of the same variables, but getting rid of the improper variables. In this one, I used:

• AVG FBLDEV – Average fly ball/line-drive exit velocity. The idea is that the higher this value is, the harder the player is hitting the ball, and so he will hit more home runs.
• AVG FBDST – Average fly-ball distance. It’s rather intuitive because the farther a player hits fly balls, the more likely he is to hit home runs. If anything, like FBLDEV, it’s a clear demonstration of power. Obviously it has a decent correlation with FB%, but it isn’t necessarily tangled up with home-run results.
• K% – The classic profile of a home-run hitter is one who walks a lot, strikes out quite a bit, and hits balls that leave the yard. I suppose that a common conception is that the harder a player swings, the less control he has.
• FB% – Fly-ball percentage obviously figures pretty heavily into a power hitter’s profile. It’s awfully difficult to hit a lot of home runs without hitting a plethora of fly balls.

Without further ado, here’s the new xHR:

Note: To be clear, the end goal is not necessarily xHR/BBE, but rather xHR. xHR/BBE is just the best path to xHR because HR/BBE is a rate stat, meaning that it will have a better year-to-year correlation than home runs because that’s a counting stat. So if a player gets injured and only plays half a season, his HR/BBE would probably be similar to his career values, but his home-run numbers would not be. With that in mind, remember that the model was made for HR/BBE, not HR, so you will necessarily have “better” results if you’re looking for xHR/BBE.

Pretty good results, to be sure, even if it’s a bit worse than the prior version. A .7989 R-squared value is nothing to scoff at, especially if you think of it as the model explaining 80% of the variance. Clearly it still underestimates the better hitters, and that’s an issue, but there are really so few data points at the top that it’s hard to take it completely seriously up there. If there was a lot more data and it still did that, then I’d be inclined to either add a handicap or to think it ought to be a quadratic regression.

As always, the formula:

xHR= (.170102188*FB% -.014640853*K% + .0000269758*AVGDST + .005672306*FBLDEV -.541845681)*BBE

Even more than the previous version, this model is easily accessible to all fans because the variables are comprehensible. Moreover, it isn’t terribly difficult to head over to Statcast or Baseball Savant to obtain the relevant information and make the calculation. Anyway, I hope you enjoy and use this information to the fullest extent.

In “Hardball Retrospective: Evaluating Scouting and Development Outcomes for the Modern-Era Franchises”, I placed every ballplayer in the modern era (from 1901-present) on their original team. I calculated revised standings for every season based entirely on the performance of each team’s “original” players. I discuss every team’s “original” players and seasons at length along with organizational performance with respect to the Amateur Draft (or First-Year Player Draft), amateur free agent signings and other methods of player acquisition.  Season standings, WAR and Win Shares totals for the “original” teams are compared against the “actual” team results to assess each franchise’s scouting, development and general management skills.

Expanding on my research for the book, the following series of articles will reveal the teams with the biggest single-season difference in the WAR and Win Shares for the “Original” vs. “Actual” rosters for every Major League organization. “Hardball Retrospective” is available in digital format on Amazon, Barnes and Noble, GooglePlay, iTunes and KoboBooks. The paperback edition is available on Amazon, Barnes and Noble and CreateSpace. Supplemental Statistics, Charts and Graphs along with a discussion forum are offered at TuataraSoftware.com.

Don Daglow (Intellivision World Series Major League Baseball, Earl Weaver Baseball, Tony LaRussa Baseball) contributed the foreword for Hardball Retrospective. The foreword and preview of my book are accessible here.

Terminology

OWAR – Wins Above Replacement for players on “original” teams

OWS – Win Shares for players on “original” teams

OPW% – Pythagorean Won-Loss record for the “original” teams

AWAR – Wins Above Replacement for players on “actual” teams

AWS – Win Shares for players on “actual” teams

APW% – Pythagorean Won-Loss record for the “actual” teams

Assessment

The 1997 Boston Red Sox 

OWAR: 63.7     OWS: 317     OPW%: .583     (94-68)

AWAR: 41.4      AWS: 234     APW%: .481     (78-84)

WARdiff: 22.3                        WSdiff: 83  

The “Original” 1997 Red Sox cruised to the pennant by a ten-game margin over the Yankees. Jeff Bagwell delivered a 30/30 season (43 HR / 31 SB), drove in a career-high 135 baserunners, rapped 40 doubles and coaxed 127 walks. Brady Anderson followed his 50-home run campaign in ’96 with 39 two-base knocks and 18 dingers. A trio of “Original” and “Actual” Sox infielders provided additional firepower in Boston’s stacked lineup. Nomar Garciaparra (.306/30/98) merited the 1997 AL Rookie of the Year Award as he registered 209 base hits, 122 runs scored, 44 doubles, 11 triples and 22 stolen bases. Mo “Hit Dog” Vaughn slammed 35 circuit clouts and supplied a .315 BA. John Valentin (.306/18/77) led the League with 47 two-baggers.

1B Jeff Bagwell and 3B Wade Boggs placed fourth at their respective positions in the “The New Bill James Historical Baseball Abstract” top 100 player rankings. “Original” Red Sox teammates specified in the “NBJHBA” top 100 rankings include Roger Clemens (11th-P), Mo Vaughn (51st-1B), Brady Anderson (63rd-CF) and Ellis Burks (77th-CF).

  Original 1997 Red Sox                                                             Actual 1997 Red Sox

Roger Clemens (21-7, 2.05) collected the 1997 AL Cy Young Award while posting a personal-best with 292 whiffs. Curt Schilling (17-11, 2.97) overpowered the opposition with a career-high 319 strikeouts. Paul Quantrill furnished a 1.94 ERA in 77 relief appearances. Tom “Flash” Gordon notched 11 saves for the “Actuals”.

  Original 1997 Red Sox                            Actual 1997 Red Sox

Notable Transactions

Roger Clemens

November 5, 1996: Granted Free Agency.

December 13, 1996: Signed as a Free Agent with the Toronto Blue Jays.

Jeff Bagwell

August 30, 1990: Traded by the Boston Red Sox to the Houston Astros for Larry Andersen.

Brady Anderson 

July 29, 1988: Traded by the Boston Red Sox with Curt Schilling to the Baltimore Orioles for Mike Boddicker. 

Curt Schilling 

July 29, 1988: Traded by Boston Red Sox with Brady Anderson to the Baltimore Orioles in exchange for Mike Boddicker.

January 10, 1991: Traded by Baltimore Orioles with Pete Harnisch and Steve Finley to the Houston Astros in exchange for Glenn Davis.

April 2, 1992: Traded by Houston Astros to Philadelphia Phillies in exchange for Jason Grimsley.

December 20, 1995: Granted free agency.

December 21, 1995: Signed by Philadelphia Phillies.

Honorable Mention

The 1927 Boston Red Sox 

OWAR: 32.6     OWS: 230     OPW%: .463     (71-83)

AWAR: 13.7       AWS: 153      APW%: .331    (51-103)

WARdiff: 18.9                        WSdiff: 77

The “Original” 1927 Red Sox tied for last place with the Indians yet managed to finish 20 games better than the “Actual” squad. Babe Ruth (.356/60/165) established the single-season home run record and paced the Junior Circuit with 158 runs scored, 137 walks, a .486 OBP and a .772 SLG. Tris Speaker sported a .327 BA and laced 43 two-base hits in his penultimate season.

On Deck

What Might Have Been – The “Original” 1904 Superbas

References and Resources

Baseball America – Executive Database

Baseball-Reference

James, Bill. The New Bill James Historical Baseball Abstract. New York, NY.: The Free Press, 2001. Print.

James, Bill, with Jim Henzler. Win Shares. Morton Grove, Ill.: STATS, 2002. Print.

Retrosheet – Transactions Database

The information used here was obtained free of charge from and is copyrighted by Retrosheet. Interested parties may contact Retrosheet at “www.retrosheet.org”.

Seamheads – Baseball Gauge

Sean Lahman Baseball Archive

RotoGraphs, in addition to several Community writers, have been posting about an “x” category of metrics for quite some time. They include things like Andrew Dominijanni’s xISO, Andrew Perpetua’s xBABIP, and more. The clear purpose of developing those statistical indicators was to measure and predict fantasy-baseball success, something we all aspire to in our hopefully low-priced leagues (although you probably found that using x-stats is a lot like overstudying for a test because the amount of effort you put into preparing yields diminishing returns, and you “over-Xed” the players).

One of the most prominent of the x-stats trotted out at the beginning of every season is xHR/FB, developed by Mike Podhorzer, and always accompanied by an amusing “leaders and laggards” piece. His version of xHR/FB is quite good, with a .649 R-squared value. In his regression analysis, Mr. Podhorzer utilizes somewhat exclusive metrics (hopefully public at some point), such as average absolute angle. Overall, it’s a pretty good predictor, and it becomes doubly understandable to the layman when it gets multiplied by fly balls to produce an expected home-run value.

The only real issue I have with HR/FB (and its prediction) is that it is HR/FB. While it is more stable for hitters than for pitchers, it still isn’t quite as stable as a stat I’d like to use for fantasy baseball. For my 1000 player-season sample from 2009-2015, HR/FB had a year-to-year R-squared value of .49. It isn’t terribly difficult to figure out why. There are numerous reasons, including weather changes, team changes, opponent changes, player development, and more. Moreover, it doesn’t take a very good picture of a hitter’s overall profile because it only looks at how many home runs a player hits per fly ball. A player might have a high HR/FB, but he may not hit enough fly balls for the metric to accurately describe his power (i.e. whether he actually hit a lot of home runs). On the other hand, it’s important to note that a high HR/FB generally goes with a higher FB%.

Perhaps a better metric for evaluating a player in the greater context of his hitting profile is HR/BBE. Home runs per batted-ball event is just HR/(AB+SF+SH-SO). It has a slightly higher year-to-year R-squared of .56 (from my sample), in large part because it takes into account more variables than does HR/FB. Under the umbrella of BBE fall not only fly balls, but line drives (and there can be line-drive home runs), and ground balls. In case you’re wondering why I included sacrifice hits, it’s because they tell a little bit about what kind of hitter a player is. Most modern managers are far more likely to ask a Ben Revere to lay down a sacrifice bunt than they are a Kris Bryant.

And so I thought it might be useful to run a linear regression analysis to develop an xHR/BBE (and from there, xHR). I’m a statistical autodidact, so I tried to keep things simple. Additionally, I thought it would be best if I utilized accessible variables like FB% so that a moderately literate sabermetrician could use it. After testing myriad variables, I came up with four that I’d use — average FBLDEV (Statcast), wFB/C, SLAVG, and FB%.

• AVG FBLDEV – Average fly ball/line-drive exit velocity. The idea is that the higher this value is, the harder the player is hitting the ball, and so he will hit more home runs.
• wFB/C – A rather obscure metric buried in the FanGraphs glossary, wFB/C is weighted fastball run values per 100 pitches. I use it because most home runs come off some form of a fastball, and home-run-hitter types are typically good fastball hitters.
• SLAVG – “Slap” average, a metric of my own invention (although someone else has probably thought of it – I just haven’t seen it before), is singles divided by at-bats. It’s a bit like ISO in that it tells you about a player’s power distribution (or lack thereof). I figure that this is inversely correlated with power because the more singles a player hits, the fewer home runs he’s likely to hit.
• FB% – Fly ball percentage obviously figures pretty heavily into a power hitter’s profile. It’s awfully difficult to hit a lot of home runs without hitting a plethora of fly balls.

It seems like a decent list of predictors in that they are understandable and accessible to the average fan, in addition to having a good relation to home-run hitters. I used all players that had at least 100 batted-ball events in 2015 and 2016 (Statcast only has data going back to 2015), which turns out to be close to 500 player-seasons. So let’s throw them into the Microsoft Excel Regression grinder and see what it spits out:

Note: To be clear, the end goal is not necessarily xHR/BBE, but rather xHR. xHR/BBE is just the best path to xHR because HR/BBE is a rate stat, meaning that it will have a better year-to-year correlation than home runs because that’s a counting stat. So if a player gets injured and only plays half a season, his HR/BBE would probably be similar to his career values, but his home-run numbers would not be.

The primary thing to recognize here is the R-squared value: a pretty good .78272. To the uninitiated, this simply means that the model explains 78% of the HR variance. If you’re interested (and you really ought to be), here are the coefficients for the variables and the overall formula:

xHR= (.114557524*FB% – .183885205*SLAVG + .006658976*wFB/C + .004075449*FBLDEV -.343193723) * BBE

With this information, it isn’t terribly difficult to look up a few pieces of data on FanGraphs and Statcast to see how many home runs a player “should” have hit. In case you’re wondering about its predictive value relative to that of HR/BBE, xHR/BBE has an R-square value that’s six points higher (.61). Nevertheless, it’s important to note that, based on the graph, the model struggles to predict home-run numbers for the players on the extremes – the Jose Bautistas of the world. Because the linear regression tends to underestimate rather than overestimate at the top, it’s likely that a quadratic regression would fit better. It’s something to look into, but this’ll do for now. Moreover, while there are some really crazy outliers, like Jose Bautista being predicted to hit 12 fewer home runs (Steamer does have him on pace for only 26 this year!), the model does work reasonably well for more average players.

Keep in mind that numerous improvements will be made. If anyone wants access to data or has a question, then just let me know. If not, then enjoy the tool and use it for fantasy, even though it’s getting a bit late for that. Maybe next year.

In this post, I take a look at the 2016 Chicago Cubs though their first 100 games. I’ll start out by focusing on the Cubs’ run differential (Runs Scored – Runs Allowed). After a historic start, they reached their pinnacle after the 67th game of the year against the Pirates. At this point, the Cubs were 47-20 and had outscored opponents by 171 runs! Since then, the ball club is 13-20 and their current run differential is at +153.

Still, the Cubs’ +153 mark is 42 runs better than the next-closest team (Washington Nationals). The Cubs and Nationals are the only clubs to have a run differential that is greater than +100. The second-place Cardinals rank third in the league at +95 right now. While the Cubs dominate the top end of the spectrum, the Reds and Braves are running away with the worst run differentials in the league. The Reds have a -143 mark, largely due to the thrashings they have taken at the hands of the Cubs so far in 2016. The Braves have the second-to-worst differential at -134 runs.

Projected Runs to Wins

In another place, I introduced the “Pythagorean Theorem’s of Baseball” which basically tries to determine the number of games a team will win based on their number of runs scored and number of runs allowed. Here are the formulas for six of the most common win-percentage projection formulas:

I added up the Cubs’ total runs scored and total runs allowed after each game this year and compared their actual number of wins to the projected number of wins based on each formula. These charts visualize the differences between those numbers.

This matrix summarizes how accurate each of the projection formulas has been in predicting the Cubs’ winning percentage and total number of wins so far in 2016. The most accurate formulas was the James_1.83 followed by the James_2 and Soolman. Four of the six formulas were very good predictors, but the Cook and Kross formulas overforecasted the number of wins that they expected the Cubs to have. Notice that at one point this year, each of those formulas projected the Cubs to have over 15 more wins than they actually had. The R^2 value (coefficient of determination) is indicative of how well the projected win percentage matched up to the actual win percentage after each game this season.

All in all, the Cubs have should have at least six more wins this year based on these formulas. Scoring as many runs as they have (4th most in the MLB) and allowing as few runs as they have (T-1st in the MLB) should result in an even better record than 60-40. We knew it was unlikely that they would keep up their record-setting start in the run-differential category, but it will be interesting to see how these numbers match up as the season progresses.

Well, here we are: Over 100 games into the season and Bryce Harper has yet to break out of his slump. When Bryce came to the Majors back in 2012 he was one of the most hyped prospects since Alex Rodriguez broke into the bigs as a 19-year-old shortstop. The pressure, I’m sure, was immense, and through his first three seasons Harper had put up good numbers, but had yet to establish himself as the superstar we all thought he’d be. Something clicked in 2015 though, as he posted an amazing 9.5 WAR, 197 wRC+, and 0.461 wOBA, all best in the MLB by a fair margin. We all thought he’d done it, he had exceeded expectations and was ready to join Mike Trout as one of the most exciting, talented, and productive players in the game. His 1.5 WAR, 180 wRC+, and 0.443 wOBA through April of 2016 merely affirmed this sentiment.

Here we are. 2.8 WAR, 115 wRC+, and 0.346 wOBA. To be fair, these are by no means terrible numbers. He is still creating runs at a decently better rate than the average MLB player, with much of the credit going towards his MLB-leading 18.2 BB% and his 0.214 ISO. His defense has also been very good this year, helping to raise his WAR to 41st in the MLB. No, I am not saying Harper is a bad player, I’m just saying he is worse than the Bryce Harper we saw in 2015. We were all ready to call him a superstar (heck, we even voted him into a starting spot at this year’s All-Star Game), but now he’s taken this step back and we have no choice now but to start questioning his superstar status. Let’s take a look both at what might be causing this slump, and what Bryce could do to bust out of it (if anything at all).

The stat that jumps out at me most is his BABIP. The MLB average is exactly 0.300 this year, and Bryce has a career mark of 0.317. Bryce isn’t too far into his career, and while it’s possible that his 0.369 BABIP last season was an anomaly, it’s certainly safe to say that Bryce is definitively above average in this area. This season his BABIP has dipped down to 0.234, good enough for second to last in the MLB, ahead of only Todd Frazier (0.203). BABIP has a great degree of luck involved, in that some hitters with higher BABIPs might just get lucky (e.g. hit a little bloop into shallow right field that drops for a hit), or might be playing poor defenses (e.g. Jason Heyward would have caught that little bloop, but Jose Bautista was in right field and missed it by a foot). I believe, though, that going from 0.369 in 2015 to 0.234 in 2016 is enough of a differential to at least form the hypothesis that Bryce is struggling beyond just facing better defenses and getting less breaks.

One of the keys to figuring out this drop in production is figuring out what has changed from last year. Obviously his BABIP has declined, but why? For the  most part, pitchers are throwing him the same types of pitches at the same rates, and are throwing pitches in/out of the zone at the same rates as well. He has almost the exact same swing% on pitches outside the zone, but there’s about a 5% decrease in his swing% on pitches in the zone; nothing monumental, but something we ought take note of. The greatest changes that may be observed are in his batted ball numbers, shown here:

We can almost construct a narrative from these numbers: He’s hitting balls soft significantly more often, and he’s also hitting less line drives. Soft ground balls and fly balls are easier to convert into outs, and his infield fly ball% increase implies that he is hitting fly balls with less power. This explains why his home run rate is down. Where he was previously hitting hard line drives and grounders, and turning fly balls into home runs, he is now hitting softer, more easily-fielded grounders and popups, resulting in a steep decline in BABIP.

But this isn’t a cause, it’s a symptom. Again, we are forced to ask why it is that Bryce isn’t hitting balls as hard, and why he’s hitting less line drives? Bryce has been known for having great plate discipline, something that generally hasn’t changed over the last two years. At the surface, we see that he still has a very high walk rate, lays off pitches outside of the zone, and is one of the more patient hitters in baseball. However, one stat that caught my eye was his contact% on pitches outside the zone (and even inside the zone). His O-contact% went from 60.9% to 67.4%, and even his Z-contact% increased from 84.4% to 87.7%. This can be visualized here:

For the 2015 season

And for the 2016 season

There are two ways to look at this: The types of pitches Bryce is seeing, and the counts he’s getting himself into. All of this revolves around where pitchers are throwing pitches, where he’s swinging, and where he’s making contact. As you can clearly see, Bryce has been making a tangibly higher amount of contact this season. Logically, it makes sense to say that he is taking more pitches in the zone, and making weak contact where he used to just swing and miss. But that can’t be the whole story, can it? In attempting to find differences between this season and last, I merely found that regardless of what the count was, Harper was always making more contact; it didn’t matter if he was ahead, behind, or even. He was also making more contact regardless of what pitches were being thrown.

Let’s start with the types of pitches Bryce sees. We’ll split it up into fastballs (which includes 4-seamers, 2-seamers, and cutters), and secondary pitches (curveballs, sliders, and changeups). With secondary pitches, pitchers have begun to come into the zone a bit more than they used to. These charts show where pitchers are throwing Bryce non-fastballs:

2015

2016

It is by no means a huge difference, but it’s still there. Obviously, pitchers are still mostly throwing him non-heaters down and away, they’re just getting them in the zone more frequently. How does Bryce respond to this change? Well, he’s been laying off the low pitch a bit more, and instead has attempted to hit the inside pitch. These are his swing percentages on secondary pitches:

2015

2016

This also means that those non-fastballs are being called as strikes more frequently (assuming that umpires are generally going to call pitches in the zone as strikes). As we can see in his contact% charts, this season Bryce has been making contact at an extremely high rate on those high and inside pitches, and softer pitches have been absolutely no exception. In fact, he’s been making contact with the high and inside non-heaters more than he is with high and inside fastballs. What are the implications of this? Let’s look at his slugging% against secondary pitches:

2015

2016

Slugging% is by no means a perfect measure of a hitter’s ability. Yet, in this case, it gives us a decent idea of which locations a hitter is making solid contact. In his 2015 campaign he was able to get his arms extended and drive curveballs with great power. This season he is attempting to pull the ball more, and it’s resulting in weaker contact. While he is able to drive the inside breaking ball at a pretty decent rate, I suspect that he’s opening up his stance, which can occasionally result in a hard-hit ball, but will often result in a weak fly ball to the opposite field, or a weak grounder to the pull side. The fact that he’s swinging so much more frequently at inside pitches would also be reason to guess that as he’s swinging at breaking balls out over the plate he is still attempting to pull them, as opposed to going with the pitch. Further evidence of this comes from looking at how he hits breaking balls from lefties (curving away from him), versus how he hits them from righties (curving towards him).

2015

He even seems to do better against lefties. Against both of them, however, he clearly is able to see the pitch that will eventually break across the middle/outer half of the plate, and drive it with power. Let’s head over to 2016:

While his production has decreased against both righties and lefties, it is clear that the disparity is much larger when it comes to lefties. This is because Bryce is able to get away with trying to pull the ball against righties, as the ball is curving towards him. This makes pulling the ball a much more natural motion. Against lefties, the only breaking balls he is hitting are the ones that start inside and break right to the inside part of the plate, and the pitches that break to be right down the middle. It is the non-fastballs that are low and on the outer part of the plate that he is unable to drive, especially the ones being thrown by lefties. He’s opening up more, which also explains why his pull% hasn’t gone up (in fact it’s gone down). When he’s open, it’s hard to drive the outside pitch even if you make contact with it intending to hit it to the opposite field. Instead, he’s making that weak contact that results in outs.

Looking solely at secondary pitches, the narrative becomes: Bryce is taking the pitches that are out over the plate, and is instead swinging at pitches that are high and inside. He has a tendency to attempt to open up to the ball, and while he can sometimes get away with it against righties, lefties have been able to essentially shut him down. He is also making much more contact with all of these pitches, meaning that he’s putting more balls in play, yes, but they are weak balls that are easy to field, and are thus resulting in outs. With this mindset, even trying to hit the ball to the opposite field becomes more difficult, and all of this culminates in a lower BABIP.

Next, let’s look at how he’s handling fastballs. One thing that quickly becomes evident is the fact that Harper has been swinging at fastballs a lot less this year, especially ones up in the zone.

2015

2016

His swing% on fastballs in other areas of the zone is roughly the same; it’s really just those high and down-the-middle fastballs that he’s suddenly laying off of more. And yet, just as with non-fastballs, Harper still has been managing to make more contact this year, especially on pitches high and inside, as well as pitches low and out of the zone. How has that translated in terms of his slugging%?

2015

2016

What immediately jumps out at you is the large hole in the top part of the zone this year where Bryce is generating virtually no production. His production on low fastballs is closer to on par with last season, but up in the zone (the same area where he isn’t swinging nearly as often) he can’t get anything going. Why is this? With fastballs it’s a little more simple than with breaking balls in some aspects: For whatever reason he’s laying off fastballs in the zone, and he’s making weak contact with fastballs both high and inside, and down and away (which is where pitchers throw him fastballs most frequently). He’s giving pitchers more opportunities to throw fastballs out of the zone too. The big question mark comes at why he can’t do anything with those high fastballs specifically?

The answer isn’t too straightforward, but I do think that a large part of it is what types of pitches Bryce swings at in which counts. See, there is a very large differential in Bryce’s swing% in counts with no strikes between last year and this year, whereas in two-strike counts his swing% is about the same. He is taking more pitches when he has no strikes against him, especially the high fastball:

2015

2016

He seems to be swinging at less pitches overall, and his focus has shifted from the top of the zone to the inside part of the zone. It should be noted, too, that he is swinging significantly less at breaking pitches with no strikes as well, which highlights something that’s a little less tangible. With fastballs the narrative becomes this: Bryce is taking more fastballs early in the count, which means he isn’t capitalizing on those fastballs. Once he has two strikes on him, it would reason to guess that he would have more trouble making square contact, right? Well, not quite…

Against fastballs in two-strike counts Bryce is actually hitting decently, but he’s still missing the ones across the middle of the plate. One thing I noticed is that, in two-strike counts, he’s getting thrown more breaking pitches than before, and less fastballs. In 2015, 258 out of 719 two-strike pitches were breaking balls (36%). In 2016, the mark has been 189 out of 448 (42%). With two-strike pitches in 2015, 383 out of 719 were fastballs (53%), whereas 2016 has only seen 220 out of 448 (49%). Bryce has become more aware of the outside pitches, both fastballs and breaking balls, and this has something to do with it.

With two strikes, Bryce is swinging at around the same rate in 2016 as he was in 2015. The pitches he is hitting successfully are: High and inside fastballs, away fastballs, away breaking pitches from righties, all breaking pitches in the middle of the plate, and high and inside breaking pitches from lefties. Ok, that’s pretty tedious. Let’s show all of that visually, looking just at 2016:

First, fastballs with two strikes

Again, he’s gearing up for away pitches, and he’s swinging at almost anything, so he has success against away fastballs. We know that he’s been very keen on high and inside pitches of all kinds and in all counts this year, and that is also the easiest pitch to see. He has a reactionary eye for that pitch, and is able to catch up and drive it. High fastballs out over the plate can be somewhat easy to react to but he a) isn’t as keen on hitting them, b) isn’t seeing them that often in two-strike counts anyways, and c) isn’t expecting them. Thus, he’s most likely popping them up, which explains his high increased infield fly ball%. This is supported by the fact that his ground-ball rates on high fastballs with two strikes is quite low:

Next, let’s look at slugging% against breaking pitches from righties with two strikes

Again, it appears that because the ball is curving towards him it’s going to be easier to drive. He is then able to pull the breaking pitches that are up and out over the plate, and is able to drive the low and outside pitches with authority. His lack of success on up and away pitches is a little perplexing, but could be attributed to anything from bad luck, to him possibly not seeing that exact pitch as well, to the fact that the sample size here is pretty small and he hasn’t seen a ton of pitches in that area.

Finally, let’s check out breaking pitches from lefties

Nothing monumental in this aspect, especially as it’s not too different from how he hits breaking pitches against lefties in all counts. Regardless, it still fits our narrative as the up and inside pitches are right in his wheelhouse, and the pitches that breaking out over the plate are easier to hit than any other breaking pitch coming from a lefty.

Whew. That is a lot of heat maps to take in. Let’s review a bit: Bryce has a tendency to take more pitches early in the count, something he hasn’t done before. He’s also opening up, which makes him susceptible to breaking pitches and causing him to make weaker contact. The fact that he’s making more contact on pitches outside of the zone doesn’t help much either. He’s taking more fastballs as well, and once he has two strikes on him he’s seeing less of them, and is most likely expecting them less. He then begins to swing much more frequently, which actually reaps pretty good rewards, though there are some holes in his swing against certain pitches. He can’t get the high fastball, and struggles with breaking pitches against lefties. The result of all of this? Lower BABIP, lower wRC+, lower wOBA, you name it.

Obviously there are factors involved with this that go far beyond what heat maps and stats can show us. Baseball is an incredibly mental game, and once you realize you’re in a slump it can sometimes just drive you deeper into that slump. Statistics also can almost never tell the whole story, and as I mentioned earlier the sample size here is small enough that none of this is much of a predictor for future behavior. There’s a good chance that, on many of the situations mentioned above, Bryce has just gotten unlucky (or heck, maybe even lucky) and thus the heat map doesn’t reveal much. Overall though, when looking at everything in a holistic manner it allows us to construct an idea as to why Bryce is failing where he previously succeeded. We can never know everything for sure, but we know more than we did.

I’ve been hearing for months now that Bryce will be just fine, slumps happen to everyone, he will soon return to form, etc., and I’m not here to disagree with that. Although, I will ask (and I ought add that I am a big supporter of Bryce’s): What if he doesn’t break out of it? Odds are his 2015 will be one of the best seasons of his career, and 2016 (if it continues like this) will be one of his worst, and he will find himself somewhere in between for the rest of his career. It’s just that the deeper he drives himself into this rut the more compelled I am to find the source of problem as best I can, from a purely analytical standpoint.

Love him or hate him, the more that Bryce (and the many young superstars like him) thrives, the more baseball thrives.

(Note: All statistics and heat maps taken from Bryce’s page on FanGraphs.com)