Exploring the Top 155 Pitchers
Happy Holidays. A new year is almost upon us. Just around the corner, pitchers and catchers will be gearing up to report. Spring-training facilities are prepping for an early start in anticipation of the World Baseball Classic, added excitement for any baseball fan ready to brush the cold off. Every new year brings change. Some more than others. This year, the new CBA was agreed upon. As the real game changes, so too does the fantasy world. Our league is entering its twelfth year, which is mind-blowing to me, considering we now represent six different states in four different time zones. Part of our longevity is attributed to adapting to the ever-changing landscape of baseball. Sabermetrics are slowing creeping into our stat categories — power is relied on less, and relievers more so. All that to say, we have changed again.
Our constant struggle has always been how to reflect the real game as best as possible without drastically changing the landscape of the league during one offseason. Recently there has been a trend toward an arms race. Pitchers were going ridiculously early in drafts and trades were featuring first- and second-round draft picks for non-keeper-eligible starting pitchers. Our solution to reduce the value of starting pitching in our league was to move from strikeouts to K/9 so as to reflect our six stat categories: Wins, K/9, ERA, WHIP, Net Saves, and Quality Starts.
Enough about our incredibly awesome keeper league. With all the talk of the winter meetings, the World Baseball Classic, and a new year, the jump on pitching is long overdue. So, the top 155 pitchers were ranked accordingly.
Method
Steamer has released their 2017 projections. These projections, of some 4000-plus pitchers, were exported to Microsoft Excel. Pitchers were then sorted by WAR: highest to lowest. The top 155 pitchers were then selected. In a 10-team standard league, no team should roster more than 15 pitchers, giving justification for cutting off the sample at 155. Five stat categories were then selected. Steamer does not project quality starts or blown saves. Therefore, to balance the importance of SP vs RP, innings pitched was selected in addition to Wins, K/9, ERA, and WHIP.
A table was then created with the stat categories on the x-axis and the pitching running down the y-axis (if you will). Each pitcher was given a positional value based on where that pitcher ranked within each stat category. For example, Max Scherzer is projected to have an outstanding 10.93 K/9 rate, which ranks sixth in the top 155. Scherzer was therefore given a value of 6 for the K/9 category. Scores were summed for each pitcher. Pitchers were than ranked by final score. Finally, a correlation using the summed scores and pitcher rank was executed to examine the relationship between stat categories and pitcher ranks.
| Table 1: Example of Pitching Scores | |||||||
| Wins | K/9 | ERA | Whip | IP | Total | ||
| 10 | Rich Hill | 6 | 10 | 8 | 12 | 98 | 134 |
| 11 | Lance McCullers | 3 | 11 | 18 | 67 | 31 | 130 |
| 12 | Robbie Ray | 5 | 12 | 19 | 39 | 61 | 136 |
| 13 | Tyler Glasnow | 7 | 13 | 52 | 130 | 91 | 293 |
Results
A complete list of the top 155 pitchers can be found at the end of this document. Below is a list of the top 20. Of note are Lance McCullers and Robbie Ray, who rank at 17 and 19, respectively. Not surprisingly, Clayton Kershaw is number one.
| Table 2: Pitcher Rank | |
| Rank | Pitcher |
| 1 | Clayton Kershaw |
| 2 | Max Scherzer |
| 3 | Noah Syndergaard |
| 4 | Corey Kluber |
| 5 | Chris Sale |
| 6 | Madison Bumgarner |
| 7 | Jon Lester |
| 8 | Chris Archer |
| 9 | David Price |
| 10 | Stephen Strasburg |
| 11 | Carlos Carrasco |
| 12 | Yu Darvish |
| 13 | Justin Verlander |
| 14 | Jake Arrieta |
| 15 | Johnny Cueto |
| 16 | Jacob deGrom |
| 17 | Lance McCullers |
| 18 | Rich Hill |
| 19 | Robbie Ray |
| 20 | Michael Pineda |
A correlation was then performed to explore the relationships of stat categories on pitcher total scores. Table 3 highlights K/9, ERA and WHIP as very strong correlations, with ERA being the strongest. Innings pitched had the weakest correlation.
| Table 3: Correlation of Stat Categories and Total Scores | ||||||
| Wins | K/9 | ERA | WHIP | IP | Total | |
| Wins | 1 | |||||
| K/9 | 0.122264 | 1 | ||||
| ERA | 0.333911 | 0.716097 | 1 | |||
| WHIP | 0.372086 | 0.589884 | 0.815055 | 1 | ||
| IP | 0.909963 | -0.04049 | 0.138322 | 0.2326 | 1 | |
| Total | 0.594921 | 0.752427 | 0.891181 | 0.881576 | 0.458243 | 1 |
Discussion
The goal of this exercise was to explore the impact on the changing landscape of pitching stat categories in fantasy baseball. The top 20 pitchers remain starters. However, within the top 20, one can see the impact of the change to K/9 from strikeouts. Both McCullers and Ray rank inside the top-15 projected K/9, according to Steamer. This led to the question, just how much of an impact will K/9 have on total scores?
The correlation revealed a strong relationship, but not the strongest. Therefore, the answer is, it has a strong impact, but in the end not as much as ERA and WHIP. What does strong mean? Statisticians usually agree that a correlation above .75 is considered a very strong relationship. To explore this meaning, let us take a look at an extremely early positional ranking done by ESPN.
Below, we’ll play the guessing game.
| Table 4: Player Comparison | |||||
| IP | W | K | ERA | WHIP | |
| Player 1 | 174.1 | 8 | 218 | 4.90 | 1.47 |
| Player 2 | 175.1 | 7 | 167 | 4.88 | 1.27 |
The above numbers appear somewhat similar. In a standard league, you may be inclined to lean toward Player 2. Indeed, according to ESPN, Player 2 is ranked 38th at his position and Player 1 is ranked 62nd. However, when scored using the methodology in this study, Player 2 ranks 49th while Player 1 ranks 19th. Two things when considering this. Table 4 are stats from 2016. The aforementioned rankings are based on 2017 projections. It could be that Player 1 has more room to grow. However, the change from strikeouts to K/9 is evident. Player 1 (10.11) has a much better K/9 than Player 2 (8.35). Therefore, the K/9 relationship to player ranking is correctly strong, and ranking Player 1 higher than Player 2 is logical. If you were wondering, Player 1 is Robbie Ray, and Player 2 is Drew Smyly.
Limitations
Steamer does not project quality starts or blown saves, therefore the correlation could be skewed toward starters or relievers. These results should only be taken into consideration when these five stat categories are in play. The sample size of starting pitchers is large enough, but not for relief pitchers. Only five relievers were projected in the top 155 pitchers ranked by WAR. Results of the correlation, then, could look different had more relievers been incorporated.
Future research
Future research should then include additional relievers. Expanding the pitcher rankings to the top 300 would include most relevant pitchers according to Steamer. Furthermore, additional stat categories should be explored. Would adding saves and quality starts affect the rankings? Certainly, the more variables added, the more complicated the results become. However, finding a balance between starters and relievers, reflective of the real game, should be further explored.
Conclusion
A great importance is placed on starting pitching, both in the real and fake game. However, relievers seem to have a growing importance. In 2016, three months of Chapman cost the Cubs two of the game’s best prospects, a trade usually reserved for starting pitching. How to value starting pitching compared to relief pitching is left open to interpretation, especially in the world of fantasy. A reduction on starting pitching value was in order for our league and for standard leagues. How to go about this should reflect the real game. For 10 managers, the decision was to move from strikeouts to K/9.
This initial research demonstrates that this change does not swing the pendulum too far toward relievers and away from starting pitching. A correlation demonstrates the strongest relationship to pitcher ranking is ERA. Given a head-to-head matchup, with an innings limit, having multiple starters with a good ERA will still be favorable to deploying strong relievers. The top 155 pitcher rankings further confirm this fact. Initial conclusion is that a move to K/9 is a positive switch that reflects the growing importance of a good reliever, while still favoring starting pitching.
Appendix A
Top 155 Pitchers
| Name | |
| 1 | Clayton Kershaw |
| 2 | Max Scherzer |
| 3 | Noah Syndergaard |
| 4 | Corey Kluber |
| 5 | Chris Sale |
| 6 | Madison Bumgarner |
| 7 | Jon Lester |
| 8 | Chris Archer |
| 9 | David Price |
| 10 | Stephen Strasburg |
| 11 | Carlos Carrasco |
| 12 | Yu Darvish |
| 13 | Justin Verlander |
| 14 | Jake Arrieta |
| 15 | Johnny Cueto |
| 16 | Jacob deGrom |
| 17 | Lance McCullers |
| 18 | Rich Hill |
| 19 | Robbie Ray |
| 20 | Michael Pineda |
| 21 | Danny Duffy |
| 22 | Steven Matz |
| 23 | James Paxton |
| 24 | Danny Salazar |
| 25 | Carlos Martinez |
| 26 | Gerrit Cole |
| 27 | Andrew Miller |
| 28 | Aroldis Chapman |
| 29 | Kenley Jansen |
| 30 | Dellin Betances |
| 31 | Zack Greinke |
| 32 | Aaron Nola |
| 33 | Jose Quintana |
| 34 | Jameson Taillon |
| 35 | Matt Shoemaker |
| 36 | Kyle Hendricks |
| 37 | Edwin Diaz |
| 38 | Dallas Keuchel |
| 39 | Cole Hamels |
| 40 | Zach Britton |
| 41 | Masahiro Tanaka |
| 42 | Kenta Maeda |
| 43 | Jeff Samardzija |
| 44 | Tyler Skaggs |
| 45 | John Lackey |
| 46 | Vince Velasquez |
| 47 | Julio Urias |
| 48 | Matt Moore |
| 49 | Drew Smyly |
| 50 | Julio Teheran |
| 51 | Jon Gray |
| 52 | Matt Harvey |
| 53 | Kevin Gausman |
| 54 | Garrett Richards |
| 55 | Rick Porcello |
| 56 | Gio Gonzalez |
| 57 | Alex Reyes |
| 58 | Alex Wood |
| 59 | Wei-Yin Chen |
| 60 | Zack Wheeler |
| 61 | Collin McHugh |
| 62 | Carlos Rodon |
| 63 | Drew Pomeranz |
| 64 | Felix Hernandez |
| 65 | Tyson Ross |
| 66 | Matt Andriese |
| 67 | Jerad Eickhoff |
| 68 | Sean Manaea |
| 69 | Anthony DeSclafani |
| 70 | Michael Fulmer |
| 71 | Marcus Stroman |
| 72 | Blake Snell |
| 73 | Taijuan Walker |
| 74 | Tyler Glasnow |
| 75 | Ian Kennedy |
| 76 | Adam Wainwright |
| 77 | Jake Odorizzi |
| 78 | Jaime Garcia |
| 79 | Yordano Ventura |
| 80 | Joe Ross |
| 81 | J.A. Happ |
| 82 | Aaron Sanchez |
| 83 | Sonny Gray |
| 84 | Jharel Cotton |
| 85 | Hisashi Iwakuma |
| 86 | Michael Wacha |
| 87 | Francisco Liriano |
| 88 | Drew Hutchison |
| 89 | Mike Foltynewicz |
| 90 | Lance Lynn |
| 91 | Ricky Nolasco |
| 92 | Jeremy Hellickson |
| 93 | Archie Bradley |
| 94 | Luis Severino |
| 95 | Nate Karns |
| 96 | Mike Leake |
| 97 | Bartolo Colon |
| 98 | Mike Montgomery |
| 99 | Tyler Anderson |
| 100 | Ervin Santana |
| 101 | Junior Guerra |
| 102 | Ivan Nova |
| 103 | Chad Green |
| 104 | Tanner Roark |
| 105 | Jason Hammel |
| 106 | Mike Fiers |
| 107 | Dan Straily |
| 108 | R.A. Dickey |
| 109 | Doug Fister |
| 110 | Marco Estrada |
| 111 | Homer Bailey |
| 112 | Jesse Chavez |
| 113 | Ty Blach |
| 114 | Jordan Zimmermann |
| 115 | Trevor Bauer |
| 116 | Brandon Finnegan |
| 117 | Edinson Volquez |
| 118 | Charlie Morton |
| 119 | Daniel Norris |
| 120 | Cesar Vargas |
| 121 | Zach Davies |
| 122 | Adam Conley |
| 123 | Eduardo Rodriguez |
| 124 | Derek Holland |
| 125 | Luis Perdomo |
| 126 | Alex Cobb |
| 127 | Jose Berrios |
| 128 | Josh Tomlin |
| 129 | Shelby Miller |
| 130 | Chad Bettis |
| 131 | Patrick Corbin |
| 132 | CC Sabathia |
| 133 | Christian Friedrich |
| 134 | Hector Santiago |
| 135 | Kendall Graveman |
| 136 | Anibal Sanchez |
| 137 | Steven Brault |
| 138 | Tyler Chatwood |
| 139 | Wade Miley |
| 140 | Chris Tillman |
| 141 | Dylan Bundy |
| 142 | Andrew Triggs |
| 143 | Jason Vargas |
| 144 | Matt Garza |
| 145 | Phil Hughes |
| 146 | Miguel Gonzalez |
| 147 | Kyle Gibson |
| 148 | Ariel Miranda |
| 149 | Tom Koehler |
| 150 | Jorge de la Rosa |
| 151 | Chase Anderson |
| 152 | Martin Perez |
| 153 | Chad Kuhl |
| 154 | Andrew Cashner |
| 155 | Wily Peralta |





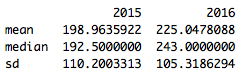
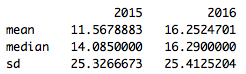
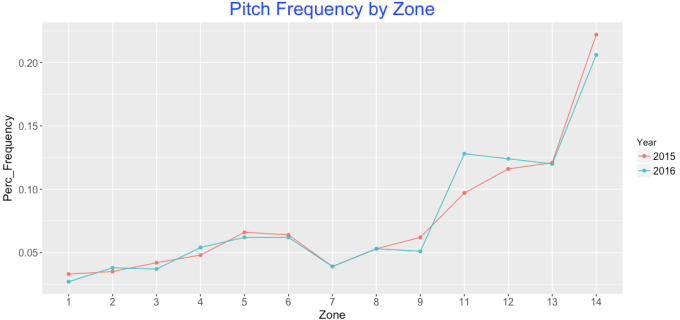
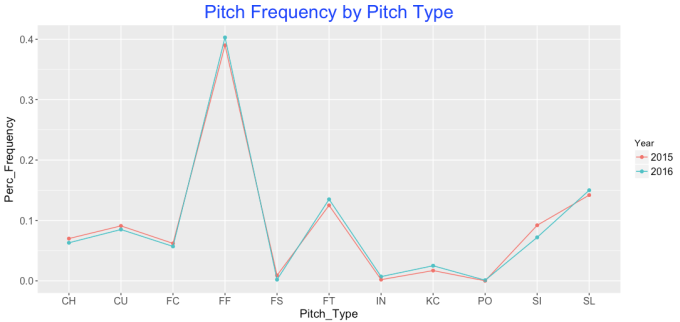





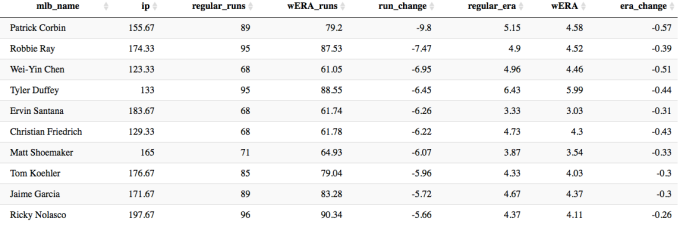
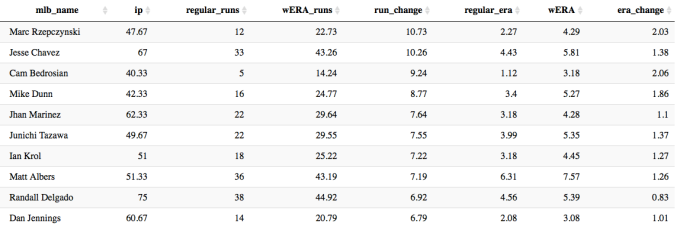
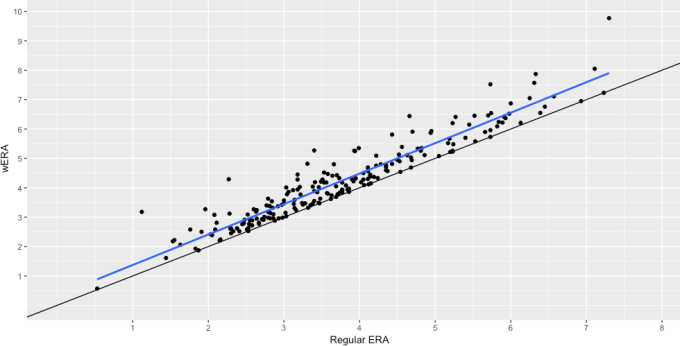
 Let’s take a look at the 2016 season, and see which starting and relief pitchers would be least and most affected by this version of the ERA calculation (note: only showing starters with at least 100 IP, and relievers with over 30 IP).
Let’s take a look at the 2016 season, and see which starting and relief pitchers would be least and most affected by this version of the ERA calculation (note: only showing starters with at least 100 IP, and relievers with over 30 IP).