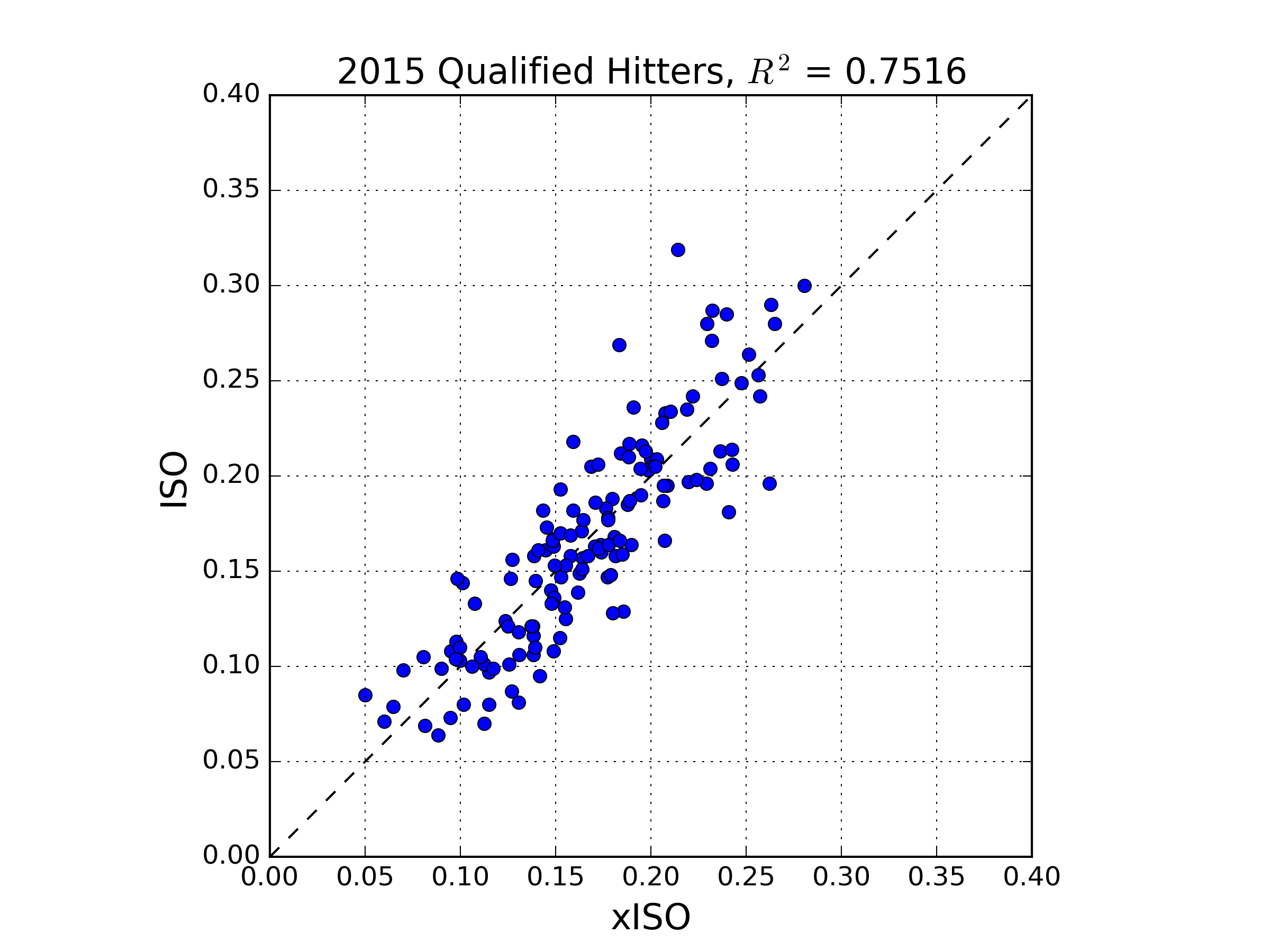
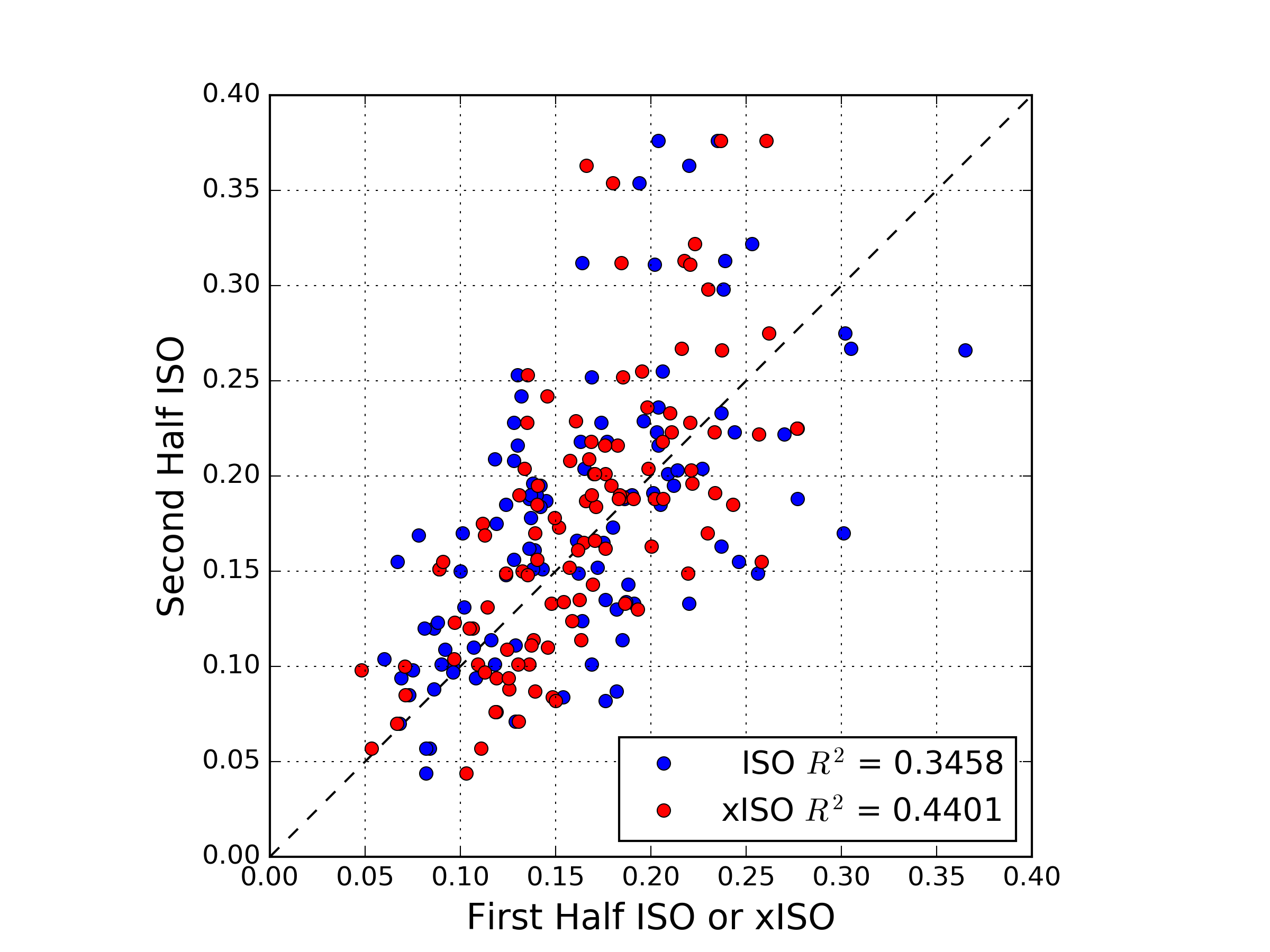
Kinda Juiced Ball: Nonlinear COR, Homers, and Exit Velocity
At this point, there’s very little chance you are both (a) reading the FanGraphs Community blog and (b) unaware that home runs were up in MLB this year. In fact, they were way up. There are plenty of references out there, so I won’t belabor the point.
I was first made aware of this phenomenon through a piece written by Rob Arthur and Ben Lindbergh on FiveThirtyEight, which noted the spike in homers in late 2015 [1]. One theory suggested by Lindbergh and Arthur is that the ball has been “juiced” — that is, altered to have a higher coefficient of restitution. Since then, one of the more interesting pieces I have read on the subject was written by Alan Nathan at The Hardball Times [2]. In his addendum, Nathan buckets the batted balls into discrete ranges of launch angle, and shows that the mean exit speed for the most direct contact at line-drive launch angles did not increase much between first-half 2015 and first-half 2016. He did observe, however, that negative and high positive launch angles showed a larger increase in mean exit speed. Nathan suggests that this is evidence against the theory that the baseball is juiced, as one would expect higher mean exit speed across all launch angles. I have gathered the data from the excellent Baseball Savant and reproduced Nathan’s plot for completeness, also adding confidence intervals of the mean for each launch angle bucket.
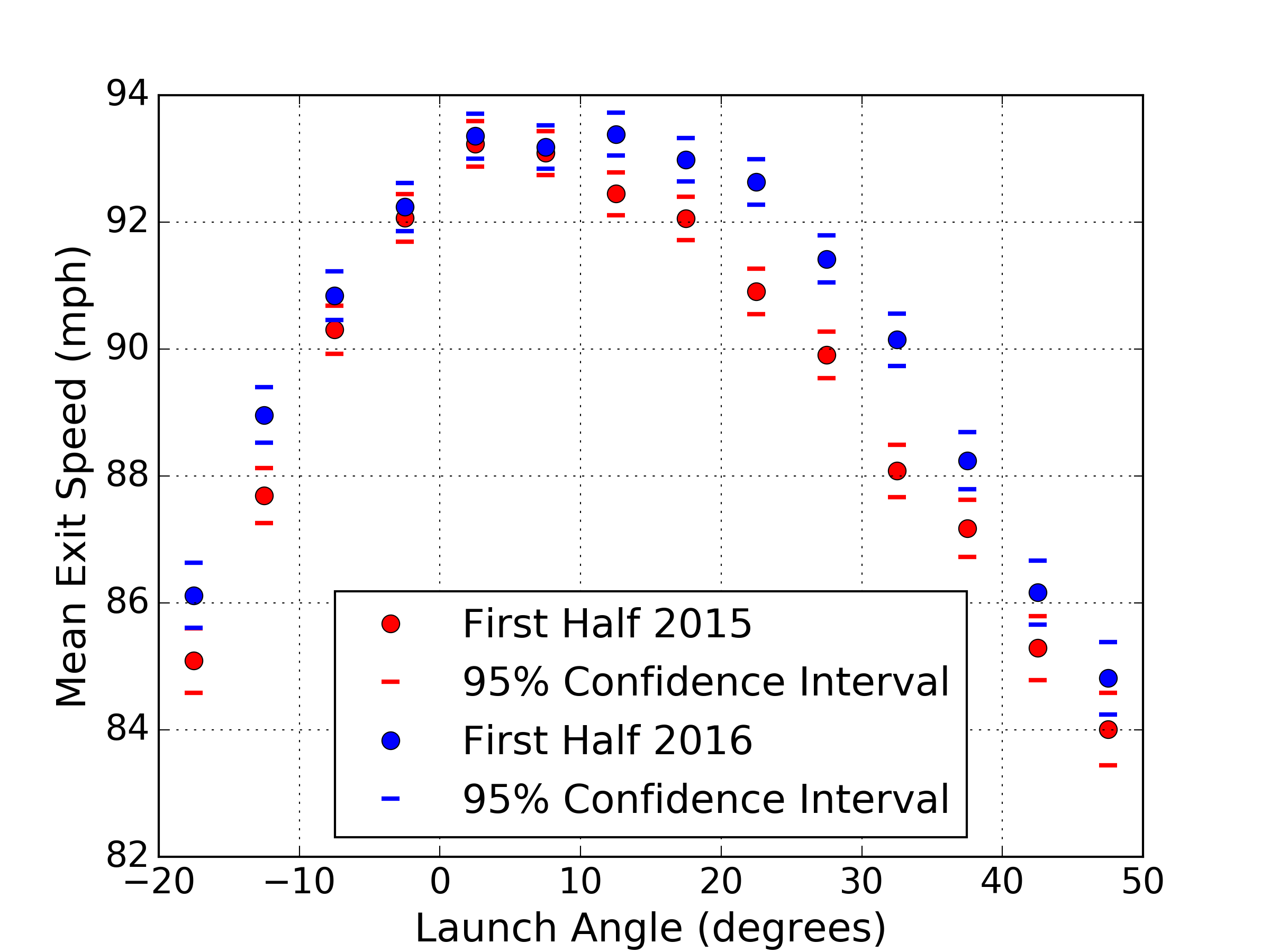
Figure 1. Mean exit speed vs. launch angle.
At the time of this writing, I am not aware of any concrete evidence to support the conclusion that the baseball has been intentionally altered to increase exit speed. This fact, combined with Nathan’s somewhat paradoxical findings, led me to consider a subtler hypothesis: some aspect of manufacturing has changed and slightly altered the nonlinear elastic characteristics of the ball. Now, I’ve been intentionally vague in the preceding sentence; let me explain what I really mean.
Coefficient of restitution (COR) is a quantity that describes the ratio of relative speed of the bat and ball after collision to that before collision. The COR is a function of both the bat and the ball, where a value of 1 indicates a perfectly elastic collision, during which the total kinetic energy of the bat and ball in conserved. The simplest, linear, approximation of COR is a constant value, independent of the relative speed of the impacting bodies. It has long been known that, for baseballs, COR takes on a non-linear form, where the value is a function of relative speed [3]. Specifically, the COR decreases with increasing relative speed, and can vary on the order of 10% across a typical impact speed range. My aim is to show that, for some reasonable change in the non-linear COR characteristics of the baseball, I can reproduce findings like Alan Nathan’s, and offer yet another theory for MLB’s home-run spike.
In order to explore this, I first need a collision model to incorporate a non-linear COR. I want this model to be relatively simple, and also to be able to account for different impact angles between bat and ball. This is what will allow me to explore the effect of non-linear COR on exit speed vs. launch angle. I will mostly follow the work of Alan Nathan [4] and David Kagan [5]. I won’t show my derivation; rather, I will include final equations and a hastily drawn figure to explain the terms.

Figure 2. Hastily drawn batted-ball collision.
The ball with mass m is traveling toward the bat with speed , assumed exactly parallel to the ground for simplicity. The bat with effective mass M is traveling toward the ball with speed
, at an angle
from horizontal. We know that in this two-dimensional model, the collision occurs along contact vector, the line between the centers of mass, which is at an angle
from horizontal. This will also be the launch angle. Intuition, and indeed physics, tells us that the most energy will be transferred to the ball when the bat velocity vector is collinear with the contact vector. When the bat is traveling horizontally and the ball impacts more obliquely, above the center of mass of the bat, the ball will exit at a lower speed. These heuristics are captured with the following equations, where COR as a function of relative speed will be denoted
, and the exit speed
.
(1)
(2)
(3)
(4)
(5)
Now all we must do is choose a functional dependence of the COR on relative speed. Following generally the data from Hendee, Greenwald, and Crisco [3], and making small modifications, I produced the following models of COR velocity dependence:

Figure 3. Hypothetical non-linear COR.
Note that, for the highest relative bat/ball collisions, the “old” and “new” ball/bat collisions will result in similar amounts of energy transferred, while in the “new” ball model, slightly more energy will be transferred to the ball in lower-speed collisions. This difference seems to me quite plausible given manufacturing and material variation of the baseball. It is also worth emphasizing that this difference need only be on average for the whole league; some variation ball-to-ball would be expected.
Taking the new and old ball COR models from Figure 3 and plugging into equations (1)-(5) allows us to simulate the exit speed across a range of launch angles. I have assumed a bat swing angle of 9 degrees. Calculations and plots are accomplished with Python.

Figure 4. Exit speed as a function of launch angle for non-linear COR.
The first thing to note about Figure 4 is that the highest exit speed is indeed at 9 degrees, which was the assumed bat path. The second is the remarkable likeness between Figure 4, the model, and Figure 3, the data. Clearly, I have cheated by tweaking my COR models to qualitatively match the data, but the point is that I did not have to make wildly unrealistic assumptions to do so. I have not looked deeply into the matter, but this hypothesis would also suggest that from ’15 to ’16, a larger home-run increase would be expected for moderate power hitters than from those who hit the ball the very hardest. In fact, Jeff Sullivan suggests almost exactly this [6], although he also produces evidence somewhat to the contrary [7].
There is certainly much complexity that I am ignoring in this simple model, but it is based on solid fundamentals. If one accepts that baseball manufacturing could be subject to small variations, and perhaps a small systematic shift that alters the non-linear coefficient of restitution of the ball, it follows that the exit speed of the baseball is also expected to change. Further, the exit speed is expected to change differently as a function of launch angle. That a simple model of this phenomenon can easily be constructed to match the actual data from suspected “before” and “after” timeframes is at least interesting circumstantial evidence for the baseball being juiced. Perhaps not exactly the way we all expected, but still kinda juiced.
References:
[1] Arthur, Rob and Lindbergh, Ben. “A Baseball Mystery: The Home Run Is Back, And No One Knows Why.” FiveThirtyEight. 31 Mar. 2016. Web. 30 Aug. 2016.
[2] Nathan, Alan, “Exit Speed and Home Runs.” The Hardball Times. 18 Jul. 2016. Web. 23 Aug. 2016.
[3] Hendee, Shonn P., Greenwald, Richard M., and Crisco, Joseph J. “Static and dynamic properties of various baseballs.” Journal of Applied Biomechanics 14 (1998): 390-400.
[4] Nathan, Alan M. “Characterizing the performance of baseball bats.” American Journal of Physics 71.2 (2003): 134-143.
[5] Kagan, David. “The Physics of Hard-Hit Balls.” The Hardball Times. 18 Aug. 2016. Web. 23 Aug 2016.
[6] Sullivan, Jeff. “The Other Weird Thing About the Home Run Surge.” FanGraphs. 28 Sept. 2016. Web. 4 Dec. 2016.
[7] Sullivan, Jeff. “Home Runs and the Middle Class.” FanGraphs. 28 Sept. 2016. Web. 4 Dec. 2016.