Progressive Pitch Projections: Four-Seam Fastballs (+ PITCHf/x Simulation)
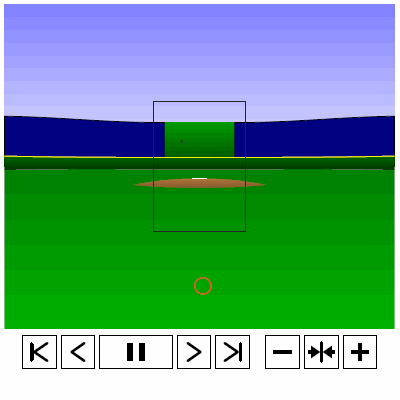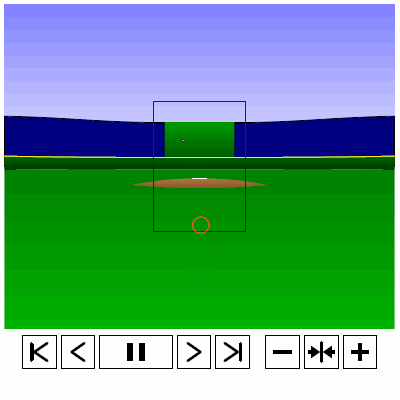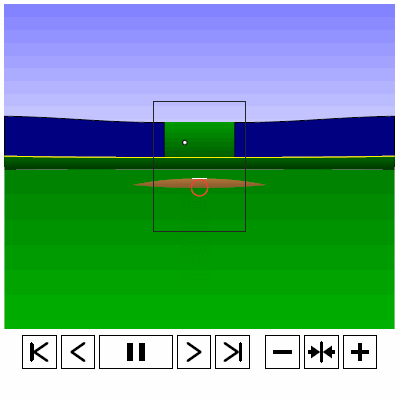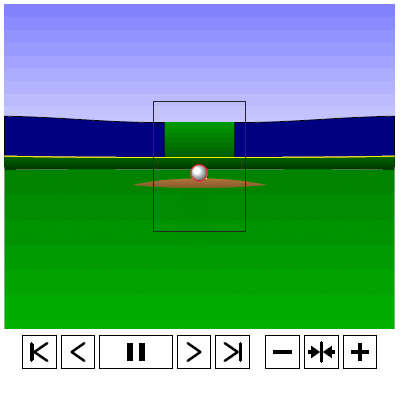
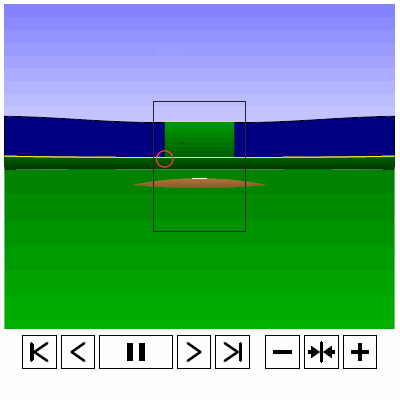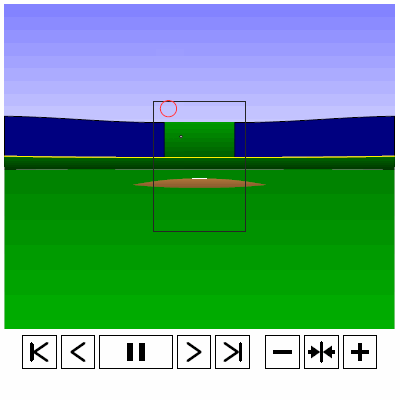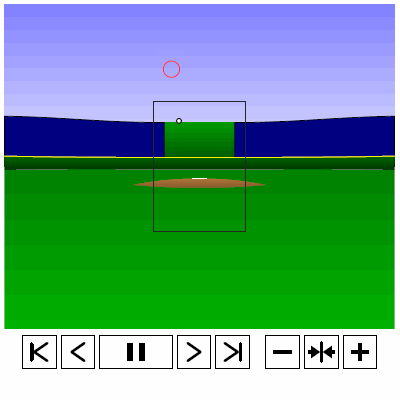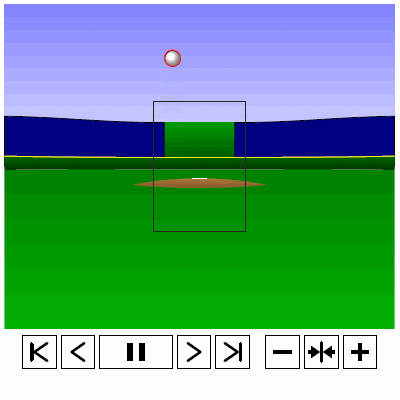
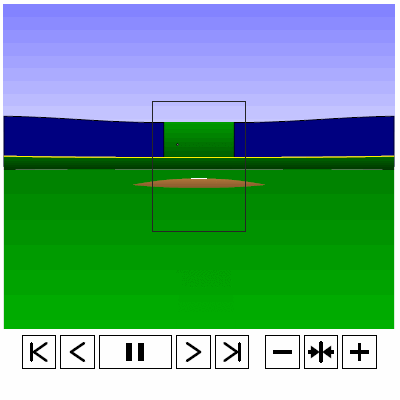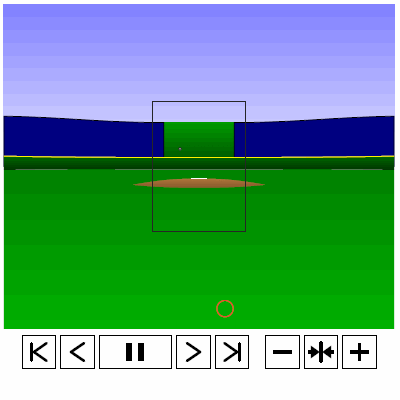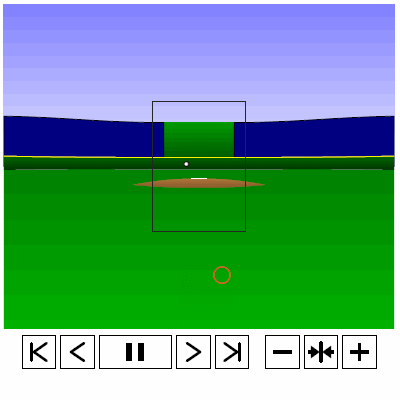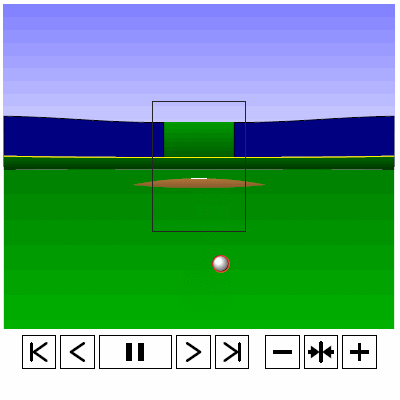
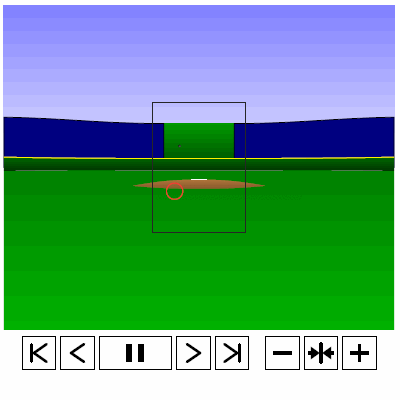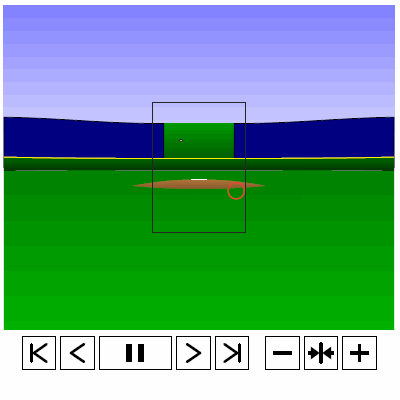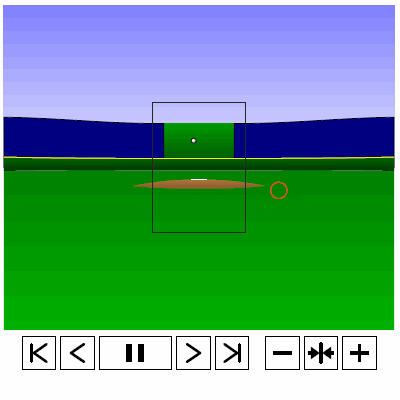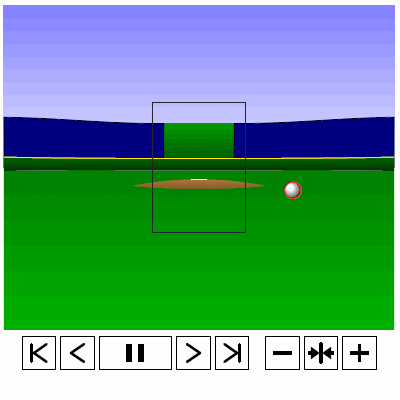
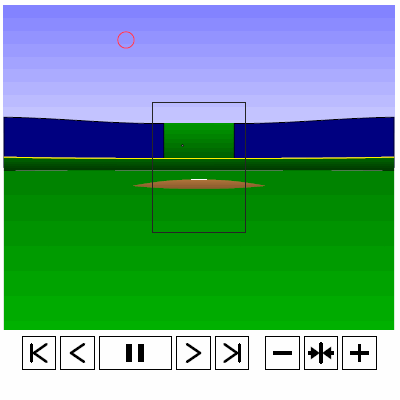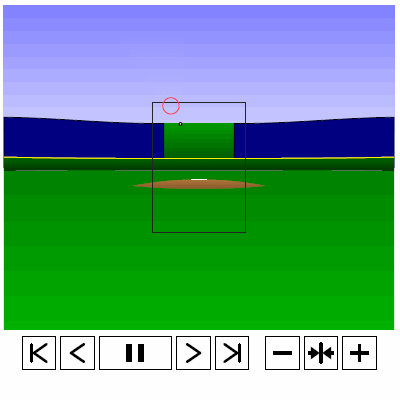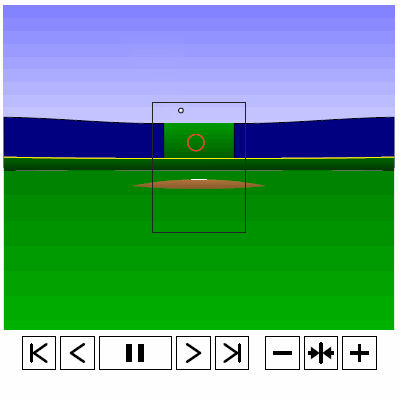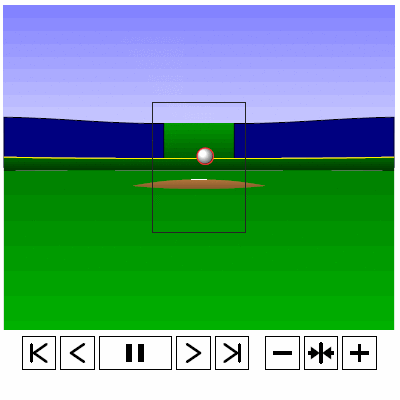
Last time, we analyzed Yu Darvish’s sliders in terms of when they projected as strikes and how pitch movement affected perception, leading batters to swing at pitches outside of the strike zone in the direction of the pitch movement. This time, we will turn our focus to four-seam fastballs. As before, we are using the 2013 data set since the algorithms for this were run before the completion of the 2014 season. To start, we can examine a four-seam fastball from Yu Darvish, his second-most thrown type of pitch in 2013, via simulation using the nine-parameter PITCHf/x data for its trajectory. The chosen fastball from Darvish was thrown roughly down the middle of the strike zone and we also track the projection of the pitch as it approaches the plate.
Note that the pitch, in this case, is simulated at one-quarter actual speed. The strike zone shown is the standard width of the plate and 1.5 to 3.5 feet vertically. The red circle represents the projection of the pitch after removing the remaining PITCHf/x definition of movement from its current location (Note that while the simulation shown above is a GIF, the actual simulation is an interactive PDF where the controls at the bottom of the image can play, rewind, slow down, etc. the simulation. This is discussed at the end of the article for the interested reader, including a link to several interactive PDFs as well as a tutorial for the controls and the source code written in TeX). Here, the movement causes the pitch to rise, giving the pitch in the simulation a “floating” quality as it never seems to drop.
As in the previous work on sliders, we will start by splitting the four-seamers into four groups based on the pitch location and the batter’s response: strikes (pitches with a 50% chance or better of being called a strike) and balls (lower than 50% chance of being called a strike), and swings and pitches taken. Working with the projections to the front of the plate after removing the remaining movement on the pitch, we can examine how attractive (in terms of probability that the projection will be called a strike) pitches in each of these four categories, on average, are to batters incrementally as they approach the plate.
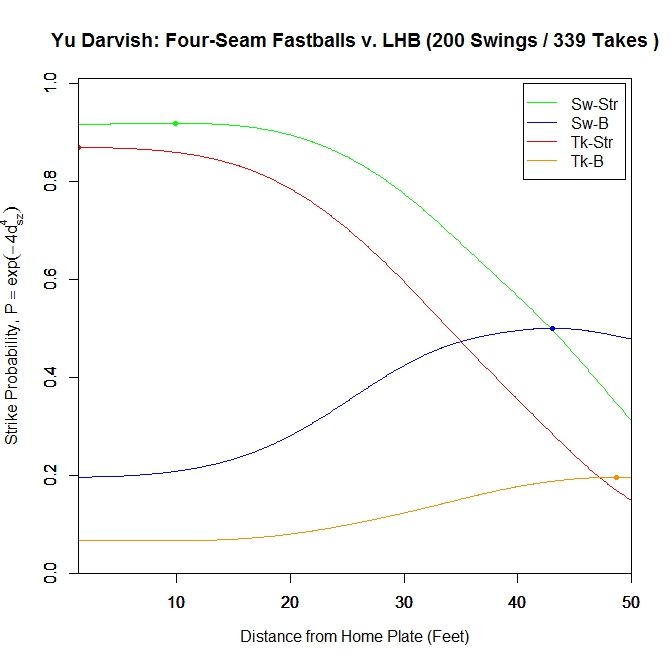
To begin, for left-handed batters versus Darvish in 2013:
For both types of pitches in the strike zone (red=taken, green=swung at), the average probability of the pitch being called a strike levels off around 20 feet, with strikes swung at peaking at probability 0.919 at 9.917 feet from home plate, then dropping to 0.917 at the plate. Strikes taken reach their maximum at the front of the plate with probability 0.869. The four-seamers swung at outside of the strike zone (blue) average around 0.5 probability of being called a strike up until around 30 feet, before dropping off. The fastballs taken outside the zone (orange) tend to project as low-probability strikes initially and remain so to the front of the plate.
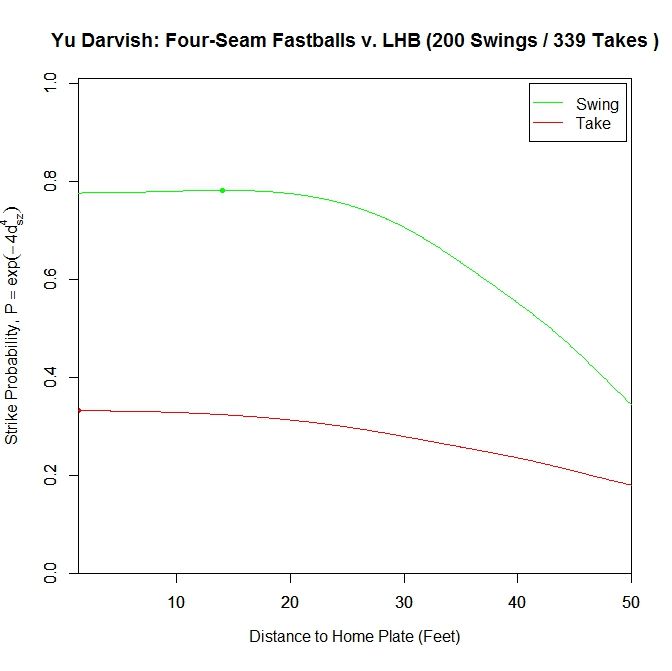
We can simplify this graph to include only swings and pitches taken.
Once again, pitches swung at project as better pitches throughout than those taken. The peak for swings is at 14.083 feet with probability 0.782, and finishes at 0.777. The pitches taken keep increasing in attractiveness all the way to the front of the plate, reaching a called-strike probability of 0.332.
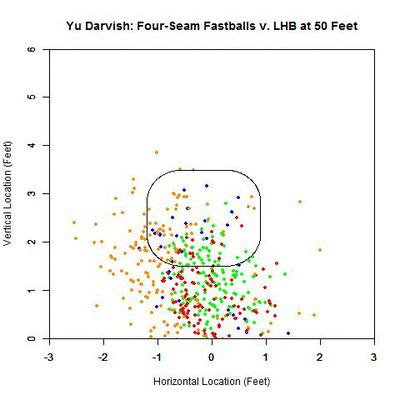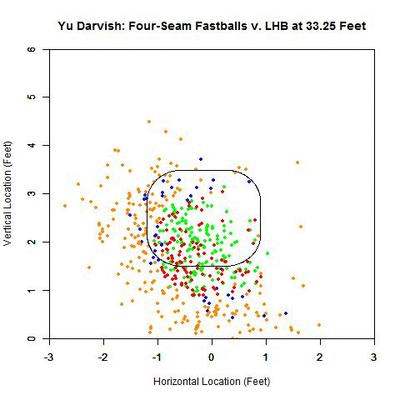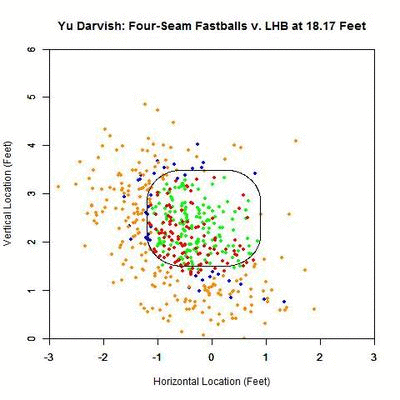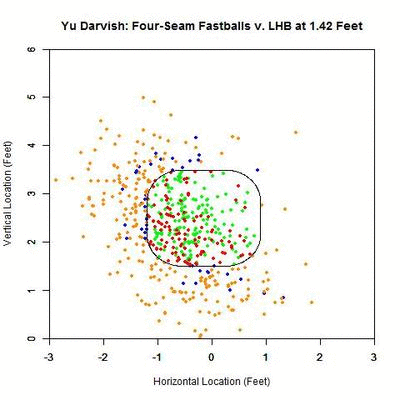
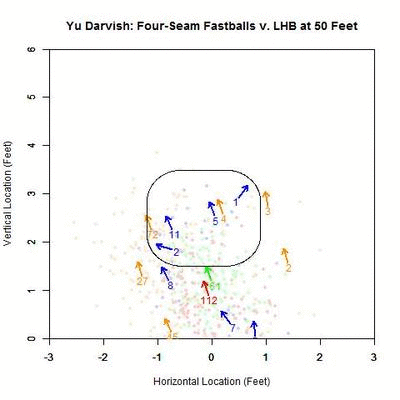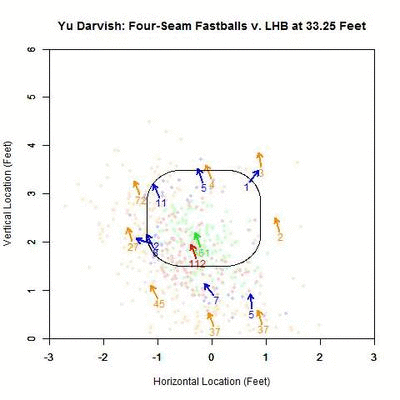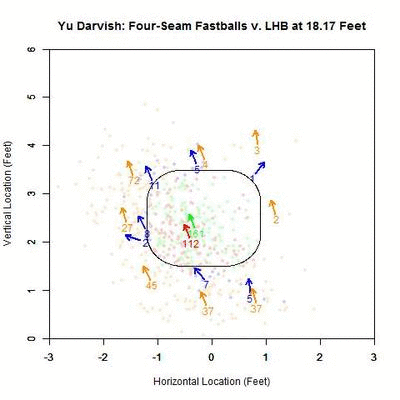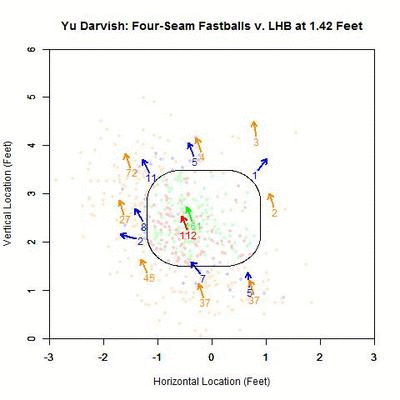
To further examine what is happening in these graphs, we can view the location of these projections from 50 feet to the front of home plate. The color scheme is the same as the four-curve plot above.
Focusing on the blue projections for the moment (swings outside the strike zone), the projections down and to the right of the zone are carried by movement toward the strike zone and most end up as borderline strikes. Those up and to the left project further and further outside the strike zone as they approach the plate, since their direction of movement is roughly perpendicular to the strike zone contour. To get a better idea of the number of each of the four cases in nine regions in and around the strike zone, we can fade the data into the background and replace it in each region by an arrow indicating the direction that the average projection for that area is moving and the number of pitches of that case located there.
Focusing first on the pitches in the strike zone, there is a dearth of projections in the upper-right area, which would be on the inside half of the plate to LHB. The pitches taken in the strike zone tend to skew slightly down and to the left, relative to those swung at. Note that in many of the regions around the strike zone, the samples are quite small so it may be difficult to draw any strong conclusions. With this in mind, these results can be summarized in the following table where the center cell represents the swing percentage in the strike zone and all other cells contain the percentage of swings in that region.
| Darvish – Four Seamers vs. LHB | ||
| 13.3 | 55.6 | 25 |
| 22.9 | 59 | 0 |
| 4.3 | 15.9 | 11.9 |
The region with the highest swing percentage is the strike zone, at 59%. The region with the next highest percentage is above the strike zone, which is in the general direction of movement, but here there are only nine data points to rely on for this percentage. It would seem that the regions that induce swings are those where the pitches project in the strike zone and are carried out by movement (above and above-and-left of the zone) and where the pitches project as balls but movement is carrying them toward the zone (below and below-and-right of the zone). Notice that the area below and left of the strike zone has 47 pitches thrown there and only 2 swings, which is where the movement parallels the strike zone.
It would appear, based on these observations, that the location of the pitch, relative to the direction of the movement, has an influence on generating swings outside the strike zone. As with the sliders in the previous article, we will use, as a measure of if the pitch is thrown outside in the direction of movement, the angle between the movement of the four-seam fastballs at 40 feet (the pfx_x and pfx_z variables in the PITCHf/x data set) outside the zone and a vector perpendicular to the strike zone extending to the final location of the pitch at the front of home plate. An angle of zero indicates that the movement of the pitch carried it perpendicularly away from the strike zone. Ninety degrees means that the pitch projection parallels the strike zone due to movement. A one-eighty degree angle means that the pitch is being carried by movement perpendicularly toward the strike zone. Further explanation, including a visual depiction, can be found in the link to the previous article at the top of this page.
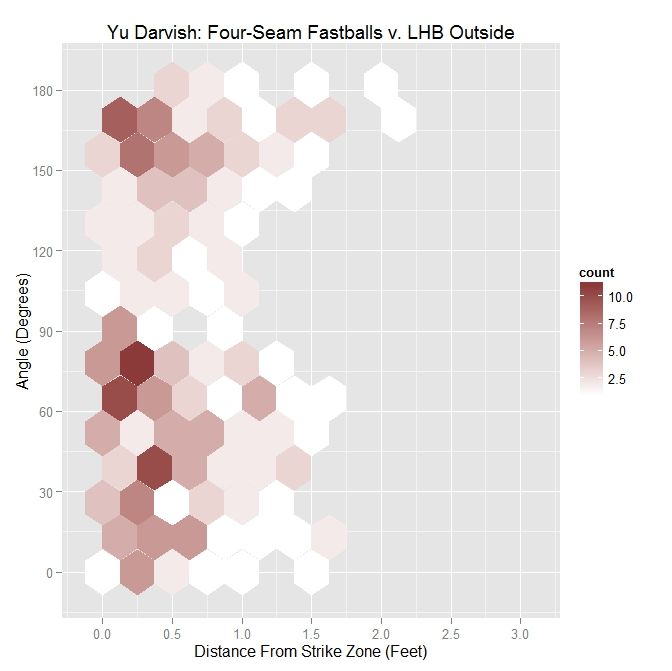
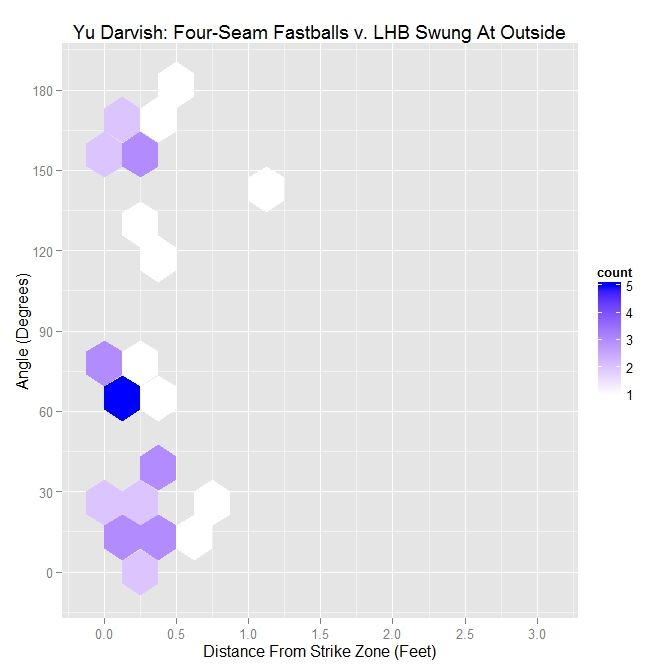
To begin, we will look at the distribution of angle versus distance from the strike zone for all of Darvish’s four-seamers outside the zone to lefties.
| Darvish – Four Seamers Outside the Zone v. LHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 28.9 | 0.546 | |||
| Less Than 90 Degrees | 58.6 | 0.517 | |||
| All | X | 0.553 | |||
The distribution, in this case, seems slightly skewed toward having pitches thrown in the general direction of movement. This visual assessment is supported by the percentages in the table (sorted by angle and average distance from the strike zone contour in feet. e.g., 0.5 = 6 inches, 0.33 = 4 inches), with nearly 29% of pitches having an angle of less than 45 degrees and over 58% with an angle less than 90 degrees. The distribution does not seem to have definitive shape.
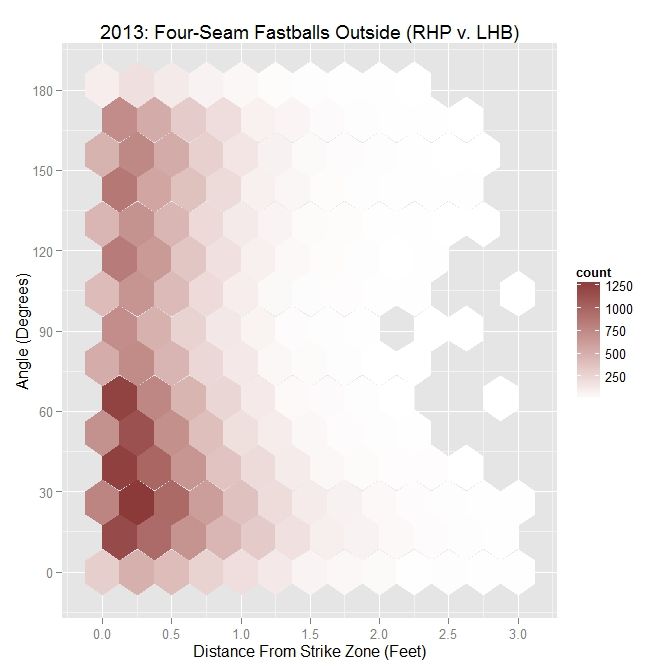
| MLB RHP 2013 – Four Seamers Outside the Zone v. LHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 37.5 | 0.557 | |||
| Less Than 90 Degrees | 61.9 | 0.501 | |||
| All | X | 0.477 | |||
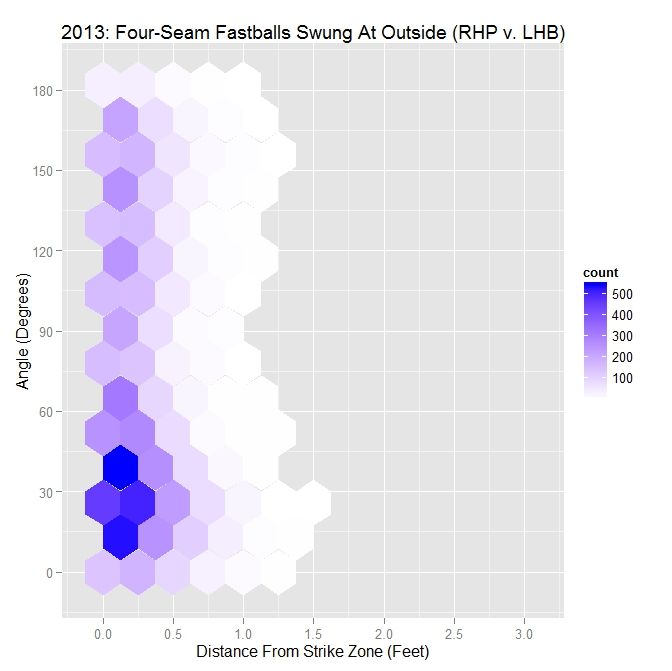
For all MLB right-handed pitchers in 2013, including Darvish, the distribution is much more clear. There is a swell of pitches thrown with angle between 0 and 90 degrees and within six inches of the strike zone, with 37.5% thrown with an angle of less than 45 degrees, and 61.9% with an acute angle. In conjunction, as the angle increases, the average distance from the strike zone decreases. To get a better handle on the ramifications of this choice of pitch locations, we can further sort the data into swings and pitches taken.
| Darvish – Four Seamers Swung At Outside the Zone v. LHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 43.6 | 0.315 | |||
| Less Than 90 Degrees | 69.2 | 0.232 | |||
| All | X | 0.248 | |||
For Darvish, nearly 44% of the pitches swung at had an angle between the vector perpendicular to the strike zone and the movement vector of less than 45 degrees. For those less than 90 degrees, this percentage jumps to nearly 70%. In addition, the average distance outside with angle less than 45% is an average of 4 inches outside whereas, overall, the average is about 3 inches in all directions. We can compare this to Darvish’s right-handed colleagues in 2013:
| MLB RHP 2013 – Four Seamers Swung At Outside the Zone v. LHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 46.9 | 0.267 | |||
| Less Than 90 Degrees | 66.8 | 0.248 | |||
| All | X | 0.238 | |||
For MLB righties, the largest area of swings is right around a 30-degree angle. Close to half of the swings, 46.9% to be exact, occur when the angle is less than 45 degree and over two-thirds are for pitches in the general direction of movement. The average distance on four-seamers swung at outside is close to Darvish’s overall, but is almost an inch further out for Darvish for 45-degree or less angles. So for RHP to LHB, pitches thrown in the neighborhood of 30 degrees and within a half-foot of the strike zone tend to induce swings, which is also seen for Darvish. We can now look at the complement of this, pitches taken outside, to see how this distribution compares to swings.
| Darvish – Four Seamers Taken Outside the Zone v. LHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 26.4 | 0.611 | |||
| Less Than 90 Degrees | 56.8 | 0.577 | |||
| All | X | 0.605 | |||
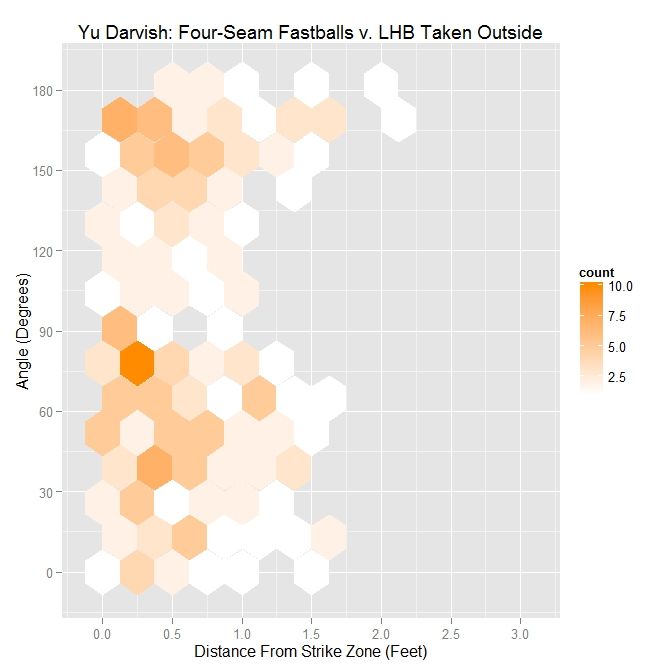
The distribution for Darvish on pitches taken has some semblance to that for all pitches, but the percentages have dropped in all cases. In addition, the average distances across the board are over six inches outside.
| MLB RHP 2013 – Four Seamers Taken Outside the Zone v. LHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 35.1 | 0.654 | |||
| Less Than 90 Degrees | 60.7 | 0.571 | |||
| All | X | 0.537 | |||
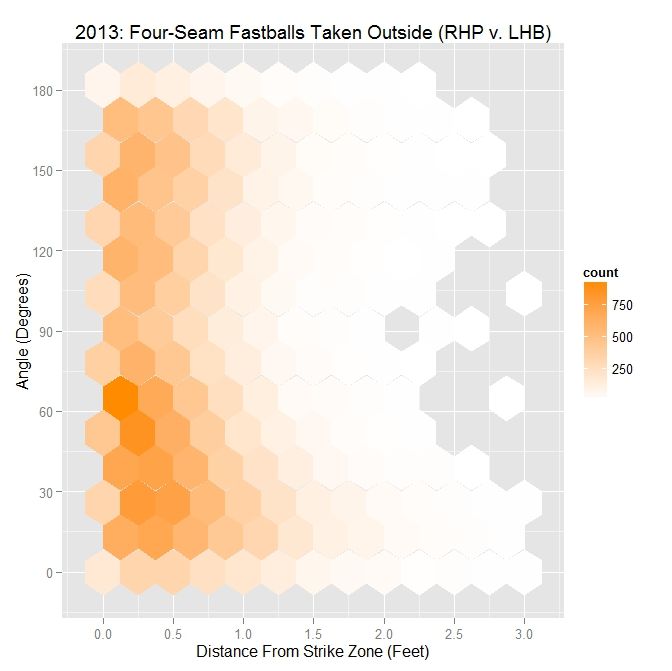
For all MLB RHP in 2013, the pitches taken by LHB outside the strike zone are largely located below 90 degrees, with a large number near 60 degrees. Compared to the case of all pitches outside the strike zone, the percentages are not all that dissimilar, but the distances are slightly larger. Putting the two hexplots together to see how they form the plot for all outside pitches, we see that what appears to be one large grouping of data below 90 degrees for all pitches separates into two smaller groupings: one around 30 degrees for swings and one around 60 degrees for pitches taken.
To examine why it might be the case that pitches thrown in the direction of movement, meaning a small angle between the movement vector and the vector perpendicular to the strike zone, are swung at more frequently and are more effective at inducing swings further from the strike zone than those that are not, we can take a four-seamer thrown by Darvish above the strike zone and examine both the trajectory of the pitch and its projection. We can again simulate such a pitch (at quarter speed) via the PITCHf/x data for Darvish. Note that since the below simulation does not possess the same computational capabilities as the rest of the code, which is done in R, we use the standard strike zone as a reference rather than the 50% contour.
Based on the simulation and associated projection, we can see that the pitch projects as a strike early on and, late in its trajectory, appears to be a ball. The important observation for this is that, for some part of its flight, the pitch does appear that it may be a strike. Similarly, for a pitch below the strike zone, we see the opposite result.
One can see the problem with getting a batter to swing at a pitch such as this. It starts out as looking like a pitch in the dirt and, through its path to the plate, only slightly improves its chances of being called a strike, and at no point really gives the batter much incentive to swing at it. Thus it makes sense that a batter might swing at a four-seam fastball high above the strike zone but not one a similar distance beneath.
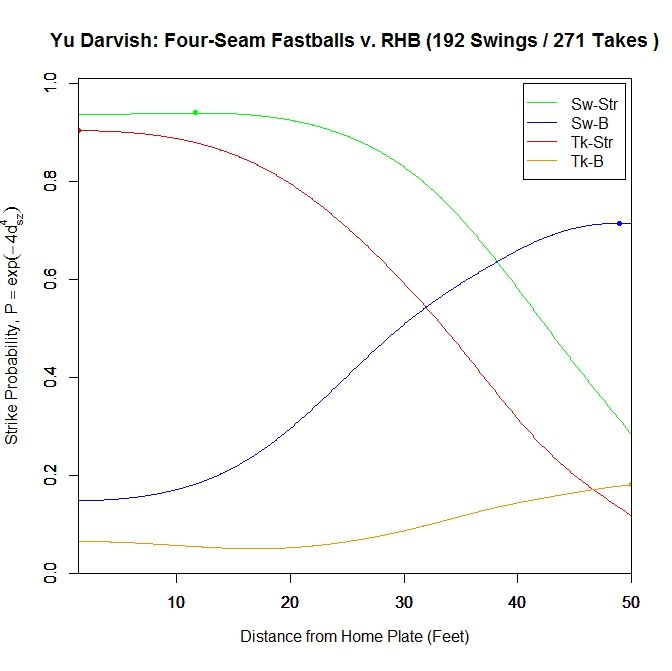
Performing the same analysis for right-handed batters, we again start with Darvish’s results for the four-seam fastball in terms of ball/strike and swing/take.
Here, the swing/strike curve peaks at probability 0.94 at 11.667 feet and finishes at 0.937. These probabilities are slightly higher than those for lefties at the maximum and at the front of the plate. The pitches taken in the strike zone peak at the plate with probability 0.904, compared to 0.869 for LHB. For both cases of pitches outside the strike zone, they reach their maximum very early in the trajectory and drop off afterward.
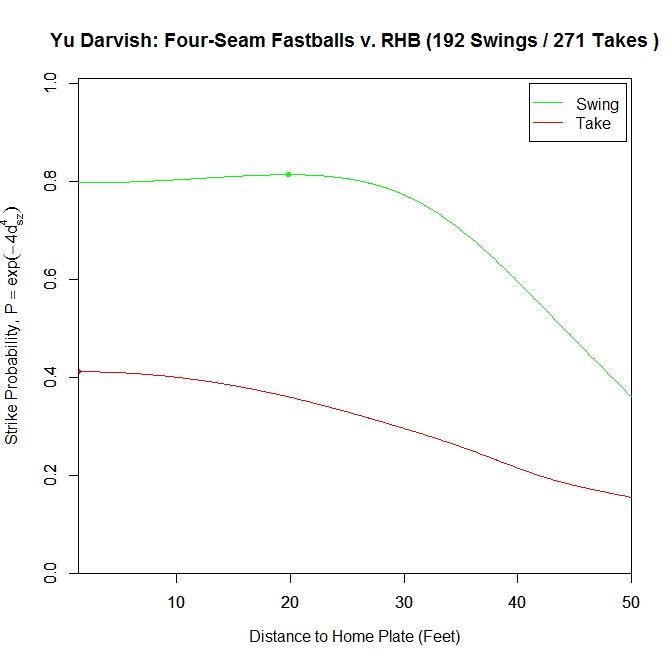
Changing to the two-curve representation for four-seam fastballs to right-handers, the swing curve reaches its apex of probability 0.814 at 19.833 feet and ends with probability 0.797 at the plate. For pitches taken, the average strike probability increases throughout the trajectory, ending at 0.411. Once again, these probabilities are higher than for left-handed batters.
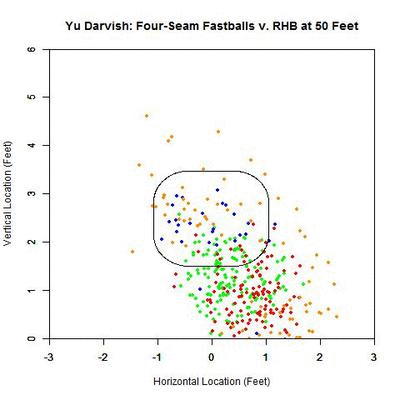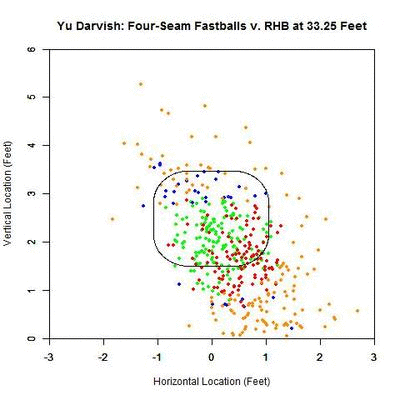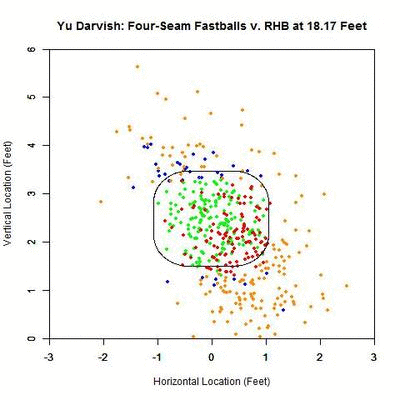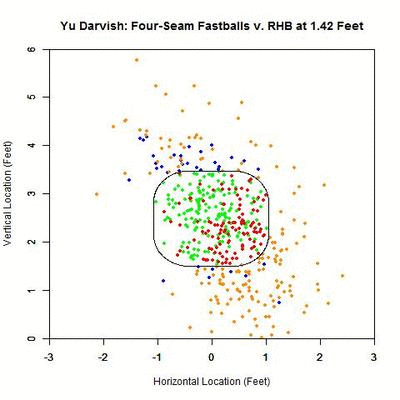
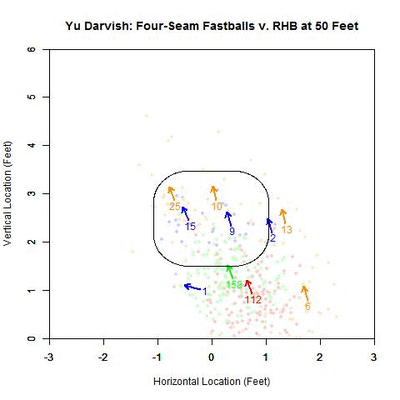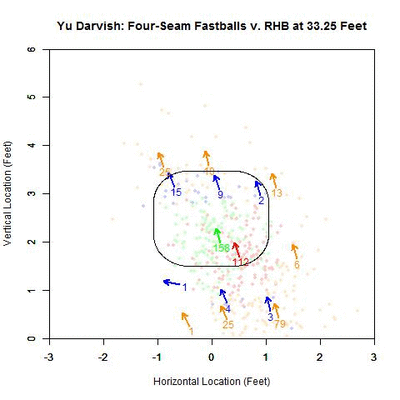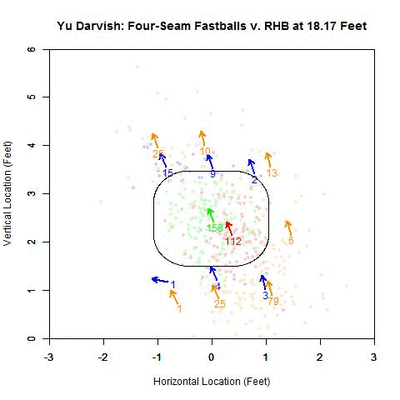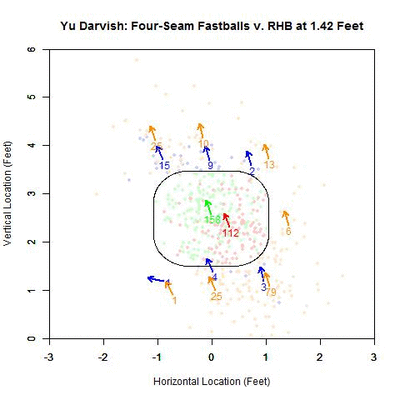
As before, we can switch to the discrete data and their projections as the pitches near the front of home plate. Of note is that the pitches taken (red data points) are, by and large, down and to the right of the strike zone from the catcher’s perspective, which is in the opposite direction that the movement influences the pitches as they approach the plate. In addition, the majority of swings outside the strike zone, the blue data points, leave the strike zone in the direction of movement. Also of interest is that the pitches fill up the strike zone more against RHB, while four-seamers to LHB were lacking for the inner half of the strike zone. For the pitches swung at outside the strike zone in the opposite the direction of movement, down and to the right, they end up very close the strike zone contour, making them boarderline strikes, and thus nominally classified outside the zone. To observe these phenomena more succinctly, we can switch to a vector representation indicating the number of pitches and the direction that the projections are headed for each of the nine regions in and around the strike zone.
Of the 270 pitches in the defined strike zone, the average location of the 112 taken were down and to the right of those swung at, as represented by the red and green arrows. To quantify the percentage of swings in each of the nine regions, we can refer to the below table, aligned spatially with the data from the GIF (center square being in the strike zone).
| Darvish – Four Seamers vs. RHB | ||
| 37.5 | 47.4 | 13.3 |
| X | 58.5 | 0 |
| 50 | 13.8 | 3.7 |
Based on these results and for regions with more than a handful of pitches, the highest percentages of swings outside the strike zone are in the upper and upper-left regions, in the direction of movement. The lower-left corner is large as well but can be disregarded as it only contains two pitches, one of which was swung at. Also, it is hard to draw any conclusions to the left of the plate since there is no data.
We can now turn our attention to pitches outside the zone for both Darvish and other MLB righties in 2013:
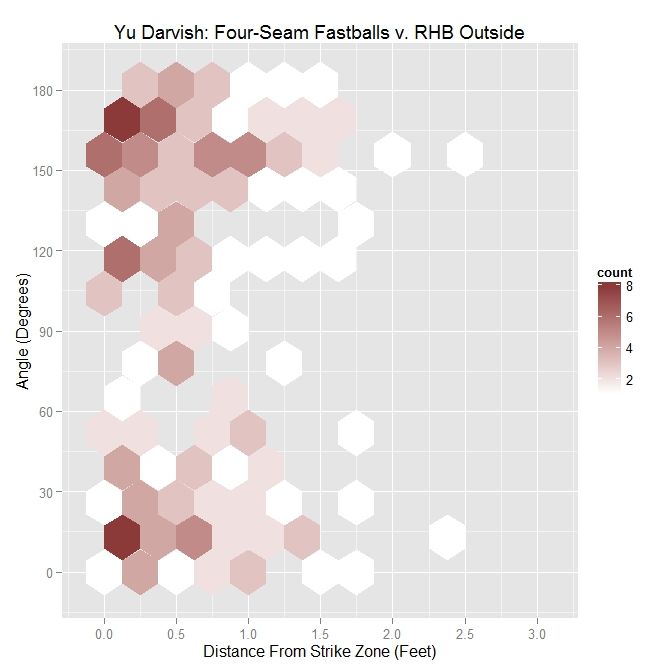
First, for Darvish, the distribution of pitches, when viewed by plotting distance from the strike zone versus angle between the perpendicular vector to the strike zone and the movement vector, appears bimodal with a large grouping both above and below the 90-degree mark.
| Darvish – Four Seamers Outside the Zone v. RHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 31.2 | 0.633 | |||
| Less Than 90 Degrees | 41.1 | 0.619 | |||
| All | X | 0.619 | |||
The four-seamers outside to righties are, on average, over 6 inches outside, with most thrown, 59.9% to be precise, in the opposite direction of movement. However, most of the pitches thrown in the direction of movement, 31.2%, are thrown with an angle of less than 45 degrees. Compared to LHB, the distances are greater and the percentage of pitches with an angle of less than 90 degrees is noticeably lower.
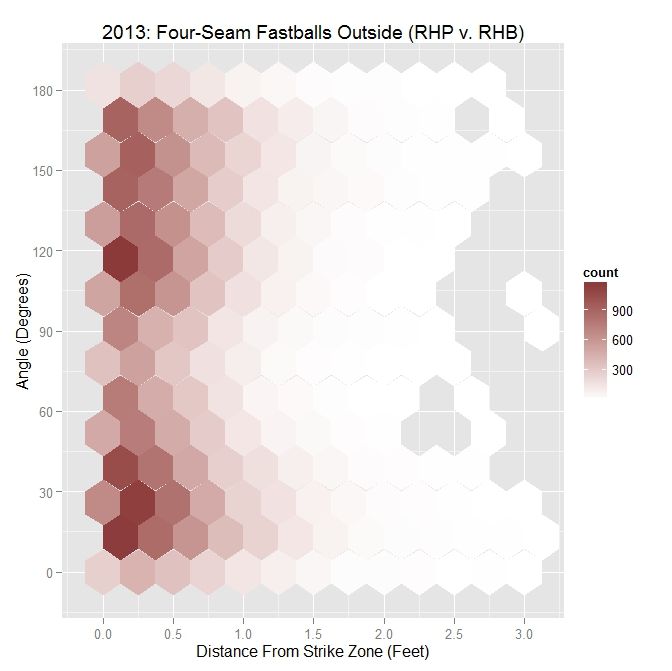
For MLB RHP, the distribution also appears bimodal, with two groupings of data near 30 degrees and 120 degrees. This roughly mirrors Darvish’s distribution, relative to angle versus distance.
| MLB RHP 2013 – Four Seamers Outside the Zone v. RHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 31.6 | 0.514 | |||
| Less Than 90 Degrees | 48.6 | 0.478 | |||
| All | X | 0.476 | |||
As compared to Darvish, RHP threw about the same percentage of pitches with an angle of less than 45%, but more with an angle of less than 90 degrees. In all cases, the MLB RHP four-seamers outside were, on average, closer to the strike zone. Compared to pitches outside to lefties, the percentages for less than 45 and less than 90 degrees are down.
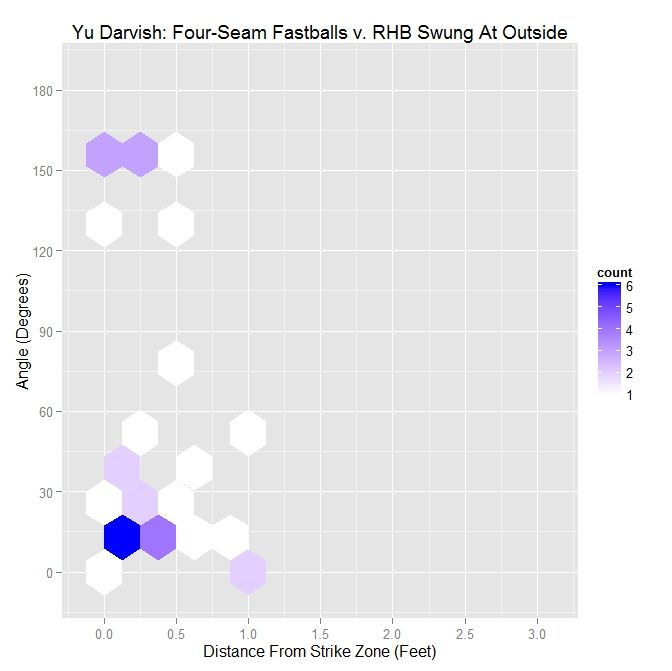
Taking the subset of pitches swung at outside for Darvish, the distribution has become closer to having a single mode near 30 degrees. Despite reaching into small sample sizes for this subset, the below table reinforces these conclusions.
| Darvish – Four Seamers Swung At Outside the Zone v. RHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 67.6 | 0.351 | |||
| Less Than 90 Degrees | 73.5 | 0.347 | |||
| All | X | 0.313 | |||
While only around 30% of Darvish’s pitches were thrown with an angle of 45 degrees or less, over two-thirds of his swings outside the strike zone were in this range of angles. This increases to nearly 75% when considering four-seam fastballs thrown in the general direction of movement, meaning 90 degrees or less. Of note here is that the distance that entices a swing decreases as the movement aligns less and less with the vector perpendicular to the strike zone. Here, the distances are greater compared to left-handed batters faced by Darvish in 2013, but the percentages are up.
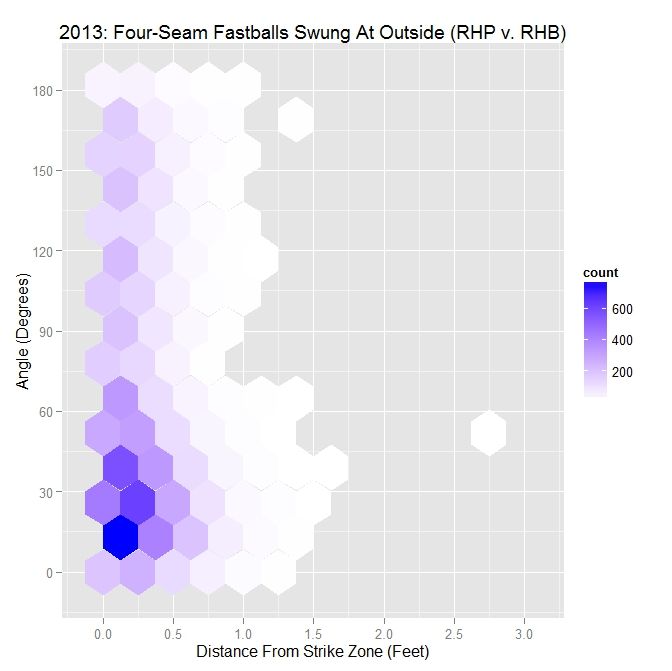
Switching the larger sample of all 2013 MLB RHP, we retain only one of the modes observed for all pitches. The pitches that are swung at outside are clustered down near 15 degrees and within half a foot of the strike zone.
| MLB RHP 2013 – Four Seamers Swung At Outside the Zone v. RHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 53.9 | 0.286 | |||
| Less Than 90 Degrees | 74.2 | 0.268 | |||
| All | X | 0.255 | |||
The percentage of swings with an angle of 45 degrees or less is over 50% and, like Darvish, those less than 90 degrees are up near 75%. The distance again decreases as the angle increases and, compared to Darvish, is much closer to the zone. Versus right-handed batters, the percentages for angles 45 and 90 degrees or less are greater but the distances do not differ greatly as compared to LHB.
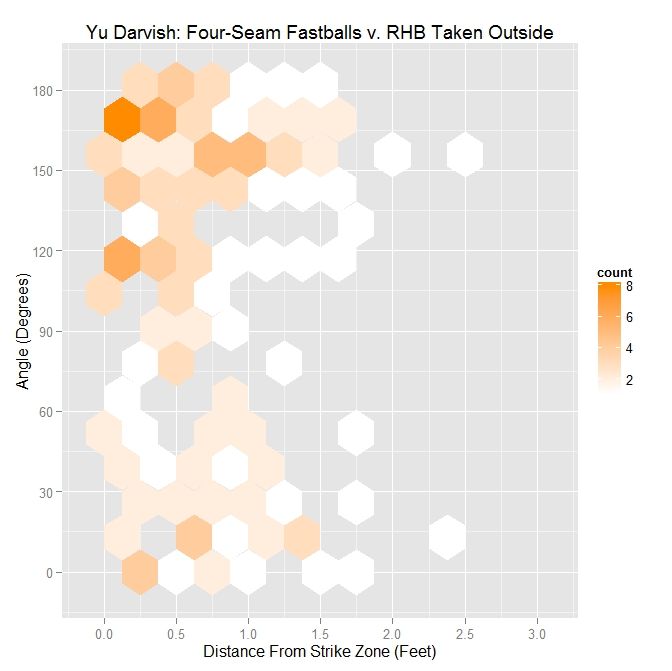
The other half of the data, pitches taken outside, gives us the second mode seen originally in Darvish’s data. This mode is a cluster of data above the 90 degree level.
| Darvish – Four Seamers Taken Outside the Zone v. RHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 23.8 | 0.794 | |||
| Less Than 90 Degrees | 34.5 | 0.736 | |||
| All | X | 0.681 | |||
While a quarter of the pitches taken are thrown with an angle of 45 degrees, only a little over one-third were thrown in the general direction of movement. Note that the pitches that are thrown in the direction of movement and are taken tend to average three-quarters of a foot outside, so it makes sense that they would not be swung at. The percentage of pitches taken with an angle of less than 90 degrees is down from 56.8% for LHB and, overall, the pitches are almost an inch further outside.
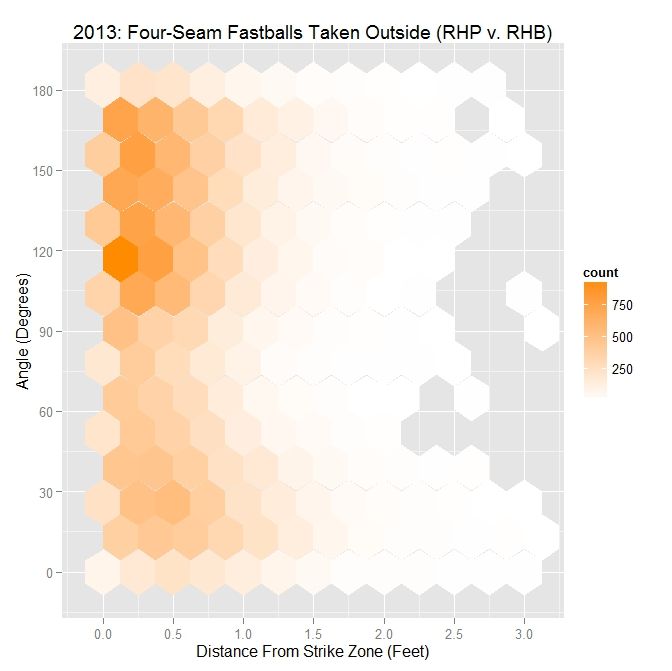
For the MLB data set, the second mode is located around 120 degrees.
| MLB RHP 2013 – Four Seamers Taken Outside the Zone v. RHB | |||||
| Angle | Percentage | Average Distance | |||
| Less Than 45 Degrees | 24.9 | 0.662 | |||
| Less Than 90 Degrees | 41 | 0.592 | |||
| All | X | 0.542 | |||
As with Darvish, about one quarter of the pitches taken outside are at an angle of 45 degrees or less and 59% are thrown in the opposite direction of movement. When put up against the pitches taken by LHB, the percentages are down for both 45 and 90 degree or less pitches from 35.1% and 60.7%, respectively.
As with RHP versus LHB, the full distribution, in terms of the hexplots, separates into two clusters: one related to swings and one related to pitches taken. The cluster related to swings sits in the range of 15 degrees while pitches taken are closer to 120 degrees. This is similar to the case for lefties, except the cluster of pitches taken moves from the 60-degree area to the 120-degree area and the cluster related to swings moves down from 30 degrees to 15 degrees. However, in both cases, the swings appear to be separate clusters from the pitches taken.
Discussion
For four-seam fastballs thrown by Yu Darvish in 2013, the maximum attractiveness on swings is in the range of 10-20 feet in front of home plate for left- and right-handed batters, possibly tying into how long a batter can reasonably project a pitch when deciding to swing. The four-seamers also tend to be swung at outside the strike zone in the general direction of movement, which we have seen previously with sliders. This is especially pronounced for RHB vs RHP, with pitches exiting the strike zone in the direction of movement causing swings, and pitches entering the zone opposite the direct of movement being taken. By simulating the PITCHf/x data, we can get an idea of why this might be true: pitches outside thrown in the general direction of movement project in the strike zone for some period of time before projecting outside of it and pitches thrown opposite this direction project outside and, while their probability increases, these pitches never appear as strikes and thus do not usually induce swings from the batter.
Next time, we will finish up with cut fastballs from Yu Darvish and see how movement affects perception in this case. After that, we can switch to the 2014 data set and also turn the algorithm around and apply it to a batter.
PITCHf/x Simulation
For those familiar with the previous installment, we covered a slider thrown by Yu Darvish to Brett Wallace and simulated the projected pitch location in R. To better represent how the pitch projection may tie into perception, we have switched to a more visually appealing representation of simulating the PITCHf/x data in the context of the catcher’s viewpoint (we could presumably display this from the batter’s point of view as well). For the aforementioned slider to Wallace, the simulated PITCHf/x data, based on the 9-parameter model, is:
This would seem to be a better way to represent the data, including a backdrop and accurate scaling of the pitch size and location. As another example, we can simulate a random Darvish curve:
In order to make the GIFs for simulating the PITCHf/x data, we are first using TeX to write the code and then compiling it using MiKTeX with the “animate” package handling the controls. To begin, we place a reference point 6 feet, 1 inch behind the tip of home plate, roughly approximating the location of the catcher (the one inch past six feet is not important but makes the distance to the front of home plate an even 7.5 feet). The height of the reference point is taken to be 2.5 feet in the z-direction. This is the point by which we will determine perspective. Everything will be projected into the plane at the front of home plate, spanning three feet to the left and right of center and from the ground to five feet high. For a given position of the pitch, we find the associated spherical coordinates, relative to the reference point. To figure out where to display the pitch in the frame, we track the pitch along the line formed between the pitch location and the reference point until it reaches the frame. Since the two angle measures of the spherical coordinates will not change when tracking along this line, we need only find the distance along it that places it in the frame we are displaying.
Once we have the location of the pitch in the frame, we still need to find the size of the pitch as seen from that distance. To do this, we again use the reference point and find the distance to the center and to the top of the baseball. With a third side that goes from the top to the center of the baseball, this creates a triangle. Forming a similar triangle by adding an additional third side where the frame cuts the triangle at the front of the plate, we obtain a smaller triangle contained in the larger one. Using this geometry, we can find the size that the pitch will appear at this distance using trigonometric properties of similar triangles (namely that their sides have the same ratio).
To begin the simulaton, we find the times associated with 55 feet and the front of the plate. We then find the location of the pitch in three dimensions, incrementing in time from release to strike zone and adjusting the location and the size of the pitch to appear positioned and scaled correctly in frame. The simulation in the actual PDF is at 60 frames per second, with most animations lasting around a half a second. For the purposes of creating GIFs, we slow the pitches down to one quarter this speed and capture using a program called LICEcap. The code is written so as to work for any pitch by merely swapping in the chosen 9-parameter PITCHf/x data and recompiling. The projection is shown as a red circle, and is calculated as previously discussed. All background features are scaled appropriately, in a similar manner as the pitch.
Note that while this is, in many ways, an approximation of perception from the catcher’s point of view, it functions well for our purposes of providing a decent replacement for live video since we can overlay the projection and view it from the reverse of the traditional television angle from center field. Included is a link to a Google Drive containing a collection of interactive PDFs for pitchers and pitches from 2013 and 2014. There is also an interactive guide to the controls with the given example being a Clayton Kershaw slider. Finally, the source code is included so the interested reader/programmer can input any chosen PITCHf/x parameters and compile to get a representation of the pitch, that includes distance to home plate, the velocity of the pitch, and the time since release.
Matthew Mata is a mathematician, specializing in applied mathematics and scientific computing. He can be reached via email here. Follow his sporadic tweets on Twitter @arcarsenal8.
Thank you for sharing this extensive analysis in such an accessible way – and sharing how we can explore further and share it ourselves!
Thanks! I’m fine with posting source code if that’s what people are interested in. I also have the side and overhead views of the plate that I was going to use for possibly doing some pitch framing analysis.
I try to work on new ways to approach problems and so it takes me a long time to write the algorithms and results to the point where they’re good enough to publish, but I’m always happy to share anything I’ve got (since it’s better than letting the code fall to disuse just sitting on my hard drive).
excellent stuff
Hey, sorry for the noob question, but how exactly does one run the source code? Like, I plug in my parameters but then how do I compile? Is there something I have to download to run the program? Thanks. The interactive pdfs are mesmerizing (and distracting me from doing work).
Hi,
The code is written in a language called TeX, and the program that I use for compiling it is MiKTeX (miktex.org). If you install it (the program will show up as “TeXworks”) and allow it to download the necessary packages (or you can add them manually), all you need to do is open the file in the program and then hit the green and brown “play” button in the upper-left corner, and it will compile into a PDF. You could also use a number of other programs as well, such as LaTeX.
If you still have trouble, feel free to contact me directly and I can help you through it.
Thanks! I’ll be having a lot of fun with this!
Fantastic article. When I try to run the code I get this error:
! LaTeX Error: File `tikz.sty’ not found.
Any ideas on that one??
For the “File ‘tikz.sty’ not found” error, you’re missing the package that creates the graphics. There are five packages that handle everything within the code: geometry, color, tikz, ifthen, animate. Looking at my setup, I believe that “tikz.sty” is contained in the “PGF” library, which needs to be downloaded separately if your configuration does not download necessary libraries automatically. You can do this by going into the MiKTeX Package Manager and downloading “PGF” (with instruction in the link): http://docs.miktex.org/manual/pkgmgt.html . Hopefully that gets you up and running.
You are very much THE MAN Mr. Mata. That worked. Although I have reached what I hope to be the final obstacle, error:
! Dimension too large.
\pgf@xx
l.124 }
Trying to google my way through it — but if you know an easy fix, that would be huge. Thanks again, loved this article/idea.
Nevermind — figured it!
I got it working too, but it just shows as an image (with magnifying glass), and won’t let me “play” the pitch. The same goes for the images in the google drive. How do you play the animation then? This is cool.
Hi,
To use the controls, you need to open the file in a PDF reader (e.g., Adobe Reader). It won’t play in the preview window of MiKTeX or online. For those on the Google Drive, you need to download them (there should be a download button for each file) and run them locally.