Keeper League Player Depth

by
January 11, 2014

As the second half of the brain trust known as “The ‘I’ in Team is in the A-Hole,” I am tasked with the responsibility of handling the analytic side of our fantasy baseball team. In my continuing preparation for the March draft, I stumbled across an interesting question: What is the best way to prepare for a fantasy draft in a keeper-style league?

From the outside, it is a very easy question to answer. The convenient availability of projections, rankings, and draft cheat-sheets provide a nice guide to determine which players to select. How would you prepare for the draft if the top 150 players were removed from the pool of players before the draft began? This is a challenge that team owners in keeper leagues face. In my league, assuming every owner keeps the maximum of 10 players, the top 100 players will be removed from the talent pool. Drafting in order and ranked by WAR, Starlin Castro would be the first overall pick in the draft. Although this is an exaggeration, it still proves the point I am trying to make. Keeper-league owners need to prepare for the draft differently than traditional redraft-league owners.

I like the umbrella approach WAR has to describing player value. I understand that rotisserie points are dependent on production. WAR provides a measure of general offensive production (wRAA), their ability to advance when on base (UBR and wSB), and their positional value on the field which, theoretically, translates to more playing time (UZR). To test the fantasy relevancy of WAR, I compared 2014 Steamer WAR projections to ESPN’s 2013 end of the year Player Rater. Although not significant, there was a 0.631 correlation. For the most part, the Player Rater aligned fairly well with the player’s projected WAR.

I then took the top 40 players ranked by WAR for positions 2, 3, 4, 5, 6, and DH and selected the top 100 players for the outfield. The total sample was 283 players. On average, Third Base (3B) is the most productive position (2.587) followed by Catcher (C) (2.487) and Outfield (OF) (2.376). To eliminate Mike Trout’s 9 WAR, I broke the position samples into four tiers. Tier 1 included the elite players (Top 25%) with subsequent tiers composed of lesser ranked players. Tier 1 players averaged a 3.88 WAR across the seven measured positions. When breaking the players into performance tiers, we see a significant decline from Tier 1 to Tier 2 (3.887 to 2.422). This is relevant because the majority of kept players will be from the Tier 1 group and will be ineligible for the draft. This decline continues through the four tiers. Third base represents the largest decline in projected WAR at -3.93.

Position

AVG WAR

Tier 1

Tier 2

Tier 3

Tier 4

Third

2.5875

4.75

2.88

1.9

0.82

Catcher

2.4875

4.11

2.74

1.87

1.23

Outfield

2.376

4.084

2.524

1.76

1.136

First

2.0325

3.86

2.28

1.28

0.71

Shortstop

2.005

3.48

2.47

1.49

0.58

Second

1.8975

3.73

2.22

1.08

0.56

DH

1.66

3.2

1.84

1.16

0.44

AVG

3.887714

2.422

1.505714

0.782286

With the elite players gone, how do you decide which players to select? More importantly, how do you determine depth scarcity without the presence of those elite players? First Base (1B) and C represented the highest average WAR across the remaining three tiers (1.947 and 1.867 respectively). You could argue here that reaching for a 1B in the early rounds is unnecessary because there is potential performance deeper in the draft. Surprisingly, 3B also presents an opportunity for those owners without Miguel Cabrera. As a position, Tier 2 and Tier 3 average 2.88 and 1.9 WAR respectively and represent the highest average WAR for each of the collective tiers.

Avg Avail WAR

WAR

Catcher

1.867

First

1.947

Second

1.807

Third

1.423

Shortstop

1.513

Outfield

1.287

DH

1.147

Where is the position scarcity? If you are looking to draft OF, the data indicates you should plan on taking them early. After eliminating the elite players from the sample, OF averages the second-lowest WAR among the remaining tiers (1.287).

Interestingly enough, the data presents some obvious draft windows. For example, Second Base (2B) has one of the lowest average WAR (1.897); but teams need to select either a Tier 1 or a Tier 2 2B as the performance drop is significant (-3.17). Not only does this represent a decline in performance, but it also indicates an obvious area of position scarcity. Injuries here could be difficult to overcome during the season. The data also shows that there is no need to reach on a C or 1B as there will be decent depth throughout the draft. Tier 4 C averaged 1.23 WAR representing the highest value in Tier 4.

Decline

Tier 1

Tier 2

Tier 3

Tier 4

Total

Third

4.75

-1.87

-0.98

-1.08

-3.93

Catcher

4.11

-1.37

-0.87

-0.64

-2.88

Outfield

4.084

-1.56

-0.764

-0.624

-2.948

First

3.86

-1.58

-1

-0.57

-3.15

Shortstop

3.48

-1.01

-0.98

-0.91

-2.9

Second

3.73

-1.51

-1.14

-0.52

-3.17

DH

3.2

-1.36

-0.68

-0.72

-2.76

It is critical to consider the value of your available roster spots. In the same way that MLB teams are looking to maximize their available 27 outs, fantasy owners should consider the value of their 25 available roster spots. An owner would need to roster a Tier 2 and a Tier 3 3B to produce comparable value to a Tier 1 3B. Maximization of available roster spots will provide the owner with the flexibility needed to adapt to the 26-week season.


Pitcher Runs

by
January 10, 2014

Pitching statistics are mostly based on rates. Sure, we have innings pitched, and if you want to annoy me, you can talk about wins and losses, and of course there are the “three true outcomes” of strikeouts, walks, and home runs, plus WAR. But nobody ever looks at how many runs a pitcher was above or below average. Runs allowed isn’t all that common of a statistic; you’re more likely to see ERA or RA9. Even strikeouts and walks are often expressed as a percentage of all plate appearances, or as an amount per nine innings. The defense-independent ERA estimators like FIP and its spinoffs are rates, just like ERA. Where batters have regressed plus-minus or counting stats like wRAA and wRC, pitchers have nothing.

However, there has got to be some value in counting stats for pitchers. If we want to know how many more or fewer runs a team would allow by putting in an average pitcher instead of any given pitcher, that statistic would be able to tell us. So I’m going to present here three basic different numbers, one based off of FIP, one based off of straight runs allowed, and the third based off of linear weights. Each will be in two forms – raw runs allowed and runs allowed above or below average. I’ll call them FIP-Runs and FIP-Runs Above Average (FIPRAA), wRC-Runs and wRC-Runs Above Average (wRCRAA), and, obviously Runs and Runs Above Average (RAA). Kind of long, yeah, but I didn’t want to call the FIP one FRAA because that already exists.

All data was obtained from FanGraphs except for the singles, doubles, triples, home runs, walks, and HBP against used to calculate wRC; FanGraphs does not have some of those so I used Baseball-Reference.

FIP-Runs

This should be pretty simple. Take a pitcher’s FIP. FIP is scaled like ERA, but we want to scale it to RA9 because we want to scale it to all the runs a pitcher allows, not just the earned runs. To do this, multiply it by a constant that changes yearly – for 2013, it was 1.08. This is the league RA9 divided by the league ERA.

Take that figure, multiply it by the number of innings they pitched, and divide by nine to get the number of runs that FIP says a pitcher should have allowed. That’s their FIP-Runs. Great. But now how do we get that to express how many runs above average they were worth?

Well, we already have FIP-, which tells us how much better a pitcher’s FIP was than league average – and it’s already park- and league-adjusted, to boot. So what I did was subtract each pitcher’s FIP- from 200 to get the inverse of their FIP- (so if a pitcher had a 90 FIP-, the inverse would be 110) and multiplied that by their FIP-Runs. That gave me the number of runs (adjusted to the park and league) that an average pitcher would give up in the same number of innings. Just subtract the pitcher’s FIP-Runs, and you have your FIPRAA. And while I was at it, I did the same thing for xFIP. You can find the numbers at the end of the article. But first, the next part:

Runs

I didn’t have to calculate these like I did with FIP-Runs because the numbers are already there – it’s just the total number of runs a pitcher allowed. I did, however, have to calculate RAA, for which I used the same method as I did with FIP-Runs: find the RA9- (this was not park- or league-adjusted because I calculated it myself), take the inverse, multiply it by the runs, and subtract the runs from that. Piece of cake. Now for the last, and hardest, part of this:

wRC-Runs

These were tricky. I had to calculate each pitcher’s wRC against by first finding their wOBA against with the raw number of singles, doubles, triples, etc. they gave up and converting that into wRC. (I’ve actually already put this in a community post in a different form). But from there, I could follow the same instructions as before: use the wRC against as runs allowed, find the wRC/9- (if you didn’t read the article I linked to earlier, wRC/9 is just wRC against scaled like RA/9), and from those two find the wRCRAA (quite a mouthful, I know).

So, without further ado, here are the numbers (sorted by FIPRAA):

Name Team IP FIP-Runs FIPRAA xFIP-Runs xFIPRAA wRC-Runs wRCRAA Runs RAA
Clayton Kershaw Dodgers 236 67.7 23.0 81.6 19.6 40.5 25.1 55 27.4
Max Scherzer Tigers 214.1 70.5 22.6 81.3 16.3 55.4 23.7 73 19.5
Adam Wainwright Cardinals 241.2 74.0 22.2 81.2 21.1 76.2 23.0 83 21.6
Felix Hernandez Mariners 204.1 64.0 21.8 65.2 21.5 69.9 16.9 74 16.3
Anibal Sanchez Tigers 182 52.2 21.4 63.6 16.5 57.8 17.1 56 18.9
Cliff Lee Phillies 222.2 75.4 19.6 74.3 19.3 69.6 21.4 77 19.7
Matt Harvey Mets 178.1 42.8 19.3 56.3 16.9 32.9 19.4 46 20.5
Chris Sale White Sox 214.1 81.5 18.8 75.9 19.0 72.8 18.0 81 15.1
Yu Darvish Rangers 209.2 82.5 18.2 71.5 20.0 66.4 19.8 68 20.5
Jhoulys Chacin Rockies 197.1 82.2 16.4 94.0 -4.7 8.1 7.4 82 8.6
Justin Verlander Tigers 218.1 85.9 16.3 96.2 7.7 95.7 2.7 94 6.9
Jose Fernandez Marlins 172.2 56.6 15.8 63.8 11.5 4.8 4.5 47 19.5
Derek Holland Rangers 213 87.9 15.8 94.1 6.6 95.7 0.4 90 8.1
Doug Fister Tigers 208.2 81.6 15.5 85.6 12.0 96.2 -2.1 91 5.6
A.J. Burnett Pirates 191 64.2 15.4 66.9 15.4 68.2 14.2 79 8.6
Mat Latos Reds 210.2 78.4 14.9 90.0 4.5 79.9 12.7 82 13.3
David Price Rays 186.2 67.9 13.6 73.2 13.2 67.3 13.5 78 7.8
James Shields Royals 228.2 95.2 13.3 102.1 6.1 21.9 17.3 82 18.7
Cole Hamels Phillies 220 86.1 12.0 90.8 8.2 89.2 9.0 94 7.5
Jon Lester Red Sox 213.1 91.9 11.9 99.8 2.0 46.8 24.0 94 4.8
Bartolo Colon Athletics 190.1 73.8 11.8 90.2 0.0 69.1 13.5 60 19.3
Hisashi Iwakuma Mariners 219.2 90.7 11.8 86.5 14.7 66.5 21.9 69 22.3
Clay Buchholz Red Sox 108.1 36.1 11.6 44.3 6.2 24.5 12.2 23 12.5
Francisco Liriano Pirates 161 56.4 11.3 60.3 10.2 53.3 14.2 54 15.0
Patrick Corbin Diamondbacks 208.1 85.8 11.1 87.0 7.0 81.2 11.1 81 13.2
Homer Bailey Reds 209 83.0 10.8 83.8 9.2 76.4 14.5 85 10.6
Stephen Strasburg Nationals 183 70.5 10.6 69.2 11.1 52.3 19.2 71 11.7
Hiroki Kuroda Yankees 201.1 86.0 10.3 87.0 7.8 79.8 9.7 79 12.3
Madison Bumgarner Giants 201.1 73.7 10.3 80.2 9.6 49.2 22.5 68 18.5
Jorge de la Rosa Rockies 167.2 75.7 9.8 82.1 -6.6 75.4 0.2 70 7.1
Rick Porcello Tigers 177 75.0 9.7 67.8 12.9 77.2 2.5 87 -5.1
Jordan Zimmermann Nationals 213.1 86.0 9.5 89.1 7.1 13.3 11.5 81 14.8
Justin Masterson Indians 193 77.6 9.3 77.1 12.3 69.6 14.0 75 12.2
Drew Smyly Tigers 76 21.1 9.1 27.3 6.5 21.2 8.1 20 8.7
Nate Jones White Sox 78 24.7 8.9 25.9 7.8 28.1 5.6 40 -4.2
Koji Uehara Red Sox 74.1 14.4 8.8 18.6 8.7 -0.4 -0.4 10 7.1
Ivan Nova Yankees 139.1 58.0 8.7 61.5 4.3 58.9 3.7 49 11.9
Gerrit Cole Pirates 117.1 41.0 8.6 44.2 7.5 40.0 9.8 43 9.1
Trevor Rosenthal Cardinals 75.1 17.3 8.3 21.2 8.0 24.0 7.0 25 7.1
Mike Minor Braves 204.2 82.8 8.3 89.4 2.7 71.2 16.3 79 13.3
Kenley Jansen Dodgers 76.2 18.3 8.2 19.0 8.7 12.6 8.0 16 8.8
Joe Nathan Rangers 64.2 17.5 8.1 25.4 4.3 0.8 0.8 10 6.7
Adam Ottavino Rockies 78.1 29.6 8.0 33.3 2.0 29.3 5.0 27 7.0
Ricky Nolasco – – – 199.1 79.9 8.0 85.6 4.3 83.6 5.9 90 2.5
Brandon Kintzler Brewers 77 23.5 8.0 27.1 6.0 17.5 8.7 26 7.1
Matt Belisle Rockies 73 26.5 8.0 26.2 5.5 30.6 2.1 37 -3.4
Lance Lynn Cardinals 201.2 79.4 7.9 88.6 2.7 90.4 0.6 92 1.6
Mark Melancon Pirates 71 14.0 7.8 17.5 8.0 12.0 7.5 15 8.2
Corey Kluber Indians 147.1 58.3 7.6 54.8 12.1 69.1 -2.8 67 1.4
Ubaldo Jimenez Indians 182.2 75.2 7.5 79.4 7.1 79.5 2.8 75 8.7
David Robertson Yankees 66.1 20.8 7.5 20.7 7.0 17.3 7.3 15 7.7
Hyun-Jin Ryu Dodgers 192 74.6 7.5 79.7 6.4 69.4 13.8 67 16.7
Craig Kimbrel Braves 67 15.5 7.4 15.7 7.7 9.4 6.5 10 6.8
Andy Pettitte Yankees 185.1 82.3 7.4 86.3 1.7 89.0 -5.7 85 1.1
Tyler Chatwood Rockies 111.1 48.9 7.3 53.4 -3.2 50.7 -0.5 44 6.6
Greg Holland Royals 67 10.9 7.2 13.5 7.7 8.1 5.9 11 7.1
Gio Gonzalez Nationals 195.2 80.1 7.2 82.4 5.8 77.8 9.2 79 10.3
Steve Cishek Marlins 69.2 21.1 7.2 24.9 5.2 2.4 2.2 19 7.8
Alex Wood Braves 77.2 24.7 7.2 29.6 4.7 30.4 4.0 29 5.7
C.J. Wilson Angels 212.1 89.4 7.2 100.1 1.0 92.7 3.0 93 5.3
Neal Cotts Rangers 57 14.8 7.1 19.3 5.6 8.5 5.7 8 5.6
Glen Perkins Twins 62.2 18.7 6.9 19.6 6.7 14.5 7.1 16 7.2
Craig Stammen Nationals 81.2 27.6 6.9 30.2 5.4 31.1 4.8 30 6.3
Zack Greinke Dodgers 177.2 68.9 6.9 73.6 6.6 60.8 14.7 54 18.7
Aroldis Chapman Reds 63.2 18.9 6.8 15.8 7.1 15.9 7.1 18 7.0
Joaquin Benoit Tigers 67 23.1 6.7 25.4 5.1 8.0 5.9 15 7.8
Danny Farquhar Mariners 55.2 12.4 6.6 16.0 6.3 14.2 6.2 29 -3.5
Sean Doolittle Athletics 69 22.4 6.5 30.5 2.1 16.0 7.8 24 6.0
Luke Hochevar Royals 70.1 25.0 6.5 24.5 6.6 12.4 7.6 15 8.1
Anthony Swarzak Twins 96 37.8 6.4 43.9 1.8 33.1 7.8 33 8.6
Ryan Cook Athletics 67.1 22.1 6.4 30.0 1.8 23.9 5.1 22 6.5
Jose Quintana White Sox 200 91.7 6.4 92.6 2.8 5.1 4.8 83 8.8
Alex Cobb Rays 143.1 57.8 6.4 51.9 12.5 49.1 11.8 46 14.2
Steve Delabar Blue Jays 58.2 19.1 6.3 23.6 3.5 14.6 6.5 25 2.1
Henderson Alvarez Marlins 102.2 39.2 6.3 48.9 -2.4 35.5 8.3 42 5.0
Addison Reed White Sox 71.1 27.1 6.2 32.3 1.6 20.3 7.5 31 2.0
Sonny Gray Athletics 64 20.7 6.2 22.4 5.8 17.0 7.0 22 5.7
Alex Torres Rays 58 16.1 6.1 23.0 3.9 7.5 5.3 12 6.7
Brett Cecil Blue Jays 60.2 21.0 6.1 21.8 5.2 16.5 6.6 20 5.8
Rex Brothers Rockies 67.1 27.1 6.0 28.2 2.0 23.1 5.5 16 7.8
Felix Doubront Red Sox 162.1 73.6 5.9 80.6 -3.2 81.9 -9.7 84 -9.6
Mariano Rivera Yankees 64 23.4 5.9 23.7 5.2 18.1 6.8 16 7.4
Wilton Lopez Rockies 75.1 32.3 5.8 33.4 0.7 37.3 -3.7 35 0.0
Junichi Tazawa Red Sox 68.1 26.4 5.8 24.8 5.7 31.3 -0.5 25 5.3
Robbie Ross Rangers 62.1 23.8 5.7 25.4 3.6 26.9 1.1 21 5.8
Fernando Rodney Rays 66.2 22.7 5.7 24.9 5.2 24.4 4.6 27 3.5
Tanner Roark Nationals 53.2 15.5 5.6 20.2 3.4 6.2 4.6 11 6.1
Jason Grilli Pirates 50 11.8 5.6 13.3 5.6 13.2 5.5 15 5.3
Casey Janssen Blue Jays 52.2 17.3 5.5 19.5 4.3 12.0 5.9 17 5.2
Dane de la Rosa Angels 72.1 26.0 5.5 30.3 3.6 18.7 8.0 25 6.4
Luke Gregerson Padres 66.1 21.5 5.4 26.8 3.0 15.8 7.5 24 5.3
David Carpenter Braves 65.2 22.3 5.4 24.5 4.2 13.9 7.4 13 7.5
Scott Kazmir Indians 158 66.5 5.3 63.7 9.6 77.8 -7.2 76 -2.7
Cody Allen Indians 70.1 25.2 5.3 27.6 4.7 27.7 3.5 22 7.2
Tyson Ross Padres 125 48.0 5.3 51.5 4.6 40.4 11.4 51 6.2
Matt Lindstrom White Sox 60.2 22.9 5.3 28.2 0.6 26.2 1.1 23 4.2
Josh Outman Rockies 54 21.1 5.3 23.5 0.9 14.5 5.9 27 -2.1
John Lackey Red Sox 189.1 87.7 5.3 79.3 9.5 4.8 4.6 80 7.2
Charlie Furbush Mariners 65 23.9 5.3 26.3 3.9 13.0 7.2 33 -3.1
Bryan Shaw Indians 75 27.6 5.2 32.2 3.2 21.6 7.8 31 3.4
Jean Machi Giants 53 14.6 5.2 17.7 4.6 8.3 5.4 15 5.9
Will Harris Diamondbacks 52.2 17.3 5.2 19.7 3.4 19.8 3.3 17 5.2
Brian Matusz Orioles 51 17.8 5.2 22.0 2.0 15.6 5.0 21 2.4
Bobby Parnell Mets 50 14.0 5.0 18.3 3.5 9.5 5.5 17 4.6
Aaron Loup Blue Jays 69.1 27.6 5.0 27.5 4.4 24.7 5.2 23 6.6
Kris Medlen Braves 197 82.3 4.9 83.9 5.0 85.4 3.3 77 12.2
Nick Vincent Padres 46.1 11.5 4.9 16.1 3.7 7.0 4.6 11 5.4
Andrew Cashner Padres 175 70.4 4.9 76.0 3.0 58.2 15.3 68 11.1
Sam LeCure Reds 61 21.7 4.8 24.3 2.9 -0.1 -0.1 18 6.6
Tyler Thornburg Brewers 66.2 24.9 4.7 35.4 -6.4 17.9 7.3 17 7.7
Casey Fien Twins 62 23.5 4.7 20.2 6.5 17.2 6.6 28 0.8
A.J. Ramos Marlins 80 31.1 4.7 39.1 -3.1 25.7 7.4 32 4.4
Josh Collmenter Diamondbacks 92 38.3 4.6 44.8 -3.6 27.1 9.4 34 6.9
Mike Dunn Marlins 67.2 25.3 4.6 30.0 0.6 18.7 7.3 21 7.0
Jesse Chavez Athletics 57.1 20.7 4.6 26.4 0.8 20.0 4.5 27 -0.4
Michael Wacha Cardinals 64.2 22.7 4.5 26.1 2.9 75.2 -118.8 20 6.7
Jonathan Papelbon Phillies 61.2 22.6 4.5 26.0 1.8 20.3 5.5 23 4.5
Jamey Wright Rays 70 26.3 4.5 29.2 3.5 -0.4 -0.4 25 5.8
Jim Johnson Orioles 70.1 29.1 4.4 28.5 4.3 19.7 7.5 26 5.3
Dan Otero Athletics 39 9.9 4.4 14.9 3.0 11.8 3.9 7 4.3
J.P. Howell Dodgers 62 21.5 4.3 25.9 2.1 13.3 7.0 15 7.2
Brian Duensing Twins 61 23.7 4.3 27.2 1.6 30.5 -3.3 28 0.3
Jesse Crain White Sox 36.2 6.7 4.2 12.9 3.4 17.2 -0.7 6 3.9
Blake Parker Cubs 46.1 16.1 4.2 19.7 1.2 15.8 3.9 17 3.6
Sergio Romo Giants 60.1 20.6 4.1 23.2 3.5 17.2 6.3 20 5.7
Kevin Siegrist Cardinals 39.2 10.9 4.0 14.3 3.0 3.6 2.9 2 1.8
Jason Frasor Rangers 49 19.8 4.0 21.3 1.9 83.2 -229.7 15 5.1
Jake Diekman Phillies 38.1 11.5 3.9 13.2 3.2 36.2 -39.6 15 2.4
LaTroy Hawkins Mets 70.2 25.9 3.9 26.5 4.5 23.8 6.0 27 4.8
Brad Ziegler Diamondbacks 73 29.8 3.9 29.1 3.5 18.5 8.1 20 8.2
Tim Hudson Braves 131.1 54.5 3.8 56.1 2.8 47.6 9.3 60 1.0
Tommy Hunter Orioles 86.1 38.1 3.8 37.6 3.0 6.7 5.6 28 8.4
Jordan Walden Braves 47 15.8 3.8 19.8 1.4 89.2 -285.9 19 2.5
Dan Jennings Marlins 40.2 13.1 3.8 17.6 0.7 17.6 0.7 17 1.7
Tanner Scheppers Rangers 76.2 34.4 3.8 35.7 0.7 22.1 8.0 21 8.6
Oliver Perez Mariners 53 20.7 3.7 21.4 3.2 25.6 -1.8 23 1.5
Javier Lopez Giants 39.1 11.4 3.6 13.8 3.2 78.9 -271.9 10 4.5
Matt Garza – – – 155.1 72.3 3.6 69.5 2.8 67.9 2.1 73 -0.9
Tony Watson Pirates 71.2 27.5 3.6 32.0 0.3 14.5 8.0 19 8.2
Louis Coleman Royals 29.2 7.3 3.6 9.6 3.1 3.7 2.7 2 1.7
Tim Collins Royals 53.1 21.8 3.5 27.5 -2.2 23.1 0.9 26 -1.3
Roy Oswalt Rockies 32.1 12.0 3.5 13.2 1.3 25.7 -19.5 31 -33.0
Manny Parra Reds 46 16.9 3.4 15.4 4.0 18.4 2.1 18 2.8
Danny Salazar Indians 52 19.7 3.4 17.2 5.1 19.0 3.6 18 4.6
Craig Breslow Red Sox 59.2 25.8 3.4 31.3 -3.1 20.4 5.0 16 6.8
Randy Choate Cardinals 35.1 10.9 3.3 14.0 1.7 7.8 4.0 9 4.1
Antonio Bastardo Phillies 42.2 15.4 3.2 20.9 -1.9 14.9 3.4 12 4.7
Darren O’Day Orioles 62 26.6 3.2 26.7 2.4 18.9 6.1 16 7.1
Yusmeiro Petit Giants 48 16.5 3.1 20.0 1.6 17.3 3.5 19 2.8
Luis Avilan Braves 65 25.6 3.1 31.4 -2.2 9.1 6.3 12 7.2
Sergio Santos Blue Jays 25.2 5.7 3.1 8.0 2.7 -1.1 -1.2 5 2.9
Brandon McCarthy Diamondbacks 135 60.8 3.0 61.1 0.0 68.9 -9.0 71 -9.4
Ervin Santana Royals 211 99.5 3.0 93.4 6.5 79.9 12.9 85 11.3
Chad Qualls Marlins 62 24.7 3.0 24.2 3.4 19.5 5.9 18 6.7
Pedro Strop – – – 57.1 24.4 2.9 22.7 3.4 22.4 3.0 30 -3.8
Vin Mazzaro Pirates 73.2 29.3 2.9 35.4 -2.1 23.8 6.8 23 7.5
Andrew Miller Red Sox 30.2 11.2 2.9 9.0 3.4 12.2 1.4 12 1.9
Brandon Workman Red Sox 41.2 17.2 2.9 15.9 3.2 21.1 -2.6 23 -4.3
Jeff Samardzija Cubs 213.2 96.7 2.9 88.5 7.1 21.1 16.5 109 -10.7
Scott Downs – – – 43.1 16.1 2.9 17.2 2.7 19.0 0.6 13 4.6
Rafael Betancourt Rockies 28.2 11.1 2.9 14.5 -1.7 10.2 2.1 15 -1.9
Paco Rodriguez Dodgers 54.1 20.1 2.8 19.0 4.4 7.5 5.2 15 6.1
Brandon Cumpton Pirates 30.2 9.6 2.8 12.5 1.3 6.3 3.4 8 3.5
Jake Peavy – – – 144.2 68.7 2.7 70.0 -1.4 14.5 11.3 70 -2.9
Bruce Rondon Tigers 28.2 10.4 2.7 11.0 2.1 13.4 -0.5 11 1.9
Caleb Thielbar Twins 46 18.8 2.6 22.9 -0.9 6.2 4.3 11 5.3
Jenrry Mejia Mets 27.1 8.1 2.6 7.6 3.0 106.3 -810.8 9 2.6
Jared Burton Twins 66 28.6 2.6 31.2 0.3 24.3 4.5 29 1.6
Alex Wilson Red Sox 27.2 10.2 2.6 16.0 -3.4 18.1 -8.1 16 -3.9
Shawn Kelley Yankees 53.1 23.2 2.6 20.7 3.7 25.0 -0.9 28 -3.7
Garrett Richards Angels 145 63.7 2.5 62.3 6.2 61.8 3.4 73 -6.1
Jose Mijares Giants 49 17.9 2.5 22.9 -0.9 31.8 -14.0 24 -1.3
J.J. Hoover Reds 66 27.5 2.5 31.4 -1.6 20.7 6.3 21 6.6
Bud Norris – – – 176.2 81.8 2.5 89.5 -5.4 101.3 -27.4 89 -7.5
Jose Veras – – – 62.2 27.2 2.5 29.7 0.0 11.5 6.8 23 4.8
Edwin Jackson Cubs 175.1 79.7 2.4 81.2 -1.6 95.6 -20.0 110 -38.6
Gonzalez Germen Mets 34.1 11.9 2.4 17.1 -1.7 14.6 0.8 15 0.9
David Phelps Yankees 86.2 39.6 2.4 41.9 -0.8 45.7 -7.8 50 -12.1
Ryan Pressly Twins 76.2 33.8 2.4 39.5 -3.2 30.4 3.7 37 -1.4
Grant Balfour Athletics 62.2 26.2 2.4 25.7 3.6 19.7 6.0 20 6.3
Matt Reynolds Diamondbacks 27.1 9.7 2.3 10.9 1.3 9.0 2.4 7 3.1
Chad Gaudin Giants 97 38.9 2.3 46.6 -2.8 34.2 7.5 34 8.3
Jake McGee Rays 62.2 25.6 2.3 23.4 5.1 -0.4 -0.4 28 1.1
Nathan Eovaldi Marlins 106.1 45.8 2.3 53.0 -5.3 42.8 4.6 44 4.8
Brett Oberholtzer Astros 71.2 31.4 2.2 36.7 -2.9 26.0 5.1 26 5.7
Anthony Varvaro Braves 73.1 30.5 2.1 36.9 -4.1 25.8 5.7 25 6.6
Michael Roth Angels 20 5.8 2.1 8.7 0.7 2.4 1.8 16 -11.6
Burke Badenhop Brewers 62.1 26.4 2.1 25.4 2.5 22.2 4.7 32 -3.4
Matt Albers Indians 63 26.4 2.1 28.9 1.2 20.3 5.8 25 3.6
Justin Wilson Pirates 73.2 30.1 2.1 33.8 -0.3 16.9 8.3 17 8.6
Danny Duffy Royals 24.1 9.0 2.1 13.4 -2.1 8.9 1.7 5 2.8
Kelvin Herrera Royals 58.1 25.9 2.1 20.0 5.6 24.5 1.7 27 0.1
T.J. McFarland Orioles 74.2 34.4 2.1 33.0 2.3 36.6 -3.1 37 -2.5
B.J. Rosenberg Phillies 19.2 5.9 2.1 10.1 -1.4 8.3 0.5 10 -0.9
Drake Britton Red Sox 21 7.7 2.0 8.9 1.0 8.9 0.6 9 0.7
Darin Downs Tigers 35.1 15.0 1.9 15.0 1.6 17.9 -2.2 20 -4.4
Fernando Abad Nationals 37.2 14.7 1.9 17.9 -0.9 17.3 -0.3 14 2.8
Will Smith Royals 33.1 14.1 1.8 10.0 3.7 10.1 3.3 16 -0.5
Tom Wilhelmsen Mariners 59 26.1 1.8 32.4 -4.9 45.0 -31.0 28 -0.6
Al Alburquerque Tigers 49 21.9 1.7 20.5 2.5 20.9 1.2 25 -2.5
Taijuan Walker Mariners 15 4.1 1.7 6.8 0.3 3.2 1.7 7 0.0
Ryan Webb Marlins 80.1 34.7 1.7 36.5 -0.4 28.9 5.9 30 5.9
Eric Stults Padres 203.2 86.3 1.7 100.9 -10.1 93.3 -1.4 97 -2.5
Robert Coello Angels 17 5.1 1.7 6.7 1.1 5.7 1.5 7 0.8
Rob Wooten Brewers 27.2 10.6 1.7 14.1 -1.8 9.7 2.2 12 0.8
James Paxton Mariners 24 9.4 1.7 8.9 2.0 18.2 -12.5 5 2.8
Carlos Martinez Cardinals 28.1 10.5 1.7 13.0 -0.3 13.2 -0.4 16 -3.5
Francisco Rodriguez – – – 46.2 20.4 1.6 17.0 3.4 19.4 1.5 14 5.0
Joe Smith Indians 63 27.2 1.6 28.0 2.0 6.8 5.2 17 7.1
Juan Nicasio Rockies 157.2 80.4 1.6 81.7 -12.3 88.9 -22.2 97 -31.5
Kevin Jepsen Angels 36 14.6 1.6 17.0 0.2 18.3 -2.4 21 -5.4
Jim Henderson Brewers 60 25.8 1.5 23.8 2.9 80.2 -157.7 18 6.4
Seth Maness Cardinals 62 25.5 1.5 23.3 4.0 23.8 3.6 17 7.0
Taylor Jordan Nationals 51.2 21.6 1.5 23.6 -0.2 23.7 -0.4 27 -3.4
Brian Wilson Dodgers 13.2 3.3 1.5 4.6 1.2 1.7 1.2 1 0.8
Joe Thatcher – – – 39.1 16.0 1.4 16.8 1.0 22.2 -5.6 14 3.3
Daniel Webb White Sox 11.1 3.2 1.4 4.3 0.9 2.2 1.2 4 1.0
Michael Tonkin Twins 11.1 2.8 1.3 4.8 0.5 3.0 1.2 6 -0.8
Joe Ortiz Rangers 44.2 21.3 1.3 20.5 0.8 6.2 4.3 26 -6.6
Joakim Soria Rangers 23.2 10.5 1.3 10.1 1.0 -0.6 -0.7 10 0.9
Scott Rice Mets 51 20.8 1.2 23.4 -0.2 17.2 4.4 22 1.6
Bobby LaFromboise Mariners 10.2 2.7 1.2 4.5 0.5 4.2 0.5 8 -4.9
Marc Rzepczynski – – – 30.2 12.4 1.2 13.1 1.2 11.3 2.1 13 1.1
Juan Gutierrez – – – 55.1 24.8 1.2 27.2 -0.8 12.6 6.2 29 -3.7
Sean Marshall Reds 10.1 2.5 1.2 3.4 0.9 -0.6 -0.7 3 1.1
Ryan Mattheus Nationals 35.1 14.6 1.2 17.1 -1.2 25.1 -14.3 26 -15.2
Kyuji Fujikawa Cubs 12 4.0 1.1 4.1 1.0 5.2 0.2 7 -1.8
Juan Perez Blue Jays 31.2 14.1 1.1 12.9 1.9 10.9 2.6 17 -2.6
Boone Logan Yankees 39 17.9 1.1 12.7 3.9 14.1 2.8 15 2.6
Drew Storen Nationals 61.2 26.8 1.1 27.5 0.3 29.2 -1.4 34 -6.4
Buddy Boshers Angels 15.1 5.7 1.0 7.9 -0.6 5.7 1.0 8 -1.0
Stolmy Pimentel Pirates 9.1 2.0 1.0 3.8 0.4 0.4 0.4 4 0.3
Dustin McGowan Blue Jays 25.2 11.3 1.0 12.9 -0.8 8.8 2.1 11 0.8
Charlie Morton Pirates 116 50.1 1.0 51.4 1.0 50.6 1.6 51 2.7
Francisley Bueno Royals 8.1 2.6 0.9 4.0 -0.1 -0.6 -0.7 0 0.0
Rafael Soriano Nationals 66.2 29.2 0.9 32.4 -2.3 25.3 4.0 24 5.4
Keith Butler Cardinals 20 7.8 0.9 13.0 -5.9 6.1 2.0 9 0.3
Kris Johnson Pirates 10.1 3.4 0.9 4.9 -0.2 5.2 -0.6 7 -3.2
Sam Freeman Cardinals 12.1 4.4 0.8 6.9 -1.6 9.3 -6.3 3 1.4
Lucas Luetge Mariners 37 16.7 0.8 18.5 -0.9 20.7 -4.9 22 -6.2
David Hale Braves 11 1.0 0.8 1.7 1.1 2.8 1.2 1 0.8
Julio Teheran Braves 185.2 82.2 0.8 83.8 0.0 77.6 5.7 69 13.8
Stephen Pryor Mariners 7.1 1.4 0.8 2.5 0.7 -0.9 -1.2 0 0.0
Luke Putkonen Tigers 29.2 13.6 0.8 12.3 1.6 12.3 1.0 11 2.2
Jimmy Nelson Brewers 10 3.5 0.8 4.5 0.0 2.8 1.1 1 0.8
Jake Petricka White Sox 19.1 8.6 0.8 10.3 -1.2 60.2 -355.1 7 1.5
Charles Brewer Diamondbacks 6 1.7 0.7 2.7 0.0 3.6 -1.1 2 0.6
Wei-Yin Chen Orioles 137 66.4 0.7 68.1 -2.7 69.4 -8.5 62 1.6
Jeremy Jeffress Blue Jays 10.1 4.3 0.6 3.0 1.1 20.3 -67.9 1 0.8
Joel Peralta Rays 71.1 31.5 0.6 36.5 -2.6 9.3 6.6 31 2.0
Yoervis Medina Mariners 68 31.5 0.6 31.4 0.9 22.6 5.9 22 6.7
Ross Detwiler Nationals 71.1 31.3 0.6 36.4 -4.7 42.9 -14.2 37 -4.3
Jon Niese Mets 143 61.4 0.6 65.9 -1.3 97.6 -50.0 68 -1.6
Ernesto Frieri Angels 68.2 30.7 0.6 28.8 3.5 29.1 1.8 29 2.6
Donnie Joseph Royals 5.2 1.8 0.6 2.8 -0.1 1.8 0.5 0 0.0
Luis Perez Blue Jays 5 1.1 0.6 1.6 0.5 1.0 0.6 3 -0.9
Cesar Ramos Rays 67.1 29.9 0.6 32.5 -0.3 25.8 3.9 31 0.3
Carlos Villanueva Cubs 128.2 59.6 0.6 61.3 -3.1 55.6 2.3 58 1.7
Joe Martinez Indians 5 1.1 0.6 2.3 0.1 54.4 -1259.6 1 0.6
Jon Rauch Marlins 16.2 6.9 0.6 8.3 -0.9 10.3 -3.8 14 -11.3
Matt Shoemaker Angels 5 1.4 0.6 2.0 0.3 -0.1 -0.1 0 0.0
Erik Davis Nationals 8.2 0.6 0.5 1.5 0.9 3.8 0.1 3 0.8
Evan Reed Tigers 23.1 10.8 0.5 11.0 0.1 13.5 -3.8 16 -7.6
Michael Kirkman Rangers 22 10.6 0.5 11.7 -1.4 9.3 0.6 20 -19.1
Heath Hembree Giants 7.2 0.6 0.5 1.5 0.8 0.2 0.2 0 0.0
Dellin Betances Yankees 5 1.7 0.5 0.8 0.5 5.1 -6.3 6 -9.5
Mauricio Robles Phillies 4.2 1.3 0.5 2.3 -0.3 3.4 -2.1 3 -1.2
Phillippe Aumont Phillies 19.1 8.3 0.5 10.4 -2.0 14.0 -8.5 11 -2.5
Matt Daley Yankees 6 0.6 0.5 1.3 0.7 -0.3 -0.3 0 0.0
Steven Wright Red Sox 13.1 6.1 0.5 8.4 -2.7 6.4 -0.4 8 -2.3
Tony Cingrani Reds 104.2 47.5 0.5 43.8 3.1 36.4 8.4 37 8.8
Chad Jenkins Blue Jays 33.1 15.8 0.5 17.0 -1.2 13.7 1.2 13 2.1
Kevin Gausman Orioles 47.2 22.8 0.5 17.4 4.0 25.3 -4.5 30 -10.7
Chris Capuano Dodgers 105.2 45.0 0.5 46.5 1.4 55.4 -9.0 57 -9.2
Matt Thornton – – – 43.1 21.0 0.4 21.5 -0.9 21.3 -1.9 20 0.1
Steven Ames Marlins 4 1.2 0.4 1.6 0.2 10.0 -45.4 2 -0.2
Cesar Cabral Yankees 3.2 0.6 0.4 0.8 0.4 1.2 0.3 1 0.4
Neftali Feliz Rangers 4.2 1.8 0.4 3.0 -1.0 2.3 -0.2 0 0.0
Jair Jurrjens Orioles 7.1 3.2 0.4 3.9 -0.5 26.1 -180.0 4 -0.7
Frank Francisco Mets 6.1 2.3 0.4 3.3 -0.5 2.0 0.6 3 -0.1
Chris Dwyer Royals 3 1.0 0.3 1.5 0.0 0.4 0.3 0 0.0
J.J. Putz Diamondbacks 34.1 15.8 0.3 14.0 1.4 18.5 -3.6 9 3.9
Mickey Storey Blue Jays 4 0.4 0.3 1.5 0.3 13.6 -89.1 3 -1.8
Tim Stauffer Padres 69.2 29.7 0.3 26.8 4.0 24.3 5.5 29 3.0
Luis Ayala – – – 33 14.6 0.3 14.9 0.0 16.6 -2.0 12 2.6
Donnie Veal White Sox 29.1 14.2 0.3 13.4 0.5 13.1 0.1 16 -2.8
Vic Black – – – 17 7.1 0.3 9.6 -2.4 8.0 -0.4 7 0.8
Cody Eppley Yankees 1.2 0.4 0.2 0.4 0.2 2.0 -3.3 4 -16.7
Cristhian Martinez Braves 2.1 0.9 0.2 1.0 0.0 2.1 -2.2 2 -1.7
Chris Withrow Dodgers 34.2 14.9 0.1 12.6 2.5 7.5 3.9 10 3.8
Josh Tomlin Indians 2 0.7 0.1 1.6 -1.0 4.7 -19.6 0 0.0
Duke Welker Pirates 1.1 0.2 0.1 0.6 0.0 -0.5 -1.0 0 0.0
Fernando Salas Cardinals 28 12.2 0.1 15.0 -2.9 11.5 1.0 15 -2.3
David Murphy Rangers 1 0.1 0.1 0.3 0.1 0.5 0.0 0 0.0
Ryan Raburn Indians 1 0.1 0.1 0.1 0.1 -0.4 -0.8 0 0.0
Octavio Dotel Tigers 4.2 2.2 0.1 3.2 -1.3 6.8 -15.1 7 -15.6
Jamey Carroll Twins 1 0.4 0.1 0.5 -0.1 93.4 -19255.5 0 0.0
Jake Elmore Astros 1 0.4 0.1 0.5 -0.1 10.0 -210.6 0 0.0
Jose Dominguez Dodgers 8.1 3.5 0.1 5.3 -2.2 8.5 -10.8 3 0.7
Everett Teaford Royals 0.2 0.2 0.1 0.6 -0.5 0.3 0.0 0 0.0
Alex Burnett – – – 2.1 1.1 0.0 1.9 -1.4 3.3 -6.8 3 -5.3
Alberto Gonzalez Yankees 0.1 0.1 0.0 0.3 -0.2 -0.1 -0.3 0 0.0
Sam Fuld Rays 0.1 0.1 0.0 0.3 -0.2 2.4 -35.0 0 0.0
Josh Harrison Pirates 0.1 0.1 0.0 0.3 -0.3 18.5 -2269.2 0 0.0
Andrew Albers Twins 60 28.5 0.0 31.8 -3.5 25.2 1.8 34 -7.5
Brett Anderson Athletics 44.2 20.6 0.0 17.5 3.1 27.1 -9.4 32 -17.4
CC Sabathia Yankees 211 103.8 0.0 95.2 4.8 111.0 -18.4 122 -29.9
Darren Oliver Blue Jays 49 23.8 0.0 22.0 1.3 23.2 -1.1 24 -1.3
David Martinez Astros 11.1 5.3 0.0 6.6 -1.4 8.7 -6.0 11 -12.0
Duane Below Marlins 2.2 1.2 0.0 1.9 -1.0 3.0 -4.4 3 -4.3
Johnny Cueto Reds 60.2 27.7 0.0 23.5 3.3 1.0 0.9 20 5.8
Nick Tepesch Rangers 93 46.8 0.0 42.6 1.7 48.9 -8.0 53 -12.0
Rich Hill Indians 38.2 17.7 0.0 19.1 -0.8 19.0 -1.7 30 -20.1
Shawn Tolleson Dodgers 0 0.0 0.0 0.0 0.0 0.8 #DIV/0! 0 #DIV/0!
Travis Wood Cubs 200 93.4 0.0 108.0 -21.6 70.2 15.6 73 15.6
Logan Kensing Rockies 0.2 0.4 0.0 0.4 -0.1 0.3 0.0 0 0.0
C.C. Lee Indians 4.1 2.1 -0.1 3.2 -1.8 2.5 -0.8 3 -1.5
Brandon Gomes Rays 19.1 8.9 -0.1 7.4 1.5 8.6 0.1 15 -10.1
Evan Scribner Athletics 26.2 12.4 -0.1 14.4 -2.0 13.3 -1.4 13 -0.6
Phil Irwin Pirates 4.2 2.2 -0.2 2.5 -0.5 3.5 -2.3 5 -6.5
Pedro Beato Red Sox 10 5.1 -0.2 6.8 -2.9 5.0 -0.5 5 -0.4
Xavier Cedeno – – – 12.1 5.9 -0.2 7.6 -2.3 8.9 -5.3 12 -13.1
Chris Narveson Brewers 2 1.1 -0.2 1.4 -0.8 0.1 0.1 0 0.0
John McDonald Phillies 0.1 -0.1 -0.2 -0.1 -0.2 9.4 -572.8 0 0.0
Rob Johnson Cardinals 0.1 -0.1 -0.2 -0.1 -0.2 -0.1 -0.3 0 0.0
Rafael Dolis Cubs 5 2.6 -0.2 3.7 -2.4 1.2 0.6 2 0.3
Wesley Wright – – – 53.2 25.2 -0.3 21.4 3.4 28.3 -4.8 24 0.9
Jerry Blevins Athletics 60 27.9 -0.3 30.6 -2.1 92.8 -225.1 23 4.0
Ronald Belisario Dodgers 68 29.7 -0.3 31.3 -0.6 29.8 0.9 34 -2.6
Zach Putnam Cubs 3.1 1.8 -0.3 0.8 0.4 5.2 -12.9 7 -24.7
Shaun Marcum Mets 78.1 34.2 -0.3 39.7 -4.8 38.6 -3.5 48 -15.3
Zach Clark Orioles 1.2 1.1 -0.4 1.7 -2.1 2.1 -3.8 3 -8.6
Neil Wagner Blue Jays 38 18.8 -0.4 16.1 1.8 18.8 -1.9 17 0.6
Joe Savery Phillies 20 9.5 -0.4 10.7 -2.0 127.3 -1669.2 11 -2.0
Phil Coke Tigers 38.1 19.0 -0.4 21.1 -3.4 20.2 -3.3 24 -8.4
Preston Guilmet Indians 5.1 2.8 -0.4 4.4 -3.3 4.5 -4.1 6 -8.5
Jake Odorizzi Rays 29.2 13.8 -0.4 15.4 -1.4 21.1 -12.3 13 0.7
Kevin Slowey Marlins 92 42.1 -0.4 44.3 -3.1 53.2 -14.9 44 -1.3
Manny Corpas Rockies 41.2 22.0 -0.4 20.7 -2.1 18.7 0.1 21 -1.8
Joe Paterson Diamondbacks 2.1 1.5 -0.5 1.8 -1.2 20.1 -363.3 1 0.1
Tyler Lyons Cardinals 53 23.7 -0.5 24.4 -0.5 25.0 -1.2 29 -5.2
Sean Burnett Angels 9.2 4.9 -0.5 4.1 0.4 3.9 0.4 1 0.8
Jaime Garcia Cardinals 55.1 24.7 -0.5 21.7 2.8 58.6 -79.1 26 -0.3
Preston Claiborne Yankees 50.1 25.0 -0.5 23.4 0.5 22.5 0.2 23 0.4
Sandy Rosario Giants 41.2 18.3 -0.5 22.9 -5.0 13.4 3.8 15 3.4
Ryan Brasier Angels 9 4.6 -0.6 4.9 -0.6 3.2 0.7 2 1.0
Javy Guerra Dodgers 10.2 5.1 -0.6 5.2 -0.4 7.0 -3.2 9 -7.4
Miles Mikolas Padres 1.2 1.1 -0.6 1.6 -1.8 0.2 0.1 0 0.0
Edward Mujica Cardinals 64.2 28.8 -0.6 27.4 1.6 22.5 5.1 20 6.7
Arquimedes Caminero Marlins 13 6.4 -0.6 6.8 -1.0 4.0 1.3 4 1.4
Daniel Bard Red Sox 1 0.8 -0.6 1.0 -1.1 1.0 -1.1 1 -1.2
Marco Estrada Brewers 128 59.3 -0.6 55.8 2.2 47.6 8.4 56 3.2
John Gast Cardinals 12.1 5.9 -0.6 6.4 -0.9 78.2 -1020.0 7 -1.6
Brad Hand Marlins 20.2 10.0 -0.6 10.4 -1.3 5.0 2.3 7 1.9
Jeff Beliveau Rays 0.2 0.6 -0.6 0.8 -1.1 24.4 -1953.9 0 0.0
Chris Bootcheck Yankees 1 0.8 -0.6 1.0 -1.1 1.5 -3.6 1 -1.2
Chris Hatcher Marlins 8.2 4.5 -0.6 4.7 -1.0 7.7 -7.4 13 -29.0
Martin Perez Rangers 124.1 63.1 -0.6 60.3 -1.2 60.6 -4.9 55 2.6
Tyler Clippard Nationals 71 32.5 -0.7 34.3 -2.4 12.8 7.7 19 8.1
Josh Zeid Astros 27.2 13.7 -0.7 12.6 0.5 10.9 1.4 12 0.8
Jered Weaver Angels 154.1 70.7 -0.7 79.8 -7.2 9.2 8.0 58 11.1
Alberto Cabrera Cubs 6 3.4 -0.7 4.4 -2.7 5.6 -5.9 3 -0.2
Mike Pelfrey Twins 152.2 73.1 -0.7 83.2 -11.6 92.1 -31.1 92 -27.4
Chris Volstad Rockies 8.1 5.0 -0.7 5.5 -2.6 11.8 -25.5 10 -15.8
Shelby Miller Cardinals 173.1 76.3 -0.8 77.6 0.8 68.8 8.2 65 12.5
Logan Ondrusek Reds 55 26.0 -0.8 22.7 2.0 25.3 -0.5 26 -0.5
Matt Guerrier – – – 42.2 19.6 -0.8 22.7 -4.1 20.1 -0.9 22 -2.4
Scott Atchison Mets 45.1 20.4 -0.8 21.9 -1.5 16.7 3.1 27 -7.6
Josh Lindblom Rangers 31.1 16.6 -0.8 16.9 -2.2 56.7 -170.8 19 -5.8
Simon Castro White Sox 6.2 4.0 -0.8 3.9 -0.9 2.8 0.2 2 0.7
Clay Rapada Indians 2 1.5 -0.8 1.9 -2.0 0.6 0.2 0 0.0
Scott Feldman – – – 181.2 87.9 -0.9 86.3 -1.7 71.5 9.2 87 -2.7
Santiago Casilla Giants 50 22.0 -0.9 25.4 -3.3 14.9 5.1 14 5.6
Brian Omogrosso White Sox 16.1 8.9 -0.9 9.2 -1.7 18.1 -26.4 18 -24.7
Sean O’Sullivan Padres 25 11.7 -0.9 16.9 -8.5 16.4 -7.4 12 -0.4
Kevin Chapman Astros 20.1 10.4 -0.9 12.3 -3.3 5.6 2.2 6 2.2
Wilmer Font Rangers 1.1 1.2 -1.0 1.9 -3.6 0.8 -0.3 0 0.0
Wade Miley Diamondbacks 202.2 96.8 -1.0 91.7 0.0 94.4 -3.1 88 5.7
David Holmberg Diamondbacks 3.2 2.4 -1.0 3.7 -4.7 3.7 -4.5 3 -2.3
Eric O’Flaherty Braves 18 8.9 -1.0 8.2 -0.1 3.5 2.0 5 2.0
Mark Buehrle Blue Jays 203.2 100.2 -1.0 100.0 -3.0 105.4 -15.5 100 -5.7
Ryan Reid Pirates 11 5.7 -1.0 5.6 -0.7 3.9 0.8 2 1.2
Samuel Deduno Twins 108 52.4 -1.0 52.6 -1.1 21.3 12.0 48 2.1
Vidal Nuno Yankees 20 10.8 -1.1 12.8 -4.3 7.5 1.3 5 2.3
Victor Marte Cardinals 3 2.1 -1.2 2.2 -1.4 2.4 -1.9 2 -0.9
Michael Stutes Phillies 17.2 9.1 -1.2 11.5 -5.0 19.1 -26.7 11 -3.7
Bruce Chen Royals 121 59.8 -1.2 71.6 -17.2 45.7 7.4 46 8.3
Tom Gorzelanny Brewers 85.1 40.3 -1.2 37.3 1.1 37.1 1.3 41 -1.4
Steve Johnson Orioles 15.2 8.7 -1.2 8.6 -1.3 22.8 -50.5 13 -10.2
Heath Bell Diamondbacks 65.2 32.3 -1.3 24.3 4.4 38.5 -11.5 30 0.5
Skip Schumaker Dodgers 2 1.6 -1.3 1.9 -2.1 2.4 -3.9 0 0.0
Zach Phillips Marlins 1.2 1.5 -1.3 1.8 -2.4 2.2 -4.3 1 -0.3
Greg Burke Mets 31.2 14.9 -1.3 15.0 -0.8 22.7 -13.4 27 -22.6
Justin De Fratus Phillies 46.2 22.5 -1.3 24.4 -3.9 23.8 -3.1 21 0.7
David Purcey White Sox 25.1 13.7 -1.4 15.7 -4.7 10.0 1.3 7 2.8
Franklin Morales Red Sox 25.1 13.8 -1.4 15.1 -3.8 13.3 -2.2 13 -1.4
Chad Billingsley Dodgers 12 6.3 -1.4 6.7 -1.6 5.9 -0.6 4 1.1
Chaz Roe Diamondbacks 22.1 11.8 -1.4 9.9 0.2 9.0 0.9 10 0.4
Hector Noesi Mariners 27.1 14.3 -1.4 15.5 -3.0 22.0 -17.3 21 -13.7
Pedro Feliciano Mets 11.1 6.1 -1.5 6.5 -1.7 5.9 -0.9 5 0.3
Brandon Beachy Braves 30 14.7 -1.5 13.0 0.5 11.7 1.5 17 -3.7
Kevin Gregg Cubs 62 30.5 -1.5 32.6 -5.2 26.9 1.0 26 2.5
Enny Romero Rays 4.2 3.1 -1.5 3.8 -2.7 0.4 0.3 0 0.0
Blake Wood Indians 1.1 1.3 -1.6 1.5 -2.0 1.2 -1.3 0 0.0
Matt Harrison Rangers 10.2 6.7 -1.6 5.2 -0.1 8.6 -6.7 11 -13.4
Carlos Carrasco Indians 46.2 23.0 -1.6 24.2 -2.2 33.0 -18.6 36 -23.8
Gavin Floyd White Sox 24.1 13.5 -1.6 10.5 0.9 16.8 -8.9 15 -4.9
Cesar Jimenez Phillies 17 9.1 -1.6 11.5 -5.7 7.8 -0.1 7 0.8
Brandon Lyon Mets 34.1 16.4 -1.6 18.5 -3.5 21.0 -7.4 20 -5.1
Josh Edgin Mets 28.2 13.8 -1.7 16.5 -4.4 29.5 -37.8 12 1.2
Alfredo Simon Reds 87.2 41.7 -1.7 44.4 -5.3 28.1 8.1 31 7.4
Yovani Gallardo Brewers 180.2 84.3 -1.7 81.1 0.8 85.3 -4.0 92 -8.9
Zach Duke – – – 31.1 15.8 -1.7 16.4 -2.6 17.7 -4.5 23 -13.4
Aaron Crow Royals 48 25.0 -1.7 22.7 0.2 25.6 -4.7 19 2.8
Chang-Yong Lim Cubs 5 3.5 -1.8 3.8 -2.7 4.9 -5.8 3 -0.9
Robbie Erlin Padres 54.2 25.1 -1.8 26.1 -1.6 23.1 1.5 26 -0.6
Dale Thayer Padres 65 29.6 -1.8 27.7 1.7 26.5 2.5 25 4.3
Jose Cisnero Astros 43.2 22.2 -1.8 22.6 -2.0 25.8 -8.0 23 -3.1
Josh Lueke Rays 21.1 11.2 -1.8 11.7 -1.8 17.4 -13.9 12 -2.5
Jeanmar Gomez Pirates 80.2 37.3 -1.9 38.2 -1.9 12.7 8.3 35 2.3
Jared Hughes Pirates 32 15.8 -1.9 16.6 -2.5 26.4 -22.0 17 -2.4
Kyle Farnsworth – – – 38.1 19.0 -1.9 17.2 0.9 21.6 -5.3 20 -2.5
James McDonald Pirates 29.2 14.7 -1.9 19.2 -8.4 66.7 -265.7 24 -17.8
Jeff Francis Rockies 70.1 38.3 -1.9 32.2 -0.3 1.0 1.0 54 -35.3
Michael Bowden Cubs 37.2 19.4 -1.9 22.8 -7.7 20.5 -4.3 18 -0.5
Jairo Asencio Orioles 2.1 2.2 -2.0 0.9 0.1 5.6 -24.5 2 -1.7
Wade Davis Royals 135.1 67.9 -2.0 67.4 -3.4 89.9 -42.4 89 -37.0
Ross Ohlendorf Nationals 60.1 29.2 -2.0 28.7 -1.4 25.0 2.0 22 4.7
Ross Wolf Rangers 47.2 26.0 -2.1 25.3 -3.0 28.1 -8.5 24 -2.0
Matt Langwell – – – 14 8.2 -2.1 7.7 -1.6 8.0 -2.2 8 -1.8
Cory Burns Rangers 11.1 7.4 -2.1 9.4 -7.0 6.1 -1.2 4 1.0
Alexi Ogando Rangers 104.1 54.6 -2.2 58.1 -9.9 42.6 4.0 38 8.2
Justin Germano Blue Jays 2 2.1 -2.3 1.0 0.0 4.1 -14.5 2 -2.3
Eduardo Sanchez Cubs 6.1 4.5 -2.3 4.6 -2.7 3.5 -0.8 4 -1.4
Chia-Jen Lo Astros 19.1 11.0 -2.3 11.3 -2.6 7.2 1.2 9 0.0
Troy Patton Orioles 56 29.7 -2.4 27.6 -0.8 28.1 -3.2 25 1.0
Hisanori Takahashi Cubs 3 2.7 -2.4 1.8 -0.5 2.2 -1.4 2 -0.9
Adam Warren Yankees 77 39.9 -2.4 36.8 0.0 41.8 -8.5 29 5.5
Jose Ortega Tigers 11.2 7.5 -2.4 6.4 -0.9 33.7 -181.5 5 0.4
Casper Wells – – – 1.2 1.8 -2.4 2.1 -3.8 2.4 -5.1 5 -27.3
Andrew Bailey Red Sox 28.2 16.4 -2.5 11.0 2.1 14.3 -1.5 12 1.2
Brad Brach Padres 31 15.4 -2.5 16.5 -3.0 20.8 -10.1 15 -0.6
Brooks Raley Cubs 14 8.5 -2.5 6.8 -0.5 7.6 -1.5 9 -3.5
Zac Rosscup Cubs 6.2 4.8 -2.7 5.1 -3.5 2.5 0.4 1 0.7
Brad Boxberger Padres 22 11.6 -2.7 10.4 -0.5 11.2 -1.5 9 1.1
David Huff – – – 37.2 20.8 -2.7 16.3 1.5 16.4 0.6 23 -7.2
Jorge De Leon Astros 10 6.7 -2.7 7.6 -4.4 76.9 -1235.0 7 -3.6
Cory Gearrin Braves 31 16.1 -2.7 16.4 -3.0 16.3 -2.7 13 1.3
Jose De La Torre Red Sox 11.1 7.6 -2.7 6.1 -0.9 5.6 -0.5 8 -4.2
Rubby de la Rosa Red Sox 11.1 7.6 -2.7 7.1 -2.3 8.8 -6.4 7 -2.3
J.A. Happ Blue Jays 92.2 47.9 -2.9 53.6 -11.3 49.3 -8.8 53 -12.3
Maikel Cleto Cardinals 2.1 2.3 -2.9 1.1 0.0 4.1 -11.6 5 -18.1
Tyler Robertson Twins 1 1.4 -2.9 0.0 0.0 1.1 -1.6 1 -1.2
Raul Valdes Phillies 35 18.4 -3.0 15.7 0.2 24.8 -14.2 29 -22.7
Rob Scahill Rockies 33.1 19.9 -3.0 17.5 -2.8 22.5 -11.1 19 -4.3
Clayton Mortensen Red Sox 30.1 17.6 -3.0 18.3 -4.9 16.9 -4.0 19 -6.6
Thad Weber – – – 15 9.1 -3.1 7.8 -0.9 7.2 -0.4 5 1.4
Hideki Okajima Athletics 4 3.5 -3.1 2.8 -1.2 3.9 -4.4 1 0.5
Yordano Ventura Royals 15.1 9.8 -3.1 7.9 -0.6 6.7 0.2 6 0.9
Tom Layne Padres 8.2 5.8 -3.3 5.2 -1.8 17.4 -60.4 4 0.0
Alex Colome Rays 16 9.7 -3.3 9.4 -2.2 8.3 -1.3 8 -0.6
Jarred Cosart Astros 60 31.3 -3.4 33.7 -6.1 19.4 5.5 15 6.9
Edgmer Escalona Rockies 46 26.9 -3.5 24.7 -4.7 28.6 -10.7 32 -15.9
Josh Stinson Orioles 17 11.0 -3.5 7.6 0.5 34.1 -117.9 7 0.8
Jake Dunning Giants 25.1 13.6 -3.5 12.8 -1.5 11.3 0.1 8 2.6
Matt Moore Rays 150.1 71.3 -3.6 77.9 -7.0 59.9 7.0 58 9.8
David Hernandez Diamondbacks 62.1 32.6 -3.6 29.8 -1.8 25.8 2.2 33 -4.6
Todd Redmond Blue Jays 77 40.7 -3.7 38.4 -1.9 38.6 -4.3 38 -2.4
Chad Bettis Rockies 44.2 26.4 -3.7 25.1 -6.0 31.0 -16.6 34 -21.7
Dan Straily Athletics 152.1 74.0 -3.7 80.8 -8.9 61.7 6.3 74 -3.4
Hector Rondon Cubs 54.2 28.9 -3.8 29.0 -5.2 25.3 -0.7 29 -4.1
Ian Krol Nationals 27.1 15.4 -3.8 13.3 -1.1 14.2 -2.2 12 0.7
Anthony Bass Padres 42 21.4 -3.8 21.5 -2.8 26.4 -10.4 26 -8.7
Zach McAllister Indians 134.1 65.0 -3.9 73.0 -10.2 68.1 -8.5 65 -2.7
Derek Lowe Rangers 13 9.3 -3.9 6.6 -0.5 9.9 -6.8 13 -15.0
Zach Britton Orioles 40 23.0 -3.9 22.0 -3.5 27.1 -13.6 23 -5.5
Chance Ruffin Mariners 9.2 7.1 -3.9 3.9 0.6 10.1 -13.4 10 -12.3
Aaron Laffey – – – 12.2 8.4 -3.9 8.8 -4.4 12.5 -14.9 10 -7.0
James Russell Cubs 52.2 28.1 -3.9 30.1 -8.1 3.8 3.2 21 3.0
Jonathan Broxton Reds 30.2 17.2 -4.0 16.6 -3.3 13.7 0.2 17 -3.3
Kyle Drabek Blue Jays 2.1 2.8 -4.0 1.5 -0.6 3.5 -8.0 2 -1.7
Daisuke Matsuzaka Mets 38.2 20.0 -4.0 22.3 -6.2 17.1 0.4 21 -3.6
George Kontos Giants 55.1 27.1 -4.1 26.3 -1.3 30.3 -6.4 30 -5.0
Rhiner Cruz Astros 21.1 13.2 -4.1 15.7 -8.5 14.8 -8.0 9 0.8
Mark Lowe Angels 11.2 8.1 -4.2 9.2 -6.0 7.9 -3.9 12 -14.6
Jose Contreras Pirates 5 4.4 -4.3 3.3 -1.5 26.4 -283.4 5 -5.8
Nick Christiani Reds 4 3.9 -4.3 3.3 -2.7 1.8 0.0 1 0.5
Tim Lincecum Giants 197.2 88.7 -4.4 84.4 5.1 86.8 2.3 102 -11.3
Scott Baker Cubs 15 10.2 -4.6 9.9 -4.7 4.4 1.5 6 0.8
John Maine Marlins 7.1 5.9 -4.6 4.1 -1.0 44.4 -552.3 10 -19.4
Jeremy Affeldt Giants 33.2 17.9 -4.7 18.1 -3.4 60.8 -182.4 14 1.5
Nick Hagadone Indians 31.1 18.0 -4.7 17.6 -3.2 14.4 -0.3 21 -9.3
Pat Neshek Athletics 40.1 22.6 -4.7 23.5 -5.2 19.4 -1.3 17 1.6
John Axford – – – 65 33.9 -4.7 27.8 1.7 20.6 6.1 32 -1.9
Justin Grimm – – – 98 54.0 -4.9 49.6 -3.5 65.9 -32.3 70 -37.7
Chris Archer Rays 128.2 62.8 -5.0 60.4 0.6 47.8 8.4 49 8.8
Jonathan Pettibone Phillies 100.1 50.3 -5.0 51.8 -7.2 55.0 -11.8 50 -3.6
Brayan Villarreal – – – 4.1 4.9 -5.1 4.4 -3.8 8.6 -29.5 10 -39.7
Sam Dyson Marlins 11 8.1 -5.1 6.8 -2.5 52.0 -492.9 12 -16.2
Jeremy Horst Phillies 26 15.8 -5.2 16.4 -6.6 94.5 -666.3 19 -10.9
Kyle Kendrick Phillies 182 87.6 -5.3 90.6 -9.1 92.5 -11.7 104 -24.0
Tony Sipp Diamondbacks 37.2 22.1 -5.3 22.6 -7.4 21.8 -6.1 22 -5.7
Ramon Troncoso White Sox 30 19.0 -5.3 17.7 -4.2 16.2 -3.2 22 -12.7
Tyler Skaggs Diamondbacks 38.2 22.6 -5.4 18.3 -0.9 21.1 -4.4 23 -6.5
Kyle McClellan Rangers 9.1 8.0 -5.5 7.1 -4.4 5.5 -1.6 8 -6.8
Erik Johnson White Sox 27.2 17.9 -5.6 15.7 -3.0 17.9 -7.7 16 -3.9
Mike Leake Reds 192.1 93.2 -5.6 90.2 -3.6 85.2 1.5 78 9.9
Jon Garland Rockies 68 40.2 -5.6 37.0 -7.8 28.7 1.8 45 -19.1
Michael Kohn Angels 53 29.0 -5.8 31.2 -7.2 6.3 4.6 22 2.3
Zeke Spruill Diamondbacks 11.1 8.8 -5.8 6.6 -1.9 11.6 -14.8 11 -12.0
Shairon Martis Twins 9.2 8.0 -5.8 5.3 -0.7 4.5 -0.1 6 -2.0
John Lannan Phillies 74.1 39.0 -5.8 42.0 -10.5 81.3 -115.7 48 -18.7
Nick Maronde Angels 5.1 5.2 -5.9 4.3 -2.9 4.0 -2.7 6 -8.5
Josh Roenicke Twins 62 34.5 -5.9 39.4 -13.4 25.2 2.5 31 -2.4
Jason Vargas Angels 150 73.6 -5.9 77.2 -6.2 67.5 0.1 68 1.6
Scott Barnes Indians 8.2 7.2 -5.9 4.0 0.1 6.6 -4.5 7 -5.2
Joe Kelly Cardinals 124 59.7 -6.0 62.3 -6.9 101.0 -81.3 42 11.4
Chien-Ming Wang Blue Jays 27 17.6 -6.0 13.2 -0.4 23.1 -20.7 24 -21.9
Mike Adams Phillies 25 15.8 -6.1 11.4 -0.1 19.6 -14.3 11 0.6
Jeff Manship Rockies 30.2 20.6 -6.2 16.3 -2.9 71.5 -298.2 25 -18.9
Blake Beavan Mariners 39.2 23.8 -6.2 20.6 -1.9 22.9 -6.5 27 -12.6
Tyler Cloyd Phillies 60.1 32.5 -6.2 34.5 -9.3 48.5 -38.0 45 -27.3
Justin Freeman Reds 1 1.9 -6.2 0.9 -0.8 2.0 -6.6 2 -6.6
Chris Resop Athletics 18 12.5 -6.2 11.1 -3.2 13.8 -9.6 13 -7.2
Dallas Keuchel Astros 153.2 78.4 -6.3 66.0 6.6 95.4 -35.9 96 -33.1
Ted Lilly Dodgers 23 14.3 -6.3 13.6 -4.2 16.1 -8.9 16 -8.0
Josh Johnson Blue Jays 81.1 45.1 -6.3 34.9 3.5 -0.1 -0.1 64 -44.4
Hector Santiago White Sox 149 79.4 -6.4 83.1 -14.1 79.0 -13.9 69 0.2
Carter Capps Mariners 59 33.5 -6.4 25.2 2.5 41.4 -22.9 37 -13.0
Colt Hynes Padres 17 11.4 -6.4 10.3 -3.5 15.2 -14.9 17 -19.6
Stephen Fife Dodgers 58.1 30.5 -6.4 27.2 -0.8 35.4 -12.3 28 -0.9
P.J. Walters Twins 39.1 23.7 -6.4 24.6 -7.6 30.1 -20.9 30 -19.3
Jim Miller Yankees 1.1 2.4 -6.4 1.5 -2.0 29.5 -1416.8 3 -11.5
Charlie Leesman White Sox 15.1 11.7 -6.4 10.1 -3.8 20.3 -39.1 14 -13.5
Josh Wall Dodgers 7 6.2 -6.5 4.7 -2.2 0.2 0.2 14 -46.3
Sean Nolin Blue Jays 1.1 2.4 -6.5 1.5 -2.0 5.5 -44.2 6 -52.1
Barry Enright Angels 8.1 7.3 -6.5 5.9 -2.9 9.7 -15.3 12 -25.2
Daniel Stange Angels 1.2 2.7 -6.5 1.6 -1.6 2.2 -4.2 3 -8.6
Sean Henn Mets 2.2 3.4 -6.5 2.5 -2.6 2.9 -4.1 1 0.2
Chad Durbin Phillies 16 11.5 -6.7 8.5 -1.5 16.9 -22.6 17 -21.9
Luis Garcia Phillies 31.1 19.3 -6.7 18.5 -5.7 18.5 -5.8 15 -0.5
Jose Alvarez Tigers 38.2 24.1 -6.7 20.4 -2.2 7.5 4.3 26 -11.6
Trevor Cahill Diamondbacks 146.2 75.0 -6.7 72.3 -6.5 74.3 -9.2 70 -1.9
Tim Byrdak Mets 4.2 4.8 -6.8 3.2 -1.6 4.2 -4.2 4 -3.4
Jeurys Familia Mets 10.2 8.3 -6.8 7.0 -3.2 8.9 -7.7 5 0.0
Eury De la Rosa Diamondbacks 14.2 11.1 -6.8 6.8 -0.1 8.9 -3.1 13 -11.8
Kyle Lohse Brewers 198.2 97.3 -6.8 96.1 -6.7 81.9 7.0 78 12.1
Vinnie Pestano Indians 35.1 21.3 -6.8 19.2 -2.7 23.6 -11.3 18 -1.7
Chris Leroux Pirates 4 4.5 -6.9 3.1 -2.1 4.1 -5.3 3 -1.8
Josh Fields Astros 38 23.3 -7.0 19.2 -1.1 11.2 3.9 21 -4.0
Wandy Rodriguez Pirates 62.2 33.2 -7.0 30.1 -1.8 26.9 1.3 26 2.8
Josh Beckett Dodgers 43.1 24.2 -7.3 19.8 -0.2 19.1 0.5 30 -14.7
Brad Lincoln Blue Jays 31.2 20.8 -7.3 22.5 -11.0 18.8 -5.9 17 -2.6
Dan Haren Nationals 169.2 83.3 -7.5 74.7 2.2 86.3 -11.0 92 -15.4
Brett Marshall Yankees 12 10.3 -7.6 7.9 -3.0 9.2 -6.4 6 -0.5
Hiram Burgos Brewers 29.1 18.9 -7.7 19.0 -8.2 22.1 -14.7 23 -15.8
Collin McHugh – – – 26 18.0 -7.8 14.1 -2.8 26.3 -32.6 29 -40.6
Mike Zagurski – – – 6.1 6.3 -7.8 5.7 -5.6 8.9 -18.9 12 -37.0
Wade LeBlanc – – – 55 31.4 -7.9 33.1 -10.6 38.3 -20.9 40 -22.6
Phil Hughes Yankees 145.2 78.7 -7.9 76.7 -8.4 90.2 -33.7 91 -31.4
Greg Reynolds Reds 29.1 19.0 -8.0 18.1 -6.7 20.0 -10.3 19 -7.5
Zack Wheeler Mets 100 50.0 -8.0 50.5 -6.1 44.6 0.5 42 4.0
Jeff Locke Pirates 166.1 80.4 -8.0 83.6 -9.2 48.9 17.0 69 7.4
Edgar Olmos Marlins 5 5.6 -8.0 3.6 -2.1 5.2 -6.6 9 -25.9
Michael Gonzalez Brewers 50 29.2 -8.2 23.3 -0.7 24.1 -1.7 28 -5.8
Peter Moylan Dodgers 15.1 11.4 -8.2 10.8 -6.0 13.5 -12.8 11 -6.0
Miguel Gonzalez Orioles 171.1 91.5 -8.2 88.6 -8.0 3.6 3.4 81 -1.5
Zach Miner Phillies 28.2 18.7 -8.2 17.1 -5.5 19.9 -10.8 14 -0.7
Michael Blazek – – – 17.1 12.7 -8.3 12.1 -6.7 15.6 -15.6 12 -5.9
Jose Valverde Tigers 19.1 14.8 -8.3 9.5 -0.3 84.6 -736.6 12 -4.0
Chris Rusin Cubs 66.1 37.8 -8.3 35.5 -6.7 33.0 -3.4 30 0.8
Drew Pomeranz Rockies 21.2 16.8 -8.4 14.0 -6.0 19.0 -18.0 15 -7.4
Carlos Torres Mets 86.1 44.5 -8.5 36.3 2.5 35.6 3.1 34 5.2
Erik Bedard Astros 151 79.4 -8.7 83.5 -13.4 86.7 -23.6 83 -15.2
Chris Tillman Orioles 206.1 109.4 -8.8 96.1 1.9 94.6 -1.6 87 8.0
Tommy Hanson Angels 73 40.7 -9.0 42.3 -9.3 25.3 5.9 47 -18.2
Luis Mendoza Royals 94 53.6 -9.1 53.4 -10.1 60.4 -25.7 60 -22.5
Philip Humber Astros 54.2 32.9 -9.2 30.2 -4.8 45.8 -39.1 48 -42.7
Erasmo Ramirez Mariners 72.1 41.9 -9.2 37.0 -2.6 41.8 -11.7 44 -13.6
Ricky Romero Blue Jays 7.1 7.8 -9.3 5.9 -4.0 9.0 -15.5 9 -14.8
Jeremy Bonderman – – – 55 33.8 -9.5 34.1 -10.2 10.8 6.1 36 -14.7
Kyle Gibson Twins 51 31.6 -9.5 29.2 -5.8 39.2 -27.6 38 -23.0
Tom Koehler Marlins 143 73.3 -9.5 73.4 -10.3 72.9 -9.4 72 -6.1
Matt Cain Giants 184.1 86.9 -9.6 85.8 -2.6 71.8 9.8 85 0.6
Jake Arrieta – – – 75.1 43.8 -9.6 41.7 -8.3 2.2 2.1 41 -7.0
Tommy Milone Athletics 156.1 80.7 -9.7 77.9 -3.9 76.2 -6.2 83 -11.9
Anthony Recker Mets 1 2.3 -9.9 1.4 -2.9 1.5 -3.5 2 -6.6
Brian Flynn Marlins 18 13.9 -9.9 10.5 -3.0 19.1 -26.0 17 -17.6
Henry Rodriguez – – – 22 16.2 -10.0 16.7 -11.3 13.6 -5.0 12 -2.1
Pedro Figueroa Athletics 3 4.6 -10.5 1.9 -0.7 5.5 -17.2 4 -7.5
Dillon Gee Mets 199 95.5 -10.5 97.2 -7.8 96.8 -7.6 84 7.7
Jeremy Hellickson Rays 174 88.1 -10.6 86.7 -4.3 65.4 10.9 103 -28.3
Jacob Turner Marlins 118 62.7 -10.7 66.7 -16.7 11.7 9.1 55 -0.2
Kevin Correia Twins 185.1 97.9 -10.8 94.3 -6.6 106.3 -28.9 89 -3.0
Joba Chamberlain Yankees 42 28.4 -10.8 23.2 -3.7 16.1 2.4 23 -4.1
Hector Ambriz Astros 36.1 24.7 -10.9 19.3 -2.1 29.1 -22.6 28 -18.5
Chris Perez Indians 54 32.9 -10.9 24.8 0.7 34.5 -14.4 27 -2.1
Paul Maholm Braves 153 77.8 -10.9 71.4 -2.1 84.0 -18.2 82 -12.6
Carlos Marmol – – – 49 30.5 -11.3 26.6 -5.6 28.5 -8.3 26 -3.7
Guillermo Moscoso Giants 30 20.0 -11.4 20.4 -10.4 14.2 -0.7 17 -3.7
Liam Hendriks Twins 47.1 30.9 -11.4 27.1 -5.4 38.0 -29.5 39 -30.2
David Aardsma Mets 39.2 25.1 -11.5 22.0 -5.1 21.3 -4.0 20 -1.7
Brandon League Dodgers 54.1 32.1 -11.9 26.5 -2.1 34.6 -14.2 37 -17.3
Brandon Morrow Blue Jays 54.1 35.3 -12.0 29.3 -3.8 38.0 -21.0 39 -21.3
Mike Kickham Giants 28.1 19.5 -12.1 11.3 1.4 28.5 -35.2 34 -53.8
Trevor Bauer Indians 17 14.4 -12.1 13.5 -8.9 12.7 -8.3 11 -4.3
Alfredo Figaro Brewers 74 43.2 -12.1 32.3 1.0 36.6 -3.5 41 -7.9
Wily Peralta Brewers 183.1 94.6 -12.3 90.9 -9.1 89.2 -7.1 107 -27.5
Huston Street Padres 56.2 33.5 -12.4 27.2 -1.6 21.6 3.4 17 6.0
Jordan Lyles Astros 141.2 77.7 -12.4 75.0 -8.2 73.3 -10.8 98 -48.0
Ryan Dempster Red Sox 171.1 96.2 -12.5 86.6 -5.2 98.2 -26.6 97 -21.2
Burch Smith Padres 36.1 23.8 -12.6 17.8 -1.6 27.3 -18.2 26 -14.1
Brandon Maurer Mariners 90 52.9 -12.7 45.9 -3.2 65.8 -40.9 66 -38.2
Donovan Hand Brewers 68.1 41.1 -12.7 37.5 -7.9 37.2 -7.7 29 2.5
Vance Worley Twins 48.2 32.3 -12.9 27.8 -5.6 47.5 -55.4 43 -38.8
Bryan Morris Pirates 65 38.1 -13.0 33.9 -5.1 26.8 2.3 25 4.3
Cory Rasmus – – – 21.2 17.2 -13.0 13.5 -4.5 16.4 -11.2 15 -7.4
Esmil Rogers Blue Jays 137.2 78.1 -13.3 67.1 -1.3 81.2 -25.0 76 -14.3
Ethan Martin Phillies 40 27.1 -13.3 21.7 -4.6 28.2 -15.8 27 -12.2
Ramon Ramirez Giants 5.2 7.0 -13.4 5.3 -5.9 7.5 -14.6 8 -16.3
Brad Peacock Astros 83.1 49.8 -13.4 44.4 -5.3 47.7 -12.8 51 -16.2
Allen Webster Red Sox 30.1 23.7 -13.5 18.9 -5.7 25.3 -21.6 30 -33.9
Billy Buckner Angels 17.1 15.3 -14.3 11.6 -4.8 11.9 -6.2 9 -1.1
Deunte Heath White Sox 7.2 9.5 -14.4 8.2 -10.2 8.7 -13.3 10 -18.1
Jarrod Parker Athletics 197 104.0 -14.6 104.3 -11.5 22.7 16.9 92 -0.5
Alfredo Aceves Red Sox 37 28.2 -14.9 22.2 -5.8 29.3 -22.1 21 -4.7
Nate Karns Nationals 12 12.1 -15.0 6.6 -1.4 13.0 -18.2 11 -10.7
Pedro Hernandez Twins 56.2 37.7 -15.1 35.2 -10.5 47.8 -41.5 43 -27.3
Onelki Garcia Dodgers 1.1 3.2 -15.2 1.9 -3.9 2.6 -8.5 2 -4.5
Edgar Gonzalez – – – 18 16.5 -15.2 11.8 -4.4 17.7 -21.0 16 -14.6
Edinson Volquez – – – 170.1 86.7 -15.6 83.2 -6.7 105.8 -39.8 114 -50.3
Eric Surkamp Giants 2.2 4.8 -15.7 3.2 -5.2 7.1 -35.3 7 -32.6
Shawn Camp Cubs 23 19.5 -15.8 13.6 -4.2 21.5 -23.0 18 -12.3
J.C. Ramirez Phillies 24 19.7 -16.0 15.8 -7.2 24.0 -29.1 22 -21.4
R.A. Dickey Blue Jays 224.2 123.5 -16.1 114.0 -8.0 107.4 -6.4 113 -9.4
Andre Rienzo White Sox 56 39.3 -16.5 32.0 -6.4 34.0 -11.7 34 -10.4
Joel Hanrahan Red Sox 7.1 9.9 -16.9 5.9 -4.2 16.8 -68.5 8 -10.8
Mike Fiers Brewers 22.1 19.2 -16.9 11.8 -2.0 35.1 -86.9 20 -18.6
Cole DeVries Twins 15 15.2 -17.2 11.3 -6.4 17.6 -28.2 18 -28.5
Yunesky Maya Nationals 0.1 1.7 -17.3 0.3 -0.3 1.9 -22.9 2 -23.8
Jason Hammel Orioles 139.1 82.4 -17.3 76.2 -11.4 14.4 11.1 81 -20.4
Jake Westbrook Cardinals 116.2 64.7 -17.5 69.3 -22.2 8.7 7.3 69 -18.9
Travis Blackley – – – 50.1 35.8 -17.6 25.4 -1.5 26.8 -4.8 27 -4.2
Jeremy Hefner Mets 130.2 70.4 -17.6 63.5 -5.1 118.9 -120.9 75 -17.7
Ramon Ortiz Blue Jays 25.1 22.6 -18.7 18.2 -9.3 21.9 -20.1 17 -7.6
Randall Delgado Diamondbacks 116.1 69.7 -18.8 55.0 -2.8 59.7 -8.2 59 -5.4
Aaron Harang – – – 143.1 82.4 -18.9 75.3 -8.3 82.9 -23.4 91 -33.4
Pedro Villarreal Reds 5.2 8.4 -19.1 4.2 -2.6 10.4 -32.0 8 -16.3
Roberto Hernandez Rays 151 83.9 -19.3 65.2 5.9 82.9 -17.9 87 -20.9
John Danks White Sox 138.1 84.0 -19.3 67.7 -2.0 37.5 15.0 81 -21.1
Mitchell Boggs – – – 23.1 20.8 -19.3 16.1 -8.5 20.3 -18.9 23 -25.8
Freddy Garcia – – – 80.1 52.9 -19.6 38.6 -0.8 42.0 -6.6 40 -2.9
Bronson Arroyo Reds 202 108.8 -19.6 96.2 -4.8 91.9 -0.8 88 5.5
Jerome Williams Angels 169.1 93.5 -19.6 86.2 -6.0 3.4 3.2 93 -17.0
A.J. Griffin Athletics 200 109.2 -19.7 100.3 -5.0 80.6 8.6 91 1.9
Joe Saunders Mariners 183 103.7 -19.7 92.9 -6.5 1.6 1.6 117 -44.1
Michael Belfiore Orioles 1.1 4.0 -20.0 1.3 -1.5 10.8 -181.4 2 -4.5
Ian Kennedy – – – 181.1 99.9 -21.0 91.2 -10.0 102.9 -26.6 108 -30.5
Alex Sanabia Marlins 55.1 38.8 -21.4 35.2 -14.4 43.2 -31.6 33 -9.4
Johnny Hellweg Brewers 30.2 26.0 -22.3 25.1 -20.3 17.6 -4.8 30 -33.2
Paul Clemens Astros 73.1 50.1 -22.5 44.6 -12.5 49.5 -24.6 48 -19.6
Jeremy Guthrie Royals 211.2 121.7 -23.1 115.6 -17.3 33.9 21.9 99 -0.7
Matt Magill Dodgers 27.2 23.7 -23.4 20.1 -12.2 21.9 -16.6 25 -23.6
Ryan Vogelsong Giants 103.2 61.1 -23.8 56.0 -11.2 68.4 -31.7 73 -37.7
Scott Diamond Twins 131 81.6 -25.3 74.0 -14.1 85.4 -37.9 88 -39.3
Jonathan Sanchez Pirates 13.2 15.9 -26.4 8.1 -2.6 21.9 -56.1 18 -33.0
Dylan Axelrod White Sox 128.1 83.8 -26.8 75.6 -18.1 96.2 -63.7 89 -43.9
Brett Myers Indians 21.1 22.3 -28.4 12.3 -2.6 20.7 -23.8 19 -17.4
David Carpenter Angels 0.1 2.2 -28.4 0.8 -2.9 2.7 -47.3 4 -99.3
Joe Blanton Angels 132.2 81.5 -28.5 61.1 1.8 28.9 14.9 96 -53.6
Roy Halladay Phillies 62 45.7 -28.8 37.9 -13.7 39.7 -16.7 48 -32.0
Dave Bush Blue Jays 3 7.5 -30.5 2.5 -1.9 5.8 -18.9 5 -12.9
Barry Zito Giants 133.1 78.7 -30.7 77.0 -21.5 97.2 -59.8 94 -48.7
Kameron Loe – – – 26.2 26.9 -31.5 15.0 -3.5 28.9 -40.4 21 -14.6
Curtis Partch Reds 23.1 24.7 -32.9 17.0 -10.5 17.4 -11.4 16 -7.6
Clayton Richard Padres 52.2 41.3 -34.3 29.5 -7.1 41.2 -30.3 44 -35.1
Robert Carson Mets 19.2 22.2 -35.9 13.7 -7.6 16.1 -13.2 19 -20.5
Lucas Harrell Astros 153.2 99.9 -38.0 91.6 -22.9 103.7 -51.4 111 -61.6
Jason Marquis Padres 117.2 79.8 -46.3 67.9 -19.0 85.4 -52.1 61 -7.1

There you have it. I have to say, I am surprised a little that the very best pitchers don’t even save their team 30 runs over the course of a season compared to an average pitcher – at least if you trust these numbers. Of course, on the other end, we have pitchers costing their team 50+ runs, but I suppose it’s easier to be bad than it is to be good.

Obviously, the more you pitch, the more these numbers can go up/down, so these shouldn’t be used to draw too many conclusions – I still think the plain old rate stats are better. But this certainly is valuable if you want to know exactly how many runs a pitcher can save. For the record, I would trust the FIP-based one the most, because it is defense-independent while still being descriptive, unlike xFIP; also, it is park- and league-adjusted unlike wRCRAA and RAA. The others obviously have their uses, though. This is not a predictive stat, because it can’t predict innings pitched, but I think it does a pretty good job being a descriptive one.


Analyzing Yoenis Cespedes

by
January 9, 2014

Yoenis Cespedes struggled at the plate this year for reasons unknown to most. Analyzing why he struggled in 2013 versus why he was deemed excellent in 2012 all comes down to sabermetrics. Cespedes’ biggest enemy was actually… himself. Through research and statistics, Cespedes swings at too many inside pitches in an attempt to hit more home runs. The pressure from his overshadowed rookie season may have come back to haunt him this past year. His batting average dropped from .292 to .240 and his OPS fell from .861 to .737 all because of a few changes Cespedes made at the plate. The statistics easily point out the causes for Cespedes’ struggles and how he might be able to fix them for next season. Even though it may seem that Cespedes was a much worse batter in 2013, that is not the entire case. He actually was much better at making contact with pitches thrown to the outside of the strike zone, boasting an increase from 59.5 % to 63.7 %.

   1.  Swinging at Inside Pitches Too Often & Taking Too Many Strikes
Cespedes took a swing at way too many pitches inside the strike zone this season. A number that increased from 65.3 % to 71.8 % from 2012 to 2013. In comparison, when Adrian Beltre took a swing at 71.6 % of inside pitches in 2005, he hit .255 with just a .716 OPS. In addition, when swinging at such a high amount of inside pitches, Cespedes’ hit a lower percentage of them as well — going from 84.0 % in 2012 to 80.4 % in 2013. As a result of his tendency to swing more often at inside pitches, he saw an increase of strikes by 2.5 % (1233 of 1979 in 2012 to 1407 of 2169 in 2013). More strikes lead to more strikeouts and a lower batting average. His strikeout rate increased from 18.9 % to 23.9 % just over the course of a single season.

Swinging at the amount of inside pitches that he did, power pitchers took full advantage of his swing, resulting in a .196 batting average. Against finesse pitchers, Cespedes averaged a .263 batting average. (power pitchers are defined as the top third of pitchers when combining the amount of strikeouts and walks. finesse pitchers are defined as the bottom third) When Cespedes fell behind in the count, he proved to be an easy out; with two strikes and any amount of balls, he batted a horrifying .130. Also, Cespedes is often too eager to swing at the first pitch of a plate appearance when he does not have a trace on the pitcher’s style or location. Swinging at the first pitch resulted in a .209 batting average whilst taking the first pitch resulted in a .252 batting average.

Picture

2.  Pulling Too Hard for Home Runs
Cespedes certainly tried to hit as many home runs as possible this season; he did pass the previous year’s number of 23 by three and his power assuredly grew. As evidenced by his spectacle at the home run derby, Cespedes possesses a strength like few others in the MLB. However, he often tried too hard to get the ball over the wall, resulting in an increase in fly ball rate from 39.9 % in 2012 to 45.6 % in 2013. The pressure to improve from critics and fans alike might have pushed Cespedes into trying to hit more home runs than he possibly could. Given his time on the DL due to nagging hand injuries, it surprised most that he even hit this many home runs — either because of lost time or wrist pain.

                    Picture

                                                             The power is definitely still there

 3.  BABIP (Batting Average on Balls In Play)
Cespedes was also just plain unlucky in 2013. BABIP measures the percent of batted balls that end up as hits — either because of defense, luck, or positioning. Basically two-thirds uncontrollable to the batter and one-third placement of the bat. Cespedes ended the 2013 season with a .274 BABIP; whereas the standard and league average nowadays hovers around .300. In 2012, he finished with a .326 BABIP — a lot luckier than this past year. The second reason (pulling for home runs) most likely factors a moderate amount into the regression too. Unfortunately, the causes of BABIP can disguise a player’s true skill level behind solid defense, timing, and bad luck.

The real Yoenis Cespedes is most likely somewhere in between his two major-league seasons but much closer to his rookie season than 2013. Yoenis Cespedes thrived in the spotlight but collapsed under pressure in 2013. His statistics in the 2013 playoffs alone describe his love of the spotlight (.381/.409/.667). Not only does he play well in the playoffs, but he also crushed everyone else in the home run derby this year. Expect Cespedes to be a big bounce-back candidate in 2014 after he can look at why he struggled at the plate. Upon arriving in America from Cuba as a free agent, Cespedes was hailed as a five-tool player and “arguably the best all-around player to come out of Cuba in a generation.” Don’t give up hope on the Athletics’ outfielder just yet.

For more articles like this, visit my baseball analysis and news website: The Wild Pitch

All statistics courtesy of baseball-reference and FanGraphs:
http://www.baseball-reference.com/players/c/cespeyo01.shtml
http://www.fangraphs.com/statss.aspx?playerid=13110&position=OF


Grading 2013 AL SP Performance with Attention to the 2-D Direction of Batted Balls

by
January 8, 2014

Foreword

Two years ago, I began developing a system for evaluating the performance of minor-league pitchers relative to their minor-league level/league peers. My goals were to use only game data that could be extracted from the MLB Advanced Media Gameday archives for every level of the minors (ruling out any of the pitch-outcome data that is available for AA and AAA games), to ignore whether batted balls went for hits or home runs, and to ignore runs allowed. In brief, the challenge amounts to using whatever else information can be compiled from the game-specific dataset to arrive at the best approximation of the pitcher’s true performance, as judged independent of those factors which tend to fall outside their control (defense, park effects, etc.). What eventually follows are the results of applying the latest iteration of this “Fielding and Ballpark Independent Outcomes” method to 2013’s American League starting-biased pitchers.

Basic Steps of Applying the Method to a League

  1. Download the relevant details of every plate appearance (PA) from the league’s season into a spreadsheet/database
  2. Derive a 24-outs-baserunners-state run expectancy matrix à la Tango in The Book
  3. Quantify how each PA of the season impacted the inning’s run expectancy
  4. Exclude all bunts and foulouts, plus every PA taken by a pitcher
  5. Reweight the proportion of line drives (LD), outfielder fly balls (OFFB), ground balls (GB), and infielder flyballs (IFFB) by ballpark to offset any stadium- or stringer-related anomalies in play event classifications
  6. Referencing the run-expectancy value determined for each PA in Step 3, the corresponding basic description of the play (BB vs HBP vs K vs GB vs IFFB vs OFFB vs LD), and the 2 coordinates indicating where the batted ball was fielded (if there was one), quantify what each of the following 12 general PA event types were worth in terms of runs, on average, for the season: 1) walk or hit-by-pitch, 2) strikeout, 3) IFFB, 4) GB to batter’s pull-field-third of the diamond, 5) GB to batter’s center-field-third, 6) GB to batter’s opposite-field-third, 7) LD to pull-third, 8) LD to center-third, 9) LD to opposite-third, 10) OFFB to pull-third, 11) OFFB to center-third, and 12) OFFB to opposite-third.
  7. For each pitcher in the study sample, tally up the number of each of the 12 event types that they allowed and in each instance charge them with the exact number of runs determined in Step 6 for the corresponding event type; divide the resulting sum by the total number of events to arrive at a single number for each pitcher that quantifies how a PA against them that season should have affected the inning’s run expectancy, on average (the more negative this number the better the pitcher should have performed on the year)
  8. Quantify how high or low the pitcher rated on the value in Step 7 versus the mean of the sample on a standard deviation (SD) basis

What were the 12 Event Types Worth in 2013?

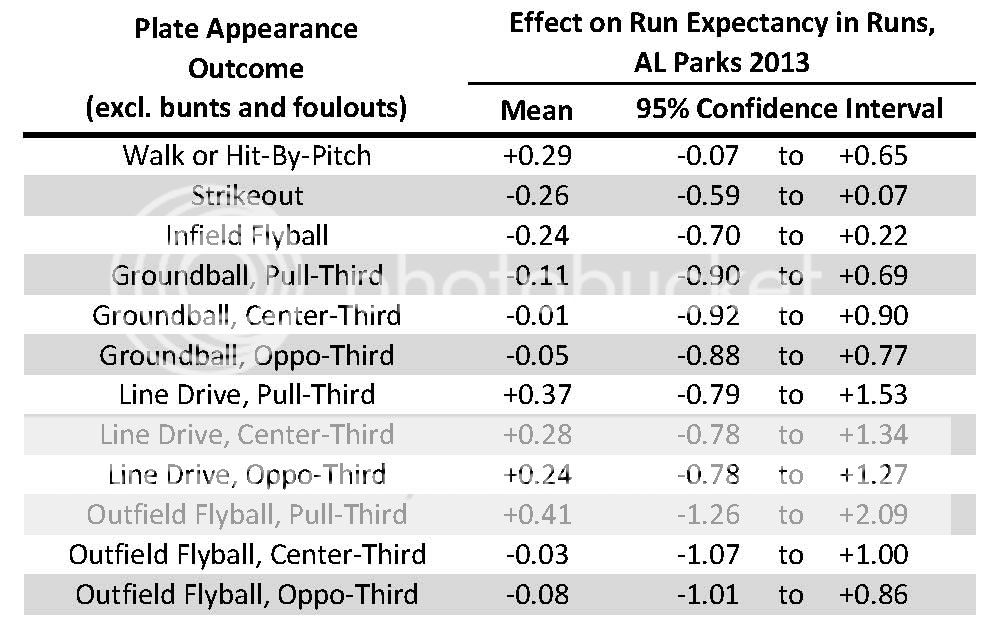
The table below shows how the studied event types impacted run expectancy in AL Parks during 2013, on average. The 2-D direction of the batted ball does tend to be rather consequential for LD and even more so for OFFB.

photo 2013ALParksPAEventType-EffectofRunExpectancies2_zps4e1054de.jpg

So as far as Step 7 described above goes, each pitcher in what follows will be charged +0.29 runs for every BB and HBP, -0.26 runs for every K, … and -0.08 runs for every OFFB to the Opposite-Field-Third, with that sum ultimately divided by the total number of PA events to arrive at a single number that quantifies what an average PA against the pitcher in 2013 was worth in terms of runs (per run expectancies). Think of that as the equation being used to evaluate each pitcher’s performance.

Study Sample

The 101 pitchers who faced more than 200 batters as an American Leaguer in 2013 while averaging more than 10 batters faced per game. Data they accumulated as relievers is included in the analysis. Data they accumulated as National Leaguers is not. As before, any PA that resulted in a bunt or foulout or that was taken by a pitcher was excluded.

Scores Computed

The overall rating number described in Step 8 above is termed Performance Score. Steps 7 and 8 can be repeated with the non-batted-ball events (BB,HBP,K) stricken from the numerator and denominator at Step 7, and this result is termed Batted Ball Subscore (in short, how should the pitcher have rated versus their peers on batted balls?). To further understand how the pitcher achieved their Performance Score, a Control Subscore (how many SDs high or low was the pitcher’s BB+HBP% versus the study population’s mean?) and a Strikeout Subscore (how many SDs high or low was the pitcher’s K% ?) are computed. An Age Score is also calculated that quantifies how young the pitcher was versus the population’s mean age, per SDs. Given the method’s minor-league origins, the scores are typically expressed on a 20-to-80 style scouting scale where 50 is league-average, scores above 50 bettered league-average, and any 10 points equates to 1 SD (percentiles will be listed for those who prefer them).

2013 American League Starting Pitcher Results

In the tables to follow, green text indicates a value that beat league-average by at least 1 SD (“very good”) while red text indicates a value that trailed league-average by at least 1 SD. Asterisks indicate left-handed throwers.

Sorting by Performance Score

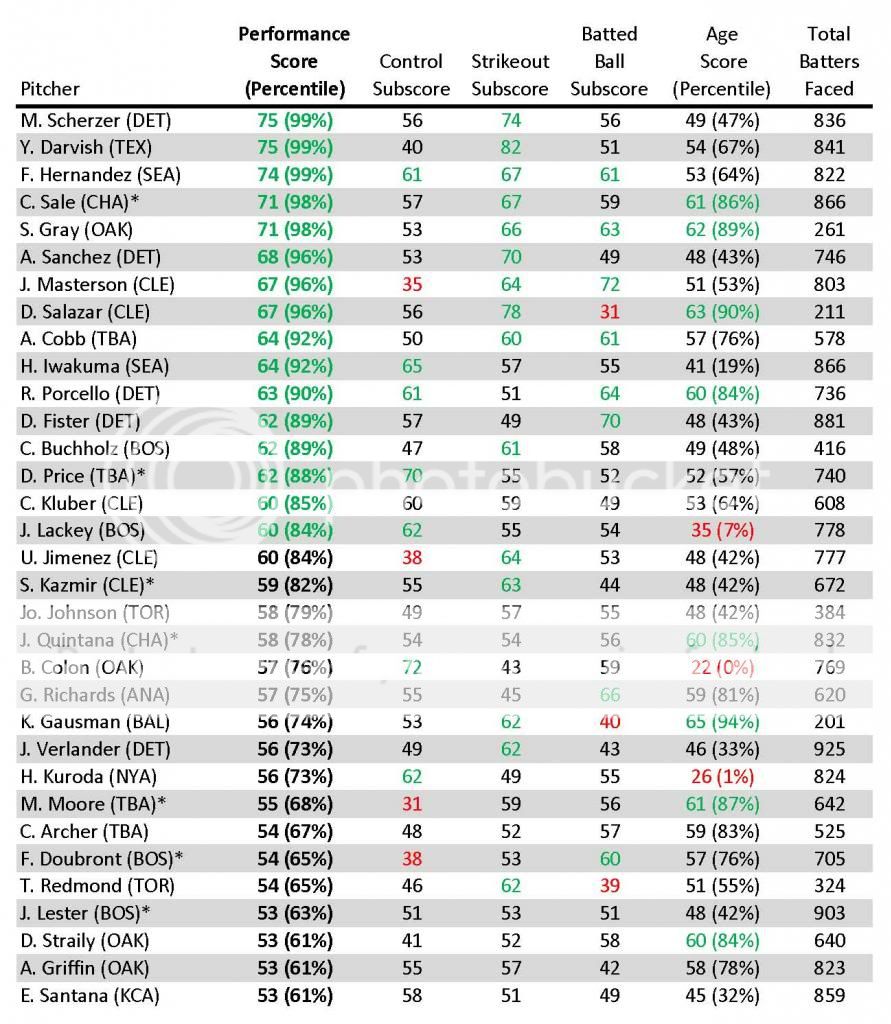
Here are the Top 33 2013 AL SP per the Performance Score measure. Scherzer edged Darvish for the #1 spot as the top of the list somewhat mimicked the BBWAA’s Cy Young vote.

photo FG-2013ALSPScoresTop33_zps7510f67e.jpg

Detroit and Cleveland each landed five in the Top 33 while Boston, Oakland, and Tampa Bay each placed four. Perhaps not coincidentally, those clubs were also the playoff teams.

And below are the Middle 34 by Performance Score.

photo FG-2013ALSPScoresMid34_zps31e63487.jpg

And below are the Bottom 34 by Performance Score.

photo FG-2013ALSPScoresBot34_zps37b53dab.jpg

Pedro Hernandez took last place by a comfortable margin as five other Twins joined him on this dubious list of 34. To further corner the market on these sorts of arms, the club has since inked another of the 34 to a three-year free-agent contract.

Sorting by Batted Ball Subscore

Given the system’s unique weighting of batted-ball types by direction, let us examine how the pitchers grade out on this metric. Below are the Top 20 sorted by Batted Ball Subscore. Masterson nosed out Deduno for top honors. Here, the Twins fare better as three besides Deduno crack the Top 20.

photo FG-2013ALSPBattedBallSubscoresTop20_zps83100793.jpg

 One unique angle of this approach is that a pitcher can be a relatively strong batted-balls performer without being a noteworthy groundball-inducer if their outfield flyballs, line drives, and groundballs are skewed optimally to the least dangerous zones of the field per the batter’s handedness. Colon serves as a prime example of such a pitcher.

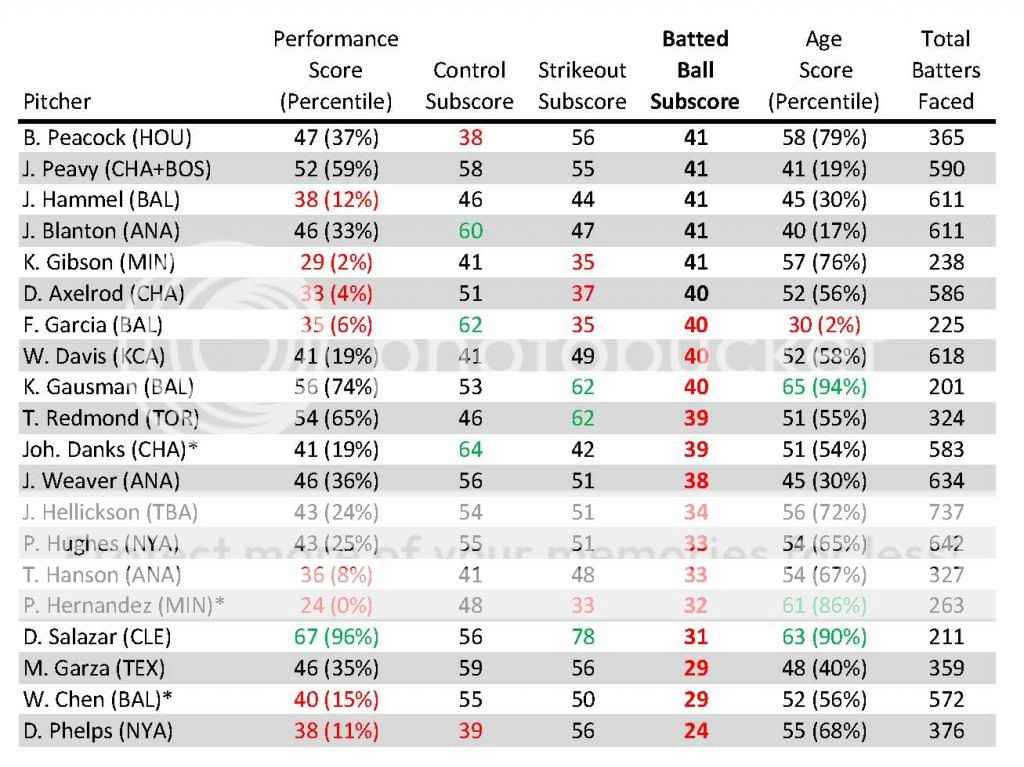
Below are the laggards who comprise the Bottom 20.

photo FG-2013ALSPBattedBallSubscores2Bot20_zps7c4024d0.jpg

Garza’s 29 number as an American Leaguer is somewhat scary for the sort of money he’s likely to command as a free agent (he’d earn about a 35 Batted Ball Subscore if the Cubs NL data were factored in). Salazar’s numbers show how a very high rate of strikeouts and good control can successfully offset a dangerous distribution of batted balls by type and direction.

Admittedly, there is a third dimension to each of these batted balls (launch angle off the bat relative to the plane of the field) that would stand to further improve the batted-balls assessment if such information were available.

Other Directions

A variety of things can be done with these numbers, such as breaking them down further into LHB values and RHB values, identifying comparable pitchers who share similar subscores (MLBers to MLBers, MiLBers to MLBers), studying how these values evolve as the minor leaguer rises through the farm towards the majors and their predictive value as to future MLB performance, and so on. And then there’s also the reverse analysis — evaluating hitter performance under a similar lens.

On Tap

Perhaps the most intriguing research question that application of this system raises is, “Would advanced metrics familiarly used to grade pitcher performance yield better results if their equations included batted-ball directional terms?” As a first attempt to test those waters, I plan to follow this up with a post that shows how these results compare to those obtained by variants of more familiar advanced statistical-evaluation methods (SIERA, FIP, etc.). In the interim, I welcome whatever comments, criticisms, and suggestions this readership has to offer.


Democratic and Fascist Pitchers

by
January 8, 2014

As we all know from the movie Bull Durham, strikeouts are fascist and groundballs are democratic.  So, I want to set out to find the most democratic pitchers and the most fascist pitchers out there.  Luckily, FanGraphs offers a custom leaderboard page that includes batted-ball data.

I set the filters to allow a K/9 rate of 5 or less in a game, a groundball percentage of 50% or greater, and a minimum innings-pitched threshold of 500 innings from 2002-2013.  I realize that five strikeouts a game is kind of arbitrary but I wanted to focus on pitchers who were striking out a batter about every two innings.  You can see the leaderboard for the most democratic pitchers from 2002-2013.

Based on that leaderboard, Aaron Cook should be considered the most democratic pitcher of the twelve-year span, based on his 3.7 K/9 and 57.5% groundball rate.  So, there’s that on his mantle.  Although, I still get confused trying to figure out how Cook was successful. Some other options for most democratic pitcher could be Jake Westbrook and Chien-Ming Wang.  Westbrook had a higher K/9 than Cook but also a higher GB%.  Wang was only slightly higher than Cook on his K/9 but induced groundballs at a slightly higher rate, too.  If you want to say Wang should be more democratic than Cook, far be it from me to stop you.

But, I also wanted to look at pitchers who have had democratic seasons during the span.  So, I created another leaderboard.  Not surprisingly, Cook appears near the top of the leaderboard in terms of value for his democratic season.  Tim Hudson had the most valuable democratic season in 2004, having an fWAR of 4.9.  The difference between 4.9 and 4.5 fWAR, that Cook put up in 2008 is probably not statistically significant.  I feel confident in saying that Aaron Cook is the most democratic pitcher for which we have comprehensive data.

On the flip side of this, I wanted to see who would be considered the most fascist pitchers for which we have data.  To set the parameters, I chose a K/9 of greater than or equal to 10.8 (represents 40% of 27, or how many outs a pitcher can get in a ball game) and a GB% of less than 40% with the same innings requirement as before.  The leaderboard can be found here.

Based on the leaderboard, there are only two fascist pitchers out there: Octavio Dotel and Carlos Marmol.  For some baseball fans, they are essentially the same pitcher and based on the rate stats it is hard to tell them apart.  Dotel was more valuable somehow being able to register a lower FIP than Marmol and pitching about 70 innings more.  So, Dotel is probably a little more fascist based on this stat.

Looking at individual seasons, I chose the same rates but with a minimum of 60 innings pitched.  The leaderboard for individual seasons has a handful of seasons registered by starting pitchers.  By and large, though, these types of seasons are usually only put up by relief pitchers.  Max Scherzer, Rich Harden, and Oliver Perez had more or less the same season in terms of value.  But Rich Harden’s season in 2008 is absolutely stunning.  Look at that low GB%, look how fascist it is.  There are a couple of pitchers on the individual-season list who don’t meet the 500-innings mark in Aroldis Chapman and Kenley Jansen who could also be in the running for most fascist pitchers.  Harden’s individual season was the most fascist, for the purpose of this exercise.  It seems unlikely that a starting pitcher can survive with such a low GB% or keep up such a high K/9 over the course of his career, or a number of seasons.


What Makes a Good Pinch-Hitter?

by
January 7, 2014

There seems to be quite a bit of disagreement in FanGraphs-land over what skills make for a good pinch-hitter. Some will argue that power is more important while others might say that on-base skills are more important. And while I know that it’s fashionable for the author to make a stance at the start of his article, I’m not going comply. I’m just going to unsexily dive face-first into Retrosheet.

How can we solve this problem? How do we know what skills are best for pinch-hitters? Well, we can examine the base-out states that pinch-hitters confront and then derive from those base-out states specific pinch-hitter linear weights. We will then compare pinch-hitter linear weights to league-average linear weights to see which skills retain value. Simple.

We’re also going to split the data by league, since pinch-hitting tendencies in the National League are likely going to be different than American League tendencies. I’m going to use the last five years of data, because whim. The table below, then, includes league-average linear weights followed by NL and AL pinch-hitter linear weights (aside: the run values of linear weights are from 1999-2002, per Tango’s work. This won’t make a real difference in the results, however, since we’re examining relative value of different base-out states and not overall run-value of different events).

Relative Linear Weights, 2009-2013

Linear Weight HR 3B 2B 1B NIBB Out K
League Average 1.41 1.06 0.76 0.47 0.33 -0.300 -0.310
AL Pinch-Hitting 1.45 1.07 0.77 0.49 0.32 -0.305 -0.325
NL Pinch-Hitting 1.42 1.05 0.75 0.48 0.31 -0.290 -0.310

In the National League we can see that the value of home runs have increased slightly while walks have seen a corresponding decrease. This is because pinch-hitters often come to the plate when there are more outs than average. This sensibly decreases the value of walks and increases the importance of hurrying up and sending everyone around the bases already. This note comes with a caveat, however — the differences in linear weights are pretty small. It seems that managers in the National League are often forced to use the pinch-hitter to replace the pitcher, and therefore pinch-hitters are used in a lot of sub-optimal places.

The American league does not condone making everyone hit, however, and the impact upon pinch-hitting situations is pretty clear. The run value of home runs increases by .04 in pinch-hitting situations in the American League compared to the paltry .01 National League increase. In fact the run values of nearly all events increases — managers in the American League simply have more flexibility on when to use pinch-hitters and so they are able to deploy their pinch-hitters in base/out situations that are strategically favorable.

What does this all mean? Like everything, this simultaneously means quite a bit and not much at all. Home run value increases while walk value decreases during average pinch-hitter situations, but the change isn’t huge. If you’re a general manager looking for a bench bat and there’s a home-run guy available with a 90 wRC+ and a plate-discipline guy with a 95 wRC+, take the plate-discipline guy. What if they both have a 90 wRC+? Then take the home-run guy. The pinch-hitter linear weights here are more of a tie-breaker than a game-changer. Power is more important than walks when it comes to being a pinch-hitter, but being a good hitter is more important than power.

Roster construction is never that simple, though. Ideally a team will have both power and plate-discipline guys available on the bench and then the manager will be able to leverage both of their abilities based upon the base/out state (and also the score/inning situation, which is outside the scope of this article). Managers tend to be kind of strategic dunces, though, so I’m not sure if I see this happening. If I were in charge of anything I would supply my manager with a chart of base/out states that list the team’s best pinch-hitters in each situation. I’m not in charge, though, and even if I were I would probably be ignored.

I am in charge of this article, however, which means that I can bring it to a close. I’ll note that another valid way to do this study would be to create WPA-based weights rather than run-expectancy weights. There’s a lot more noise in WPA, but it could still create some interesting conclusions. I reckon the conclusion would be pretty much the same though — what makes a good pinch-hitter? Well, a good hitter makes for a good pinch-hitter. And a little power doesn’t hurt.


The Untold Story of Roberto Clemente’s Plane Crash Litigation

by
January 7, 2014

The Fatal Crash

Roberto Clemente was both a remarkable ballplayer and genuine folk hero. As an outfielder for the Pittsburgh Pirates, Clemente was a perennial All-Star and Gold Glove recipient. He won four batting titles, was the National League’s MVP in 1966 and the World Series MVP in 1971.

Roberto Clemente

On September 30, 1972, Clemente stroked a double off of Mets pitcher Jon Matlack to reach the 3000 hit milestone in his final regular season at bat. After closing out the 1972 season with a playoff series loss to the Cincinnati Reds, Clemente traveled to Nicaragua in November to manage the Puerto Rican All-Stars in the Amateur Baseball World Series.

A 6.2 magnitude earthquake rocked Managua, Nicaragua on December 23, 1972. Some 5,000 people lost their lives, another 20,000 were injured and over 250,000 were displaced from their homes. Swayed by the time he had just spent in Nicaragua, Clemente coordinated a extraordinary effort to provide emergency supplies to the victims. Even after sending three airplane loads to Managua, there were still supplies that needed to be flown to Nicaragua.

Clemente was approached by Arthur Rivera, who offered the services of his DC-7 cargo plane to airlift the remaining relief supplies. Clemente inspected the plane and agreed to pay Rivera $4000 (approximately $22,000 today) upon his return to Puerto Rico.

By law, Rivera was to provide a pilot, co-pilot and flight engineer. Rivera hired a pilot, Jerry Hill, and appointed himself as the co-pilot, despite his lack of certification to co-pilot the DC-7. He was unable to hire a flight engineer for the flight.

Unbeknownst to Clemente, the DC-7 had been involved in an accident on December 2, 1972 when a loss of hydraulic power caused the aircraft to leave the taxiway and crash into a water-filled concrete ditch. After the incident, an airworthiness inspector with the Federal Aviation Administration (F.A.A.) questioned Rivera about intended repairs to the plane. Mr. Rivera confirmed that he intended to repair the plane and the inspector took no further action.

Thereafter, the damaged propellers were replaced and the engines were run for three hours, showing no signs of malfunction. The airplane was returned to service by the repairmen; however, no inspection was conducted by the F.A.A. prior to the ill-fated flight. In fact, the plane had not even been flown since its arrival from Miami in September, 1972.

The loading of Rivera’s DC-7 was completed on December 31, 1972. Clemente decided to personally accompany this flight after having been advised that their prior shipments may not have reached the intended recipients due to governmental interference with the relief efforts.

The flight plan was filed with the F.A.A. on the morning of December 31st. At approximately 9:11 p.m., the flight taxied down Runway 7 and was cleared for takeoff at 9:20 p.m. The weather was good and visibility was at 10 miles.

Upon takeoff, the plane gained very little altitude and at 9:23 p.m. the tower received a message that the plane was turning back around. Unfortunately, the aircraft did not make it, crashing into the Atlantic Ocean about one and a half miles from shore. Everyone aboard the plane, including Roberto Clemente, perished in the crash. He was just 38 years old.

The post-occurrence investigation revealed that there was an engine failure before the crash and that the plane was nearly 4200 pounds over the maximum allowable gross takeoff weight.

Resulting Lawsuit

Vera Zabala Clemente and the next of kin of the other passengers filed a lawsuit against the United States of America alleging that the F.A.A. employees were negligent under the Federal Tort Claims Act and responsible for the resulting crash. (The Federal Tort Claims Act is a limited waiver of sovereign immunity that authorizes parties to sue the United States for tortious conduct.)

Factually, the plaintiffs’ claim was based on the premise that the F.A.A. owed a duty to promote flight safety which was breached by their failure to revoke the airworthiness certificate of the DC-7 after the December 2, 1972 accident; monitor the repair process; and, otherwise discover that the plane was not airworthy, had an improper registration number, was not properly weighted and balanced and did not have a qualified crew. It was the plaintiff’s contention that had the F.A.A. acted in accordance with their own internal procedures (Order SO8430.20C, “Continuous Surveillance of Large and Turbined Powered Aircraft”), the aircraft would have been denied flight clearance, the deceased passengers would have been advised of the deficiencies and that the plane crash would never have happened.

The United States countered that the F.A.A. did not have any legal duty towards the decedents to “discover or anticipate acts which might result in a violation of Federal Regulations.” They also claimed that there was no connection between any duty and the fatal crash.

Who won?

The trial court found for Vera Zabala Clemente and the next of kin of the other deceased passengers on the issue of negligence.

Why?

The trial court was convinced by the F.A.A. investigative report that the cause of the crash was “overboosting” of the No. 2 engine at takeoff and the fact that the plane was overloaded by more than two tons. Because the flight crew was inadequate, the situation was such that “…for all practical purposes the Captain was flying solo in emergency conditions.”

Section 6 of Order SO8430.20C called for “continuous surveillance of large and turbine powered aircraft to determine noncompliance of Federal Aviation Regulations.” Furthermore, a “ramp inspection” was required to determine that the crew and operator were in compliance with the safety requirements regarding the airworthiness of the aircraft as to the weight, balance and pilot qualifications. Any indication of an “illegal” flight crew was to be made known to the crew and persons chartering the service. Finally, discovery of such noncompliance was to be given the highest priority, second only to accident investigation.

The trial court found that these provisions of the Continuous Surveillance of Large and Turbined Powered Aircraft order were applicable to Roberto Clemente’s chartered flight and that the decedents were within the class of people sought to be protected under the order. If the required ramp inspection had been completed, the lack of a proper crew and overloading would have been discovered, Clemente would have been notified and, presumably, he would not have agreed to board the plane and avoided his untimely death.

The order was held to be mandatory in nature and because the F.A.A. violated its own orders, a failure to exercise due care was evident. Accordingly, the F.A.A.’s failure to inspect and ground the plane “contributed to the death of the…decedents.”

The appeal

The United States appealed the decision claiming that the trial court erred in its finding of a duty on the part of the Federal Aviation Administration. The critical question the appellate court was asked to address was whether the F.A.A. staff in Puerto Rico had a duty to inspect the subject DC-7 and warn the decedents of “irregularities.”

The appellate court acknowledged that the Federal Aviation Act was enacted to promote air safety but that this “hardly creates a legal duty to provide a particular class of passengers particular protective measures.” Further, the issuance of the Continuous Surveillance of Large and Turbined Powered Aircraft order was done gratuitously and did not create a duty to the decedents or any other passengers.

The court ultimately held that the order created a duty of the local inspectors to “perform their jobs in a certain way as directed by their superiors.” The failure to comply with this order, however, was grounds for internal discipline but did not create a cause of action based on negligent conduct against the F.A.A.

It is well-founded that the pilot in command has responsibility to determine that an airplane is safe for flight. There was nothing in this F.A.A. directive that shifted this responsibility to the federal government.

Further, the court found that the failure of the F.A.A. to inspect the plane did not add to the risk of injury to the passengers and there was no evidence that any of the deceased had relied on the F.A.A. to inspect the aircraft prior to takeoff or even knew about Order SO8430.20C.

Who won the appeal?

The United States. The finding of negligence on the part of the Federal Aviation Administration was reversed.

In its opinion, the appellate court concluded, “The passengers on this ill fated flight were acting for the highest of humanitarian motives at the time of the tragic crash. It would certainly be appropriate for a society to honor such conduct by taking those measures necessary to see to it that the families of the victims are adequately provided for in the future. However, making those kinds of decisions is beyond the scope of judicial power and authority. We are bound to apply the law and that duty requires the reversal of the district court’s judgment in favor of the plaintiffs.”

The plaintiff’s request that the case be heard by the United States Supreme court was denied.


Billy Hamilton: 2014 Leadoff Hitter?

by
December 31, 2013

The signing of Shin-Soo Choo gives the Rangers a player with strong on-base skills, solid power, and decent corner-outfield defense. The signing also left a gaping hole in the outfield for the Reds. Choo was one of three Reds starters that got on base at an above-average clip. He was easily the first- or second-best offensive player for the Reds in 2013. While he was miscast in center field, Choo brought a great deal of value to a team that needed his particular offensive skill set.

Walt Jocketty has stated that Billy Hamilton is the new center fielder and will likely bat leadoff for the 2014 Reds. Hamilton starting in center field should come as no surprise as the Reds do not have many other options. The wisdom of Hamilton batting leadoff is at least up for debate. You can easily go look at his projections for 2014 and draw your own conclusions, but I would like to at least provide some context.

Every baseball fan knows about Hamilton’s speed. He is ferociously fast. He stole 155 bases in the minors in 2012 and successfully stole 13 bases in 14 attempts in limited major league action in 2013. Speed is nice , but it is certainly not close to the most important skill for a player in the leadoff spot. Reds fans may know this best of all from watching Corey Patterson, Willy Taveras, and Drew Stubbs flounder at the plate. Those players were wickedly fast, but as the saying goes, you can’t steal first base. None of them had the on-base skills to bat leadoff, but they found themselves there anyway because of their speed. To avoid this list of failed Reds leadoff hitters, Billy Hamilton will need to get on base enough to justify being at the top of the order. That is the obvious question: can Hamilton get on base to use that blinding speed of his to turn singles into doubles and doubles into triples? There are signs that he can but others that he shouldn’t in 2014.

The 2012 season launched Hamilton into top-20 prospect territory. He obviously broke the stolen-base record, but he also showed some ability with the bat. In a 132 games between high A and AA, Hamilton hit .311/.410/.420. He had 14 triples. His walk rate rose dramatically from the year before. Hamilton looked like a perfect leadoff hitter through two levels.

Then 2013 and AAA came. Hamilton slashed .256/.308/.343. His walk percentage dropped from 16.9% in 50 games in AA (small sample size noted) to 6.9% in 123 games in AAA. it was arguably his worst season as a professional. He looked completely overmatched at times and questions about his ability to get on base resurfaced.

So which is the real Billy Hamilton, and what does it mean for 2014? Hamilton’s ceiling is likely between his 2012 and 2013 minor league performance. In five seasons as a minor leaguer, Hamilton slashed .280/.350/.378. Coupled with his speed and potential excellent defense in center field, that slash line could make him an All-Star-caliber player. The hope is that 2013 was a product of learning a new position and a significant drop in BABIP from over .370 to .310.

Still, Hamilton was very inconsistent at the plate in 2013 and didn’t prove he could hit AAA pitching for an extended period of time. The major leagues are an obvious step up in competition, and it would be surprising to see him match his .280/.350/.378 minor league career slash line in 2014. Steamer projects him to have a .305 OBP, and after last year, it is easy to see why.

While it is very possible Hamilton could surpass gloomy projections, the Reds probably shouldn’t risk it in 2014, at least at first. It makes much more sense to see how Hamilton adjusts to major-league pitching in a less important part of the lineup (7th for instance). He would get fewer at bats and would not be so heavily scrutinized if he struggled adjusting to the level. If he performs well, he can always move up in the lineup, but the Reds likely have better leadoff options than Hamilton to begin the year.

If Hamilton plays excellent defense in center field and has a good year on the bases, he will provide solid value for the Reds. To fill Choo’s shoes, he will have to hit closer to his career minor league mark as opposed to his 2013 numbers. In 2014, that may be difficult.


The Cascading Bias of ERA

by
December 26, 2013

There are so many problems with ERA that it’s unbelievable. I’m not going to sit here and tell you what’s wrong with ERA, though, because you’re probably smart. But there’s a problem with ERA, and it’s a problem that transcends ERA. It’s a problem that trickles down through FIP, xFIP, SIERA, TIPS, etc. etc. name your favorite stat, etc., and it’s something I don’t see talked about much.

All of our advanced pitcher metrics are trying to predict or estimate ERA. They’re trying to figure out what a pitcher’s ERA should be, and herein lies the problem: Because they could be exactly right, but they’d still be a little incorrect due to one little assumption.

This assumption–that pitchers have no control over whether or not the fielders behind them make errors–seems easy to make. Like most assumptions, however, this one is subtly incorrect. Thankfully, the reason is pretty simple. Ground balls are pretty hard to field without making an error, and fly balls aren’t. And the difficulty gap is pretty huge.

How big? Well in 2013 there were precisely 58,388 ground balls, 1,344 of which resulted in errors. On the other hand a mere 98 out of 39,328 fly balls resulted in errors. That means that 2.3% of ground balls result in errors while a tiny 0.25% of fly balls do. It’s time to stop pretending that this gap doesn’t exist, because it does.

So now that we know this, what does it mean? Well it means this: ground-ball pitchers will have an ERA that suggests they are better than their actual value, while fly-ball pitchers have the opposite effect. Pitchers who allow contact, additionally, are worse off because every time they allow contact they put pressure on their defense. They’re giving themselves a chance to stockpile unearned runs which nobody will count against them if they’re only looking at ERA derivatives. When it comes to winning baseball games, however, earned runs don’t matter. Runs matter.

I am going to call this the “pressure on the defense” effect, which will cause some pitchers to be more prone to unearned runs than other pitchers. How big is this effect? Well, not huge. The gap between the best pitcher and worst pitcher in the league is roughly three runs over the course of the season. But keep in mind that three runs is about a third of a win, and a third of win is worth about $2 million dollars. We’re not discussing mere minutiae here.

In order to better quantify this effect I have developed the xUR/180 metric, which will estimate how many unearned runs should have taken place behind each pitcher with an average defense. Below is a table of all qualified starting pitchers from 2013 ranked according this metric. I have also included how many unearned runs they actually allowed in 2013, scaled to 180 innings for comparative purposes.

# Name xUR/180 UR/180
1 Joe Saunders 7.24 9.84
2 Jeff Locke 7.11 4.33
3 Wily Peralta 6.97 17.7
4 Edwin Jackson 6.88 13.36
5 Edinson Volquez 6.81 6.35
6 Kyle Kendrick 6.77 8.9
7 Justin Masterson 6.66 0.93
8 Doug Fister 6.58 5.19
9 Wade Miley 6.57 7.12
10 Rick Porcello 6.51 2.03
11 Jerome Williams 6.47 7.45
12 Jorge de la Rosa 6.43 5.38
13 Yovani Gallardo 6.42 7.99
14 A.J. Burnett 6.35 8.48
15 Scott Feldman 6.32 8.94
16 Mike Leake 6.26 5.62
17 Andrew Cashner 6.25 8.23
18 Felix Doubront 6.22 6.66
19 Jhoulys Chacin 6.13 5.48
20 Kevin Correia 6.13 2.92
21 Jeremy Guthrie 6.13 3.41
22 Mark Buehrle 6.11 5.31
23 Andy Pettitte 6.05 7.78
24 Hyun-Jin Ryu 6.01 2.81
25 Jeff Samardzija 6.0 5.07
26 C.J. Wilson 5.93 11.03
27 CC Sabathia 5.9 8.53
28 Jon Lester 5.84 4.22
29 Ryan Dempster 5.8 10.52
30 Tim Lincecum 5.77 5.48
31 Hiroki Kuroda 5.72 4.48
32 Bud Norris 5.72 7.15
33 Jordan Zimmermann 5.69 3.38
34 Patrick Corbin 5.68 1.73
35 Dillon Gee 5.67 3.62
36 Ervin Santana 5.67 7.68
37 Kris Medlen 5.66 8.22
38 Bronson Arroyo 5.63 2.67
39 Stephen Strasburg 5.62 9.84
40 Mat Latos 5.62 6.85
41 Ubaldo Jimenez 5.61 7.9
# Name xUR/180 UR/180
42 Jarrod Parker 5.61 4.57
43 John Lackey 5.6 5.71
44 Gio Gonzalez 5.55 5.53
45 Lance Lynn 5.55 2.68
46 Eric Stults 5.5 7.09
47 Felix Hernandez 5.49 4.41
48 Zack Greinke 5.48 2.03
49 Hisashi Iwakuma 5.47 3.28
50 Jose Quintana 5.46 4.5
51 Ian Kennedy 5.46 8.95
52 Ricky Nolasco 5.45 7.23
53 R.A. Dickey 5.44 6.42
54 Jeremy Hellickson 5.4 3.1
55 Homer Bailey 5.38 3.44
56 Miguel Gonzalez 5.36 9.47
57 Madison Bumgarner 5.34 5.37
58 James Shields 5.32 1.58
59 Adam Wainwright 5.32 2.99
60 Bartolo Colon 5.32 3.79
61 Derek Holland 5.3 7.61
62 Kyle Lohse 5.26 3.63
63 Cole Hamels 5.18 4.91
64 Anibal Sanchez 5.18 3.96
65 David Price 5.18 8.7
66 Chris Sale 5.14 6.73
67 Justin Verlander 5.06 8.25
68 Chris Tillman 5.04 1.75
69 Jose Fernandez 5.03 5.23
70 Shelby Miller 4.98 6.24
71 Matt Cain 4.97 2.93
72 Clayton Kershaw 4.9 5.34
73 Julio Teheran 4.9 2.92
74 Matt Harvey 4.86 1.01
75 Cliff Lee 4.79 4.86
76 Travis Wood 4.78 3.6
77 Dan Haren 4.78 4.26
78 Yu Darvish 4.53 1.72
79 A.J. Griffin 4.46 5.4
80 Mike Minor 4.46 5.29
81 Max Scherzer 4.15 3.36
– – – –

 

Some notes:

  • Groundballs are still good, they’re just not as good.
  • A combination of groundballs and contact lead to more unearned runs. The pitchers at the top of the board demonstrate this.
  • A combination of strikeouts and fly balls will tend to limit the impact of unearned runs, as demonstrated by the bottom of the board.
  • Errors that occur on fly balls tend to be more costly than errors on ground balls. This metric accounts for that gap, but the low likelihood of fly-ball errors make this bullet point’s effect relatively negligible.
  • Line drives are similar to fly ball in terms of error rate, but they tend to be less costly than fly ball errors.

I’m sure there is more to be gleaned, but the point is this: we need to stop trying to predict ERA, because ERA is not a pure value stat. We should be trying to figure out how many runs a pitcher should/should have given up, because that’s what matters. Runs matter, and who cares if they’re unearned? They’re kind of the pitcher’s fault, anyways.


What Is an Ace? (2013)

by
December 24, 2013

After the 2011 season I asked, and attempted to answer, the question, “what is an ace”?

It’s time to do that again.

Kershaw

Ok. While Kershaw is the aciest of aces right now, that’s not really the answer that we’re looking for.

I certainly don’t claim to be the first person to do something like this, nor am I the most rigorous, but I think it’s good to take a look at things like this every now and then just to reset our baselines.

What I did was to take the average of every starter’s fWAR and RA-9 WAR. Then I used that number to group pitchers into groups of (roughly) 30 — 30 aces, 30 number 2’s, etc. Then, I looked at the average performance of the pitchers in each group.

Here’s what I found:

There’s a couple of interesting things to note.

One is that the best 30 pitchers in baseball are, far and away, the best group. They strike out the most hitters, they walk the fewest hitters, they give up the fewest home runs, they have the lowest BABIP, they’re the best. That’s not surprising when guys like the above-pictured Kershaw, Cliff Lee, Max Scherzer, Justin Verlander, Matt Harvey and Yu Darvish are in the ranks.

The second interesting thing is how similar the #3, #4 and #5 groups are in terms of performance. Look:

#3 18.2% K, 7.2% BB, 3.85 ERA, 4.06 FIP, 4.04 xFIP, 4.13 SIERA
#4 18.7% K, 8.2% BB, 3.89 ERA, 3.86 FIP, 3.96 xFIP, 4.09 SIERA
#5 17.4% K, 6.9% BB, 4.26 ERA, 4.09 FIP, 4.02 xFIP, 4.12 SIERA

In many ways, every way other than walks really, #4 starters outperformed #3 starters. Well, in every way except for number of starts and innings. Number-three starters made about seven more starts and pitched almost 50 more innings than #4 starters. Similarly, #5 starters were a little worse than both #3 and #4 starters but what really limited them from producing value was that they made 12 fewer starts and pitched half as many innings as #3 starters.

The third point is similar to the above. Starters not in the top five accounted for more starts and more innings than the best pitchers in baseball. That makes sense when you stop to think about it, there are more bad pitchers than elite ones, but we don’t think about just how important it is for the other starters to make their starts so these guys don’t have to.

As I mentioned when I first did this little exercise after the 2010 season:

Next time your team signs a pitcher with a 10 – 8 record and 3.99 ERA in 160 innings realize just what you are getting. One of the top 100 pitchers in the league.

The numbers are a little different now — now the average #3 is 10 – 9 with a 3.85 ERA in 158 innings — but the point remains the same: the average baseball fan vastly underrates pitcher performance.


« Previous Page — « Previous entries
Next entries » — Next Page »