If you missed the first part and want a little more explanation about what I am doing click here.  I am going to start getting into the meat today with larger sample sizes and more typical groups of players.

Age 21 cohort:

There were 102 players in this group, three played only 1 season and were removed.  This is not as necessary with this group, but it becomes pretty important in the later cohorts as you will see.  The main thing is that for the max % part it is automatically 100% for the first year for any player with only one full season.  The 99 players left have an average number of 10.3 full seasons in the majors, so less than the previous cohorts as expected but still long careers on average.  There were 10 players that posted their max wRC+ in that first full season, and 9 posted their max WAR.  Said another way, about 90% of the players went on to have their best season later in their careers making it unlikely that a 21 year-old reaching the 300 PA plateau minimum is showing you a career year.  Again, part of this is that they on average have 9+ seasons to go so they have a lot of opportunities to have better years which the older cohorts will not have.

We also start to see something else I was expecting.  The players who max out in their first year tend to have shorter careers because they are not as good of players on average and that first year max was not very high.  Those that maxed wRC+ averaged only slightly over 4 years of 300+ PAs, and the ones that maxed WAR were only 3.25 years on average (with one active player in the group.  There is some overlap, but the two groups are different and will be for every cohort.  It is likely the trend here continues as well.  If you max WAR your first season it means you are not showing overall improvement later and leave the league quickly.  Those that max wRC+ but not WAR are likely getting more playing time later due to defense or other peripheral skills that are making them better players overall.  On to the max % chart:

It looks like there is some slight improvement in the first couple of years in hitting.  The increase is more drastic in WAR, partly because those that stick in the majors get more playing time and thus accumulate more WAR, but the increase might be more than that especially if the slight uptick in hitting is for real, though I will spend more time trying to tease that out after I have this base run through all the cohorts done.  You will notice that these players peak younger than our traditional understanding of peaks.  The group peak is around 24 and hitting stays around that level until their early 30s, but the WAR starts dropping the next season.

Age 22 cohort:

This group started with 200 players of which 41 only played 1 season and were removed.  The one season group in this case held a lot of current young players such as Wil Myers and Yasiel Puig, so this might be an interesting group to follow over the coming years.  The average tenure of the remaining 159 players was 8.6 full seasons.  Of those 159, 27 had their best wRC+ in their first season and 26 had their best WAR.  Now instead of 90% having better seasons later in their careers, we are down to 83 or 84%.  About one out of every six 22 year-olds never improve on their first full season.  The average number of full seasons for those that did max in year 1 was 4 years for both wRC+ max and the WAR max group with the second being only a few hundredths of years below the first.

The chart shows a less distinct increase in the first few seasons, but is upward sloping for both wRC+ and WAR until the age 26 season.  There is a similar decline pattern to the 21 year-old group.  The 21 cohort just had a steeper early incline and younger peak.

Age 23 cohort:

Now we start getting into the largest cohorts.  The most likely time for a player to get their first full season is from ages 23 through 25, and if you haven’t made it by then your odds as a player of ever getting a full season in the majors start to drop off.  This age group started with 320 players total and 43 were removed as one year players like before 7 of which are active players.  Of the 277 left they average number of full seasons played was 7.6 and now 56 had max wRC+ in year 1 and 52 a max WAR.  That is nearing the mark where a full quarter of the players are never better than their first full season.  Of those that maxed in year 1, the wRC+ group had an average of 4.3 full seasons and the WAR group was 3.9 years.  Frank Thomas was in the max WAR group, so despite playing 14 more seasons above the 300+ PA  level after 1991 (only 240 PAs in 1990) he never posted a higher WAR.  He had 2 seasons where is wRC+ were equal or greater than that first one, but didn’t amass enough PAs to accumulate more WAR, though in 1997 he tied the WAR and wRC+ of that first full season.  Anyway, chart time:

It’s harder to see much of any improvement in hitting with this group. There might be a slight improvement peaking in the 26 season again.  WAR shows an increase that is fairly steady until age 27 and then another similar decline phase.  Another thing to note, the hitting % of peak average at its peak is consistently in the low 80%.  For WAR it is declining so far.  If you look at the WAR line on the three charts, the first hits a peak of 60.3%, the second at 56.4%, and the third at 55.8% and might be worth keeping an eye on as we go on to the next set of cohorts.  For now though I will wrap it up rather than going on for the 3 or 4 thousand words all of the cohorts and summaries might take.

 Two roads diverged in a wood, and I–

I took the one less traveled by,

And that has made all the difference.

— Robert Frost

There are many things that stand out about this year’s Oakland A’s. Their incredible run differential has reached a near historic level, their breakout star from last year has proven that last season was no fluke, and the top three starters are pitching at incredible levels. They’ve been marauding through the American League like Heisenberg’s nemesis through Janjira. However, there’s one aspect of this team that flies under the radar: of their current 25-man roster, only two players were acquired through the amateur draft – Sonny Gray and Sean Doolittle. The rest were acquired through a mix of trades, free agency, waiver claims, purchases, and even one conditional deal.

Billy Beane made his name a while ago by not being afraid to stray from the pack, and in fact looking for those market inefficiencies that could save him a buck or two with the low payroll A’s. By trading for players who may have disappointed at other spots across Major League Baseball, or claiming players put on waivers, Beane is once again finding talent in the most frugal way possible. So is this a new phenomenon in Oakland? Let’s see what the numbers say. Here’s the acquisitional (who says you can’t invent words?!) breakdown of the Oakland A’s roster the last thirteen years.* This includes any hitters who made at least 100 plate appearances and any pitchers who pitched in at least ten games in addition to this year’s current 25-man roster.

* Why thirteen years? Because, Moneyball, of course!

AD*= Players acquired through amateur draft;  FA**= Players acquired through free agency;  T***= Players acquired through trades;  AFA^= Players acquired through amatuer free agency;  WC^^= Players acquired through waiver claims;  P^^^= Players acquired through purchases;  CD’= Players acquired through conditional deals;  R5’’= Players acquired through the rule 5 draft;  MnD’’’= Players acquired through minor league draft

While the A’s have always built their roster through trades more than through the draft (the only years those numbers were even tied was in 2007 and 2003; every other year there were more players acquired via trade than draft), the trend is becoming more and more evident as of late. On the A’s current 25-man roster, there are a measly two players who the A’s acquired through the amateur draft versus sixteen acquired through trades. Granted, the number acquired through the draft was bound to be a bit smaller so far this season than in previous years since a 25-man roster was used this season, instead of qualified players (again, players who had either 100 plate appearances or ten games in which a player pitched in that given season), which totaled between 27 and 37 in the previous twelve seasons. However, given that the season with the second lowest number of players acquired via the draft was last season, there definitely appears to be a trend here.

Now the question becomes, “how does this compare to the league as a whole?”

Usually Beane is at the forefront of certain trends, so if the A’s roster composition varies greatly from the rest of the league, could it be the start of a league wide trend, especially given the A’s incredible success so far? To answer that question, data on all 30 teams’ roster composition was collected for the 2013 season. Given the same requirements as the previous A’s seasons (100 plate appearances or ten games pitched), how did other rosters across Major League Baseball look last year?

That’s a lot of numbers, so let’s take a step back and look at some of the numbers that stick out. First of all, instead of using raw totals, percentages have been used to even out the variance among how many players each team had qualify for this roster construction study. It’s also important to note that the highest and lowest percentage in each column has been bolded (this was used only for the three primary ways of acquiring players – the amateur draft, free agency, and trades). One may think of the old adage, “there’s more than one way to skin a cat” when looking at the top of the league. Apparently this adage holds true for baseball roster construction, as well as cat mutilation, as the St. Louis Cardinals – you know, that franchise that has won four of the last ten NL pennants with a pair of titles, and has the self-proclaimed best fanbase in baseball – has gone the complete opposite direction as the A’s to build their squad, relying more on the amateur draft than any other team in baseball, and doing so with great success. Then there are last year’s World Series champions, the Boston Red Sox, who were among the league leaders in players brought in through free agency.

One consistent, league-wide trend was that teams at the bottom of the league standings had far more players qualify for the 100 plate appearance/ten games pitched minimums. This is a bit of a “chicken or the egg” type observation, where the cause can sometimes be confused with the effect. There are several teams among the league’s cellar dwellers that went through numerous players throughout the season in an attempt to find effective players (the “throw the spaghetti at the wall and see what sticks” approach Jonah Keri has referenced on multiple occasions). This would be your Marlins, Astros, and Cubs. However, there are also teams among the lower tier of the standings that were forced into more personnel choices due to injuries; your Phillies, Blue Jays, and Angels. Whatever the reason, it is noticeable that nearly all the teams at the top of the standings at the end of the year have fewer players qualified for the 100 plate appearance/ten games pitched minimums thanks to good health and a clear vision – two staples of successful franchises (interestingly enough the one team that was an exception to this rule in 2013 was the Boston Red Sox; however, given their disaster of a 2012 season, it’s not as surprising to see that they tinkered a bit with their roster throughout the season).

The data supports what many baseball fans would already think, which is that the teams with higher payrolls usually are among the most reliant on free agents, and, in order to compete, the smaller market teams need to find other ways to build their rosters. For example, the top eight teams who built through free agency were: the Cubs, the Tigers, the Phillies, the Giants, the Brewers, the Yankees, the Red Sox, and the Dodgers. Of those eight, the Tigers, Philles, Giants, Yankees, Red Sox, and Dodgers make up the top six teams by payroll in 2014. The Cubs are in the middle of a complete roster overhaul, and Theo Epstein seems to be constructing a team built for flipping at the deadline for future prospects, so cheap free agents are a prime commodity. The Brewers are the odd team out, and would make for an interesting case study.

On the flip side, the top nine teams created by trading players were: the Indians, the A’s, the Blue Jays, the Diamondbacks, the Pirates, the Rays, the Astros, the Padres, and the Marlins. Of those nine, the A’s Pirates, Rays, Astros, Padres, and Marlins made up the six lowest teams by payroll in 2013; the Indians were not far off, with only the 21^st biggest payroll of 2013; and the Blue Jays and Diamondbacks both have super aggressive front offices that prefer to bring in players via (usually poor) trades.

There is, of course, the caveat that while this study looks at general roster construction it does not have the nuance to differentiate between a team that is loaded with free agents that are big money free agents (like the Yankees and Red Sox) versus a team loaded with replacement level free agents (like the Cubs). If each player’s salary was totaled by how he was acquired, and then turned into percentages of roster construction again, this would show us how much each team is truly investing into each method of roster construction from a financial point of view. This could be used to compliment Jonah Keri and Neil Payne’s recent study that looked at roster construction. In their piece, Keri and Payne look at roster construction through the lens of a stars and scrubs roster versus a balanced roster. Although there might be some discrepancy based on the arbitrary 100 plate appearance and ten games pitched cut-offs, the data likely wouldn’t be vastly skewed from the current results.

Todd Boss, of Nationals Arm Race did an interesting study somewhat similar to this one, looking at the core players (the 5-man starting rotation, the setup and closer, the 8 out-field players, and the DH for AL teams) for the playoffs teams in 2013, and put the teams into four different categories of roster construction: draft/development, trade major leaguers, trade prospects, and free agency. The results were similar to what was found here, and help to support the idea that the arbitrary cut-offs of 100 plate appearances and 10 games pitched didn’t have a negative impact on the study. The only slightly different result was that Boss found the Rays to be relying more on the draft than on trades.

Having looked at the league-wide breakdown for roster construction last season, let’s take a look at roster construction from an historical perspective. To make a long story short, when Curt Flood took on Major League Baseball, and eventually the Supreme Court, in his fight to turn down a trade to Philadelphia (who can blame him?), he opened up the Floodgates (couldn’t help myself) for the eventual implementation of free agency in baseball. So, has successful (being judged by the extremely arbitrary “ringz” perspective) roster construction changed since then? Let’s take a look with yet another chart (Marshall Eriksen would be proud), this time looking at the past 40 World Series winners, and how each team was constructed.

#DC+= Players acquired through free agent draft compensation;  #XD++= Players acquired through the expansion draft

The first note that needs to be made is regarding the 1997 Marlins and 2001 Diamondbacks. Both rosters had skewed roster construction due to how soon after the team’s inception they were able to win a championship. The Marlins have by far the lowest reliance on the amateur draft, and the Diamondbacks have tied for the highest reliance on free agents, but both of these numbers were driven up (or down) by the limited time for drafting and moving along prospects before their championships.

After accounting for the 2001 Diamondbacks season, the steady rise of reliance on free agents since the mid-seventies is notable – up until three years ago that is. It’s hard to tell whether baseball is undergoing an actual “grass roots” movement, with teams relying less and less on big market free agents to succeed, or if this is simply a three-year blip in the radar, but it is certainly notable that the last three World Series winners have had notably lower reliance on free agents than the previous seven years’ winners. The 2011 Cardinals, 2012 Giants, and 2013 Red Sox have not, however, relied on trades, but instead their farm systems more so than other winners of this millennium (not including the 2002 Angels).

In fact, excluding the fluky 2003 Marlins, there has not been a World Series winner as reliant on trades as the 2013 A’s (50 percent) since the mid-eighties Twins and Mets. What’s even more troubling for the A’s is that there hasn’t been a team to use the draft and free agency combined as little as the 2013 A’s since the 1982 Cardinals, a team built during the dawn of free agency.

When judging by championships, in fact, the picture of baseball as a sport in which you need to be in a big market, with the ability to sign big name free agents becomes unfortunately evident. The roster composition of nearly all of the World Series winners this century is quite similar to that first group of teams mentioned above as big market teams built through free agency. This is no surprise to any real baseball fans, however. Look at the cities that have hosted World Series parades since the Yankees’ dynasty of the nineties began. Sure, there are the success stories in Florida and Arizona, but other than that it’s a who’s who of big market teams. While the Cardinals play themselves off as plucky little underdogs, their payroll was the eleventh largest in baseball last year, almost exactly twice that of the A’s.

That’s why this year’s A’s team could be so special. If they are able to continue their regular season success, and finally make the breakthrough they have been struggling so much to make in recent years, they could continue the recent trend of teams moving away from a strictly free agent diet to fulfill their championship dreams. Of course, this has been the case for a couple of years in Oakland now, and it hasn’t happened yet. However, with the top three in the A’s rotation looking as good as any in baseball right now, baseball’s secret superstar at third, and the fact that it is the 25^th anniversary of the last A’s World Series title, suddenly it doesn’t seem that unlikely that the A’s could make ole Bobby Frost proud this October.

Before the 2012 season, some folks drafted J.D. Martinez as a deep sleeper, coming off a decent debut with the Astros in 2011 and a solid minor league profile. He went on to slug only 11 HR in 439 PA and hit a disappointing .241/.311/.375.  What went wrong? Well, he pounded the ball into the ground at a 51.8 % clip. His line drive % dropped to 16.6 % and he hit only 31.6 % flyballs. It’s hard to hit HR’s and hit for average with that kind of batted ball profile.

He got demoted to AA after failing to impress in 2013 and got injured. This year, for the Tigers, he mashed in AAA, was called up in late April, and has already hit 7 HR’s in only 117 PA with a .312/.342/.596 batting line. So what has changed? Read the rest of this entry »

In baseball, part of what is commonly debated is how important it is to hit with runners in scoring position. Viewers of their teams will often have their sad sigh when their team leaves runners stranded in scoring position and will look up how their team does in those situations and say, “this is why we don’t score runs” or “this is why we don’t win games.” They will also look at other teams and see how good of an offense the other team might have and immediately make the assumption that they are going to be better at hitting with runners in scoring position than most other teams if their offense is better. But just how much of a team’s success is based on hitting with runners in scoring position and how much of hitting with runners in scoring position is based on team success?

I. Impact of Hitting with Runners in Scoring Position

One of the old clichés in baseball is, “you can’t win without hitting with runners in scoring position.” Many people link that to why the Cardinals had done so well in the past and why they haven’t really been able to get going this year. In years past, they have consistently been not only one of the best teams in baseball, but also the best at hitting with runners in scoring position.

Many people in the game consider it also to be one of the most important stats when it comes to judging a player’s hitting ability. In a press conference at the beginning of the season, Matt Williams had sabermetricians finally thinking that someone with their ideology was becoming the manager of the Washington Nationals when he said, “If you don’t get with the times, bro, you better step aside.” When I heard that, I immediately thought that he would be talking about more advanced hitting metrics than batting average and home runs and RBI’s. He followed that comment up with, “My favorite stat right now and always has been the stat of hitting with runners in scoring position. Because batting average and on-base percentage and all of those things are great, but who is doing damage and how can they hit with guys in scoring position.” When I heard that, I immediately slunked back in my chair and placed him in the category of old-school.

And listening to one of the Reds games (as I always do), listening to Marty Brennaman (who I think is a good broadcaster for his catchy phrases and also because he’s from where I’m from), I heard him talk about Votto and he said, “Votto will take a 3-0 pitch an inch off the outside corner, when he could do with it what he did Wednesday. I believe in expanding your strike zone when you’ve got guys on base.” For those who don’t know, what he did on Wednesday (a while ago), was drive a 3-0 pitch from Matt Harvey (that shows how long ago it was) for a home run to left field in New York. Unfortunately, for a while now Marty Brennaman has been seemingly leading a war of the old-school against his own team’s star first baseman Joey Votto over hitting. Namely hitting with runners in scoring position or men on base. Again, while listening, I slide back in my chair, disappointed in Marty for being so illusioned and confused and broadcasting his wrong opinion to many of the people who listen to him on the radio.

Williams and Brennaman aren’t the only people that have this mindset though. The thing that they and many other people think is that if you can’t hit with runners in scoring position, you can’t win games and you can’t score runs. For these people, it is for the most part a blind hypothesis, just assuming it is true because it seems that it should be true.

For examining this data, I am going to look at the coefficient of determination, or R2 (I have below this the formula for R, correlation coefficient, that when squared equals the coefficient of determination). For those who don’t know, when looking at the data and calculating a formula of best fit, R2 shows a percentage value of how many of the samples of the x-value fit the line of best fit (the line that in perfect situations can calculate the y-values). I am going to call the dependent variable, or y-value, wins and runs and the independent variable, or x-value, the various offensive statistics that I will use to test my hypothesis (hitting with runners in scoring position does not have much to do with determining how many wins a team gets in a season or how many runs a team scores). Basically it is how dependent team wins and runs are on hitting with runners in scoring position. Before I look at hitting with runners in scoring position, it is important to establish which three offensive statistics are the best at determining wins and runs.

In terms of influencing the scoring of runs from 2002 to 2013, the three best offensive statistics are:

1. OPS with an R2 of .9132 (91% of the OPS x-values fit the formula: y = 2059.2x – 791.27)
2. ISO with an R2 of .5801 (58% of the ISO x-values fit the formula: y = 3279.75x + 238.02)
3. wOBA with an R2 of .3999 (40% of the wOBA x-values fit the formula: y = 3482.9x – 389.93).

When it comes to which statistics determine wins the most, the three best statistics are:

1. WAR with an R2 of .5329 (53% of the WAR x-values fit the formula: y = 1.1243x + 59.614)
2. wRC+ with an R2 of .4302 (43% of the wRC+ x-values fit the formula: y = 0.8977x – 5.4636)
3. wRAA with an R2 of .3632 (36% of the wRAA x-values fit the formula: y = 0.1033x + 81.239)

There are a couple things to notice when looking at this data. One of those things is that most offensive statistics have a much weaker coefficient of determination when looking at wins, largely in part to the fact that pitching is kept completely out of the equation. Another thing to know is that if there was a bigger sample size, the R2 values would be different but using this sample size (which I will use for RISP), these are the R2 values that show up.

The purpose behind collecting those statistics in terms of offense in general as opposed to just RISP is because this way there will be statistics to use when looking at how much RISP influences offense. Looking at determining runs scored in an overall season with RISP numbers:

1. OPS has an R2 of .3099 (31% of the OPS x-values fit the formula: y = 948.7x + 19.173)
2. ISO has an R2 of .2395 (24% of the ISO x-values fit the formula: y = 1812.2x + 470.92)
3. wOBA has an R2 of .2898 (29% of the wOBA x-values fit the formula: y = 2391.5x – 35.754)

It is quite a dramatic change, especially when looking at OPS that clearly had a big hand in determining runs scored in a season. While some of them still have some modest effect in determining runs scored, it is still not quite at the same level as those that covered a full season and not just a given scenario. Now looking at how those other statistics determine wins with runners in scoring position:

1. WAR has an R2 of .29 (29% of the WAR x-values fit the formula: y = 2.5609x + 68.94)
2. wRC+ has an R2 of .2739 (27% of the wRC+ x-values fit the formula: y = 0.5518x + 27.727)
3. wRAA has an R2 of .2366 (24% of the wRAA x-values fit the formula: y = 0.2366x + 80.996)

As I had mentioned before, it should be expected that these numbers ought to be low because there is much more that goes into a win than just offensive ability. There has to be great pitching too that is not put into account. With that said, these numbers are quite far from being great in determining wins as is evidenced by their still being far away from even the 50% mark that they should be close to.

For Matt Williams’ sake, I also looked at how much batting average with runners in scoring position determines wins and runs:

1. For scoring runs, AVG has R2 value of .181 (18% of AVG x-values fit the formula: y = 2005.8x + 213.05)
2. For wins, AVG has R2 of .1427 (14% of AVG x-values fit the formula: y = 257.76x + 13.255)

So Matt, not to rain on your parade, but batting average with runners in scoring position has very little to do with determining runs or wins. And Marty, it’s just limiting Votto’s overall production to a small sample size that doesn’t have a whole lot to do with winning games. No one will argue that hitting with runners in scoring position can help to win games because it does often result in scoring a run but it should not be looked at as one of the key stats in a player’s production.
II. Is it dependent on overall strength of offense?

Now back to those St. Louis Cardinals. Last year, with runners in scoring position, they put up not only unreal numbers, they put up numbers that are really just plain stupid. I mean, they batted .330 with runners in scoring position, had a .370 wOBA, and a 138 wRC+, and won 97 games, 32 games over .500. Like I have previously established, those numbers are intrinsically worthless considering that it is such a small sample size but those are still just gaudy numbers. This year, for lack of a better word, they’re awful with runners in scoring position. A .244 batting average, .293 wOBA, and 86 wRC+ all those with runners on second or third and have won 39 games, only 4 over .500.

Many people look at that and think that clearly, their inability to hit with runners in scoring position this year has caused the drop off in production. Of course, the low .303 wOBA, 92 wRC+, OPS of .681, and AVG of .250 are a bit of a drop off from the .322 wOBA, 106 wRC+, .733 OPS, and .269 AVG of last year might have something to do with that drop off in offense too. The Cardinals offense is also scoring about a run less this year than they did last year (4.83 Runs/9 innings in 2013 and 3.67 Runs/9 innings in 2014) meanwhile their pitching has practically been identical to last year with a FIP of 3.31, xFIP of 3.66, and SIERA of 3.60 this season compared to last year’s 3.39 FIP, 3.63 xFIP, and SIERA of 3.57. But is hitting with runners in scoring position dependent on how the offense overall is? I’m sure you can already see what coefficient we’re going back to.

The process was similar to last time, with the dependent variable, or y-value, being hitting with runners in scoring position, and the independent variable, or x-value, being the same statistic only looking at the value over the course of a full season. I found that wRC in a year has by far the strongest effect in determining how a team hits with RISP with an R2 of .7527 with 75% of the x-values fitting into the equation of y = 0.3364x – 51.232. OPS is after that with an R2 of .6487 and 65% of the x-values fitting the equation of y = 1.0184x + 0.0025. And then there is wOBA that has an R2 of .6258 and 63% of the x-values fitting the equation of y = 0.9807x + 0.0062. Some other values are:

• wRAA that has an R2 of .5811 (58% of the x-values fit into the equation: y = 0.2586 + 0.5721)
• wRC+ that has an R2 of .5558 (56% of the x-values fit into the equation: y = 0.9678x + 3.3038)
• WAR that has an R2 of .3831 (38% of the x-values fit into the equation: y = 0.2005x + 0.8901)

So a case could be made that the strength of a team’s offense overall does dictate how that same team hits with runners in scoring position. While by no means is it an overwhelmingly strong coefficient of determination in any of the cases, in most cases the strength of an offense determines at least 50% of hitting with runners in scoring position which is good enough to at the very least say that better offensive teams are more likely to hit better with runners in scoring position than weak offensive teams.

Ever since I read Jeff Zimmerman’s aging curve article in December I have been thinking more about aging curves in general.  That has lead me to take a step back and start digging through players in a different way.  Jeff gave a couple of plausible reasons for the difference in aging curve, teams are developing players better prior to appearing in the majors and that they are doing a better job of identifying when they are ready.  I’ll throw another out there before I start this.  MLB has gotten younger recently and to do that you need to be pulling in more young players.  In general you would expect players first pulled up at each age point are in the farthest region of the right tail of the talent distribution and then you move left as you add more players from that group.  Maybe a larger percentage of the younger players being brought up just are not as good and won’t ever thrive at the big league level.  Anyway, let’s get to what I have started working on to see if breaking things apart can shed any light on the subject.

To start I pulled every position player year for rookies in the expansion era (after 1960) and ended up with 2,054 players and 11,585 player seasons including active players not just completed careers.  Then I broke players into age cohorts with when they played their first season with at least 300 plate appearances which I will refer to as full seasons the rest of the way.  I will be working through to see if players age differently based on what age they reach the majors and get regular playing time.  To do this I will mostly be looking at percent of peak wRC+ and WAR.  For this post I am only doing the first couple of cohorts and then I will work through more in the coming weeks.

The first cohort I broke down was the age 19 group.  Only one player amassed the 300 plate appearances necessary at age 18, Robin Yount, so there is not much to learn there except that if you can hack it at the big leagues when you are 18 you are probably really, really good.  That will be true for the 19 and 20 year-olds as well, but there are more of them.  The age 19 cohort is also small with only 8 players; Ken Griffey Jr., Edgar Renteria, Bryce Harper, Cesar Cedeno, Tony Conigliaro, Ed Kranepool, Jose Oquendo, and Rusty Staub.  This will be the only cohort small enough that I will list everybody.  Interestingly the age 20 cohort has a lot more star power as Griffey is the only Hall of Famer (I know he isn’t in yet, but he will be on the first ballot).

Of the seven 19 year-olds that have retired, the average number of full seasons played is almost 13, so they did have long careers as you would expect.    None of the players peaked in wRC+ or WAR in their first full season, which is not surprising.  The more seasons you are in the majors, the lower the probability that the first season will be the best one just because you have more opportunities to best it.  Harper actually put up a better wRC+ in year 2, though his rookie WAR was better and this year isn’t looking like a new high for him so far.  If you take their average percent of peak at each age and chart it this is what you get:

The sample size here is so small I wouldn’t want to believe it too much, but we might see some improvement for this cohort early in their careers.  The peak, if there is one, looks like 25 to about 27 especially in WAR.  Then it is all decline.  Again, these are players from the ERA that showed this before, not from players in the last 10 years that are not showing improvement in Jeff’s article.

Let’s move on to a bigger group and see what happens.  The age 20 cohort includes 37 players with 10 current players.  There are Hall of Fame or near HoF players all over.  Rickey Henderson, Roberto Alomar, Ivan Rodriguez, and Johnny Bench are in along with Alex Rodriguez, Joe Torre, Andruw Jones, Gary Sheffield, Alan Trammel, Adrian Beltre, and Miguel Cabrera.  Mike Trout  is the only young guy I would assume has to eventually make it, but there are a couple others there that might eventually be that good too.  In my opinion, about a third of this group are HoF caliber or will be after their career is done.  That is 1 out of every 3 players that stick in the bigs at age 20 will be good enough to make it to Cooperstown.  Way better than the 19 year olds.  The average career length for those that are not active was over 11 years, so again most should not max out in their first year.

Only three players had their best hitting season as a rookie, but it was because all three of them had their only 300+ plate appearance season at age 20 so it was the only season in the sample.  Danny Ainge was one of the three though, so we could go see when his basketball career peaked instead maybe.  All three therefore also had their best WAR season at 20, but there was a fourth player who had his max WAR in that first full season, Claudell Washington.  Washington had 14 full seasons as a major leaguer and his best by WAR was year 1, and he had only one wRC+ better than that first year.  If we look at the chart for the age 20 cohort chart it looks way different than the 19 cohort.

Again, this is not a large sample, and it is overwhelmed by extremely good players.  There seems to be an increase in the first couple of seasons followed by a long, flat peak that for wRC+ goes all the way into their early 30s.  WAR is more volatile and might start declining a couple of years sooner.

I expect that this will get more informative as we get into more normal players and larger samples, but it is fun to look at elite players.  I’ll break down a couple of more age groups in the near future, and eventually try and build a regressed model for the bigger cohorts to control for the era and some of the other effects that aren’t rolled into wRC+ or WAR.

There are many arguments against the sacrifice bunt, by many sabermetricians and sports writers, all with the purpose of retiring its practice in baseball. The three main reasons not to bunt are that it gives away an out (out of only 27), the rate of scoring goes down (based on ERT by Tango), and that most bunters are unsuccessful.

For my argument, I will establish a more romantic approach and one I haven’t seen across the world of sabermetrics. With this approach, I will land on a conclusion that supports the sacrifice bunt and even speaks to the expansion of its practice.

Bunters can be successful

First, I’ll attack the last argument. If bunting is coached, bunters will be better. In my own research, as well as research done by others, I’ve found that there have been years when even the pitchers are able to bunt successfully over 90% of the time. Many people say that practice makes perfect, and while perfection might not be reached in the batters box, I wouldn’t be surprised if bunters were allowed to get close, or at least to their abilities in the 80’s.

Innings are more prosperous after bunt

The second argument is the main staple of this essay. In the world of analytics, general numbers are not good enough to explain why a phenomena is bad. Tom Tango’s famous Run Expectancy Matrix is used to make arguments against bunting across the Internet. Unfortunately, it’s assumed that the situations just exist rather than being set up the way that they are. It would be appropriate to use the table if a team were allowed to place a man, or men, on a base, or bases, and set the number of outs. However, as a strong believer in the principle of sufficient reason, I believe that there’s variability between a man on second with one out from a bunt and a man on second with one out from other situations.

For this reason, I set up my own analysis through the resource of Retrosheet play by play for the years of 2010-2013. To make things simple and not delve too deeply in varying circumstances, I will simply use larger data sets and noticeable differences to tell a story. First, I will look at only innings that start with men on base before the first out. Sacrifice bunts cannot happen when men are not on base, so it would be unfair to statistically compare innings with bunts to just innings without bunts. In line with Retrosheet’s system, I’m looking at all instances of SH, when they occur before (and usually result in) the first out.

To summarize, I’ll be looking at the percent chance that a team scores in an inning where they are able to get a man, or men, on base before the first out (as well as the average runs per inning when that situation is set up). I will compare this base situation to the percent chance that a team scores in an inning when they decide to sacrifice for that first out (as well as the average runs per inning when that situation is set up).

This data can be seen below with a total of about 53,000 innings across seasons where men were on base before the first out. In general, through the four years, teams score in about 26.8% of innings with about 0.478 runs per inning (RPI); when men get on base before the first out, they score 45.8% of innings with a .691 RPI. (In innings where a leadoff HR is hit, this does not count as men on base (nor will these runs count in calculation of either group, assuming men get on after the home run is hit, and before an out)).

Many managers, if not statisticians, understand this increase in the chance to score a run; after all, that’s why they do it. In 2010 and 2013, deciding to, and successfully laying down a sacrifice bunt resulted in a 13% increase in the ability to score that inning for the AL. And while it would make sense that the argument stops there, RPI also supports the sacrifice bunt (with data of the last four years). (Here, again, RPI = Runs scored after MOB B1O situation divided by number of innings of situation.)

This increase in RPI (seen as high as 0.137 Runs Per Inning larger than without bunting, 2012 AL) can contribute a decent number of runs over the course of a season. For example, in 2013, if the Oakland Athletics bunted a little less than once per series, they would have been on par with National League teams with number of bunts (in the 60’s). If they were able to bunt 47 more times (68, rather than 21), then their run total would have given them enough wins to have the best record in baseball (using Bill James adjusted pythagorean expected win percentage).

To summarize, an adjusted estimated runs table with respect to sacrifice bunt set up positioning and outs would produce more runs than the average table that does not take into concern how outs or players arrived at their position. This argument was suggested at the end of an essay by Dan Levitt, with earlier data in a more complex and subtle manner. RPI and the probability of scoring a run increase with a sacrifice bunt.

Bunting is symbolic of the greater good

The first and final argument to discuss is the idea that a sacrifice bunt throws away an out. In baseball, if a player bats out of order, or does not run out an error (among other mental mistakes), then that is giving away an out. And I believe that if a coach tells a player that he can’t hit, and to bunt because he can’t hit, then I wouldn’t argue that in those cases, you are giving away an out (knowingly removing the opportunity from the player to get a hit). So unless you believe that’s how coaches interact with their players prior to calling for the bunt, I will disagree with that notion.

The dictionary definition of sacrifice is “an act of giving up something valued for the sake of something else regarded as more important or worthy.” It’s the biggest theme in religious studies, the coolest way to die in movies, and the plot for heroic stories in the nightly news. Eliminating the psychological effects of a sacrifice, where they’re common place in our culture, seems slightly irresponsible after seeing the data.

This idea lends nicely to the discrepancy between American and National Leagues. Articles can be found, research has been done, and the common thought among those surrounding the game is that pitchers should bunt because they won’t do much else (in appropriate situations). In fact, an article by James Click gives the opinion that the lower the average, the more advantageous it is to bunt. However, my argument is the opposite. The amount they sacrifice, if they’re unable to hit is not valuable to those involved. If the pitcher is respected as a hitter, then their sacrifice is meaningful. Mentally as a leadoff man, if your pitcher is hitting sub .100, and there’s a man on base, he’s bunting because he cannot hit. That’s not a teamwork inspired motive, that’s a picking poison motive. The chart below shows data from the last four years when men get on base before the first out, it distinguishes that the National League is better than either league that doesn’t bunt, but far from as effective as AL bunters.

The argument can be made that the AL contains better hitters, and while I believe this, there would be a larger separation of the % scoring without bunting as well as the RPI of the innings where players get on before the first out.

Because of this separation, I feel that bunting is not giving away an out, but sacrificing for something greater. Simply put, if my teammate sets me up to knock in a run with a hit, that’s easier that having to find a gap, or doing something greater. In many cases, I might need to just find a hole in the infield. Also, I know that my team, and coach, believes in me to be successful. Professional athletes can’t possibly feel pressure and confidence that emanates from teammates with the hopes of greater success, that idea would be ridiculous, right? Those ideas are practiced and taught in business places and self-help books around the world.

Opposition

The data that I used was from Retrosheet, and while this data lists a lot of SH’s (sacrifice bunts) from where errors occur, to double plays, the main output is the standard sacrifice bunt. That being said, it does not include instances where the batter was bunting for a base hit (regardless of number of men on base), or other strange incidents of sacrifice failures (places where the scoring did not distinguish that an SH was in play). After recreating the analysis to include all bunts, the values of RPI and % scoring assuming men on base before the first out, values were still larger than without the bunt, but not as large as the sacrifice representation. This argument falls with the established idea that bunting could be more successful than most people think (especially when the bunt is a sacrifice). For instance, if the numbers above are reduced by as much as 85% in some cases, it still produces more successful results.

The next piece of opposition is that different circumstances have different weights in these situations, and that my case is too general to provide an advantage to a staff trying to decide whether to bunt. My argument is that upon analyzing circumstances, the most important element is the sacrifice bunt. In most situations, I feel that it will boost the team’s ability (and desire) to have success. With four years of data, my goal was to be able to refute the reliance on the simple Tango Run Expectancy Matrix, and how it is used, not to recreate one. In my opinion, in order for people to understand how historically successful situations have been, there should be hundreds of Run Expectancy Matrices highlighting how runners came to be where they are, as well as what batters follow.

The final piece of opposition has been created by myself during the generation of this essay or idea. The Heisenberg Uncertainty Principle relates to the ability to study the speed and position of a microscopic particle. Simply put, by studying one, you’re unable to observe the other. The act of observation limits the ability to fully observe. Because my argument is set up in a romantic sense, it could be argued that this principle relates. If coaches and teams start bunting every other inning, the act of giving oneself away for the greater good of the team will diminish and its advantage psychologically will wither away. In other words, the knowledge of how something effects one emotionally can limit one from being emotionally affected. I present this as an opposition because I feel that this might already be the case where if a pitcher is repeatedly bunting, teams will not think much of it as a quest for the greater good. However, when players are seen as an asset in the box, this advantage still exists; so teammates can still be sold on the relevance of the opportunity.

If these ideas spread, will this essay result in more bunts, especially when there are no outs? Probably not, because statisticians are stubborn. But it definitely provides an outlet for coaches who support the old school, traditional game of baseball.

Tip: Don’t understand an acronym? Just click on it and it will take you to the corresponding FanGraphs glossary of terms.

Watching the final game of the Yankees – A’s series last week, which featured one of the game’s finest pitchers in Masahiro Tanaka, I had a thought during Josh Donaldson’s final at-bat against the Japanese hurler. After he struck out to finish 0-3 against Tanaka, my mind traveled back to the ALDS game 5s of the past two years. It’s no secret the A’s crashed out against a dominant Verlander in both 2012 & 2013, just like it’s no secret that Josh Donaldson was almost entirely absent in both of those very important games: 1-7, 0 BB, 3 K (with all 3 of those Ks coming in 2013′s game 5). 7 at-bats is obviously an incredibly small sample size, especially for an up-and-coming player getting his first taste of the postseason. However, for what Donaldson means to the A’s, there were certainly quiet rumblings of disappointment among the fan base.

Verlander is very good; it seems he’s especially good in high leverage situations when his team needs him. Josh Donaldson is also very good, posting 7.7 WAR last year in 158 games. This year, Donaldson has been even better, posting 3.4 WAR through just 62 games and asserting himself in the conversation of the best overall players in baseball. A sizable portion of that WAR comes from the plus defense he plays, but his bat is what he’s known for: since getting called up from the minors on August 14th, 2012 (the point at which his consensus “breakout” started), he’s batted .291/.377/.509 with a wRC+ of 148 (which means that Donaldson has created 48% more runs than a league average player). Only one player has higher WAR in 2013 and 2014 combined (Mike Trout), and only nine other players have higher wRC+. Josh Donaldson is an elite defensive and offensive player by many metrics.

After watching Donaldson’s at-bats against Tanaka, I started wondering how he fares against other elite pitchers in the game, having an unproven hunch he might struggle against them. We know that most everyone struggles against elite pitching, as that is generally the very definition of elite pitching; however, there’s the larger question of just how much impact elite pitching has on hitting statistics, and how elite hitters fare against elite pitching. One might assume that elite hitters are better able to succeed against elite pitching. Looking at Donaldson’s statistics, you wouldn’t think that is the case.

Pulling data from the start of the 2013 season, I’ve identified some of the “elite” pitching that Donaldson has gone up against. I’ve tried to identify pitchers he has faced most often in terms of plate appearances – fortunately (for our sake at least), those pitchers he’s seen most often are also elite arms in his division, like Felix Hernandez, Yu Darvish, and Hisashi Iwakuma. All pitchers on this list are ranked in the top 15 for xFIP for 2013-2014 (minimum 160 innings pitched) with the exception of Verlander (77th) & Lester (41st). I’ve included them as their FIP rankings are in the top 40, and because I’ve already used Verlander as a benchmark above. Here are Donaldson’s statistics for 2013 & 2014 against some of the best arms in the game, with his total statistics overall in the final line for reference:

These figures don’t include the 2012 and 2013 postseason series against the Tigers, which actually helps Donaldson’s case. However, let’s get the small sample size disclaimer out of the way before we continue. 113 plate appearances is about a month’s worth of full-time hitting statistics, which is not a tremendous sample to draw from, but not insubstantial either. What’s clear from these numbers is that Donaldson really struggles against elite arms, posting awful strikeout and walk rates and severely depressed average, on base, and power numbers (just 7 extra base hits in 104 at-bats).

One larger question we have to answer is whether Donaldson’s drop in production vs. elite pitching is congruent with the standard drop of production any hitter would expect when going up against this level of competition. To find that out, I combined all of the batting-against statistics for these 12 pitchers for all of 2013 & 2014, a total of 12,534 plate appearances, which gives us a “league average” line vs. these pitchers. The findings? These elite arms are really good. Big surprise, right? In fact, the league strikeout and walk rates against these pitchers is very close to Donaldson’s rates, with the walk rate exactly the same. Here are Donaldson’s numbers vs. the elite pitchers, his overall numbers vs. all competition, and then the league average line vs. the elite arms:

Even though we’re looking at the best pitchers in baseball, these statistics were still a bit surprising to me, as these league-wide walk and strikeout rates are abysmal from a hitter’s perspective. How does Donaldson’s slash line compare to the league average? Again, let’s take a look:

We know that Donaldson’s poor BB and K rates fit tidily within the standards of the league line, as seen in the first graph, but his slash lines tell us that he’s been far worse than the rest of the league against these elite pitchers in the limited plate appearances we’re looking at. Shouldn’t we expect a player of his offensive caliber to fare better than league average against this level of competition?

The answer is not necessarily. Donaldson’s approach at the plate has a large bearing on the fact that he struggles against elite pitching. He is not a contact hitter, posting below average marks in swinging strike percentage, contact percentage, and Z-Contact percentage. In fact, he has changed his approach over the past calendar year specifically to try to hit more home runs, resulting in an almost 5% spike in his strikeout rate from 2013 to 2014 (16.5% to 21.1%), but also increasing his home run per fly ball rate by almost 7 points to 17.3%, an elite mark for someone who plays half of their games in one of the most pitching friendly ballparks in baseball. Coupled with an increase in his walk rate, Donaldson’s run creation output has benefited from Chili Davis’ hitting instruction, sitting on pitches he is more likely to drive and swinging hard at the expense of a lower average and higher strikeout rate. Donaldson batted .301 in 2013 with an inflated BABIP (.333), but with his change of approach, he projects somewhere in the .270 range moving forward.

Donaldson is the profile of a hitter that may be more apt to struggle against the elite pitching in the league due to the simple fact that elite pitchers tend to have makeups consisting of low walks and high strikeouts. For example, against “Power” pitchers (pitchers that are in the top third of the league in strikeouts plus walks), Donaldson has a career line of .210/.316/.356, showing that he struggles with pitchers who have strikeout potential, whether elite or not. He’s not alone in being a top offensive player that struggles against power pitching in relation to his overall performance: the benevolent baseball god Mike Trout slashes a fairly pedestrian (for him) .269/.379/.473 against the high strikeout arms.

The most important point to remember when looking at these statistics is that Josh Donaldson is currently one of the best players in baseball, regardless of his past performance versus elite pitching. He is a player that has enjoyed only a year and a half of sustained high-level performance and is continuing to make adjustments in hopes of greater success, which could completely alter his future at bats versus these elite arms I’ve highlighted. However, my gut tells me he may always struggle with these pitchers due to his approach at the plate, which trades contact for power – an Oakland A’s team-wide trait. It bears further scrutiny in the future for his potential playoff success, as he will obviously face more elite pitching in October when the average arms have gone home for the offseason. Will Donaldson and the Oakland A’s home run-centric approach carry them to a deep playoff run against the best arms in the game? Fortunately for us, it looks like we’re going to find out.

Wondering about the two home runs he hit off of Bumgarner and Sale? EXTRA CREDIT BONUS FREE BASEBALL GIFS!

Off Madison Bumgarner: May 27, 2013, 2-0, no out, 1 on, 4-seam fastball:

Off Chris Sale: June 8th, 2013, 1-1, 1 out, 3 on (oppo taco all the way), 2-seam fastball:

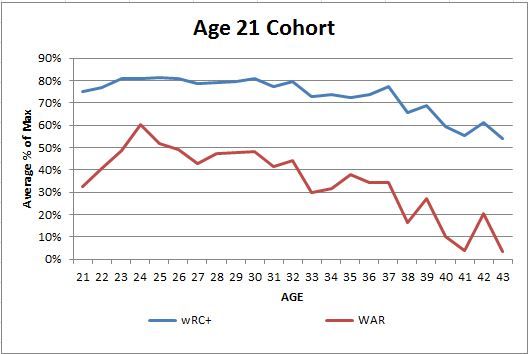
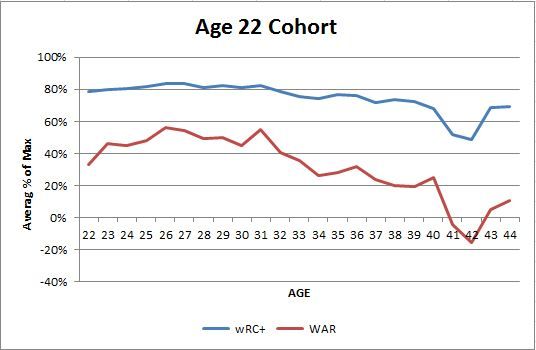
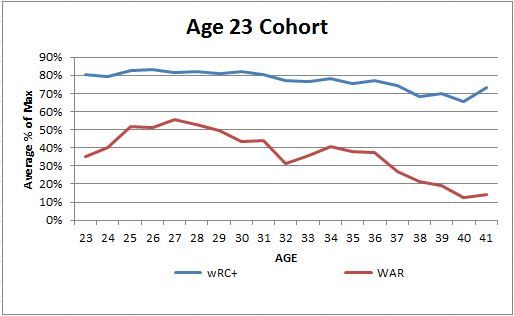
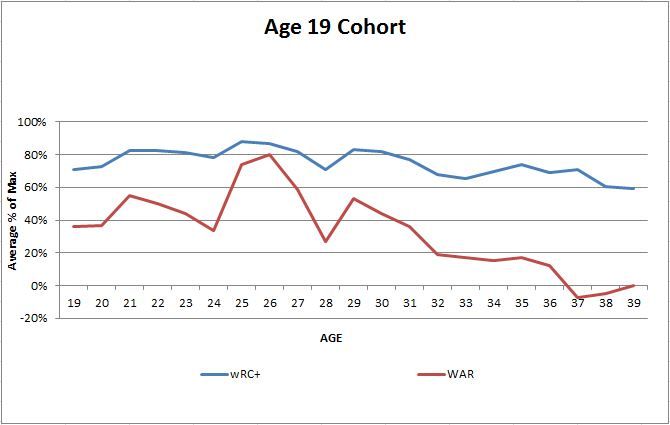
I’ve decided to break this final section in half and address the early development of run estimation statistics first, and then examine new ways to make these estimations next week. In Part 1, we examined the early development of batting statistics. In Part 2, we broke down the weaknesses of these statistics and introduced new averages based on “real and indisputable facts.” In Part 3, we will examine methods used to estimate the value of batting events in terms of their fundamental purpose: run creation.

The two main objectives of batters are to not cause an out and to advance as many bases as possible. These objectives exist as a way for batters to accomplish the most fundamental purpose of all players on offense: to create runs. The basic effective averages presented in Part 2 provide a simple way to observe the rate at which batters succeed at their main objectives, but they do not inform us on how those successes lead to the creation of runs. To gather this information, we’ll apply a method of estimating the run values of events that can trace its roots back nearly a century.

The earliest attempt to estimate the run value of batting events came in the March 1916 issue of Baseball Magazine. F.C. Lane, editor of the magazine, discussed the weakness of batting average as a measure of batting effectiveness in an article titled “Why the System of Batting Averages Should be Changed”:

“The system of keeping batting averages…gives the comparative number of times a player makes a hit without paying any attention to the importance of that hit. Home runs and scratch singles are all bulged together on the same footing, when everybody knows that one is vastly more important than the other.”

To address this issue, Lane considered the fundamental purpose of making hits.

“Hits are not made as mere spectacular displays of batting ability; they are made for a purpose, namely, to assist in the all-important labor of scoring runs. Their entire value lies in their value as run producers.”

In order to measure the “comparative ability” of batters, Lane suggests a general rule for evaluating hits:

“It would be grossly inaccurate to claim that a hit should be rated in value solely upon its direct and immediate effect in producing runs. The only rule to be applied is the average value of a hit in terms of runs produced under average conditions throughout a season.”

He then proposed a method to estimate the value of each type of hit based on the number of bases that the batter and all baserunners advanced on average during each type of hit. Lane’s premise was that each base was worth one-fourth of a run, as it takes the advancement through four bases for a player to secure a run. By accounting for all of the bases advanced by a batter and the baserunners due to a hit, he could determine the number of runs that the hit created. However, as the data necessary to actually implement this method did not exist in March 1916, the work done in this article was little more than a back-of-the-envelope calculation built on assumptions concerning how often baserunners were on base during hits and how far they tended to advance because of those hits.

As he wanted to conduct a rigorous analysis with this method, Lane spent the summer of 1916 compiling data on 1,000 hits from “a little over sixty-two games”[i] to aid him in this work. During these games, he would note “how far the man making the hit advanced, whether or not he scored, and also how far he advanced other runners, if any, who were occupying the bases at the time.” Additionally, in any instance when a batter who had made a hit was removed from the base paths due to a subsequent fielder’s choice, he would note how far the replacement baserunner advanced.

Lane presented this data in the January 1917 issue of Baseball Magazine in an article titled similarly to his earlier work: “Why the System of Batting Averages Should be Reformed.” Using the collected data, Lane developed two methods for estimating the run value that each type of hit provided for a team on average. The first method, the one he initially presented in March 1916, which I’ll call the “advancement” method,[ii] counted the total number of bases that the batter and the baserunners advanced during a hit, and any bases that were advanced to by batters on a fielder’s choice following a hit (an addition not included in the first article). For example, of the 1,000 hits Lane observed, 789 were singles. Those singles resulted in the batter advancing 789 bases, runners on base at the time of the singles advancing 603 bases, and batters on fielder’s choice plays following the singles advancing to 154 bases – a total of 1,546 bases. With each base estimated as being worth one-fourth of a run, these 1,546 bases yielded 386.5 runs – an average value of .490 runs per single. Lane repeated this process for doubles (.772 runs), triples (1.150 runs), and home runs (1.258 runs).

This was the method Lane first developed in his March 1916 article, but at some point during his research he decided that a second method, which I’ll call the “instrumentality” method, was more preferable.[iii] In this method, Lane considered the number of runs that were scored because of each hit (RBI), the runs scored by the batters that made each hit, and the runs scored by baserunners that reached on a fielder’s choice following a hit. For instance, of the 789 singles that Lane observed, there were 163 runs batted in, 182 runs scored by the batters that hit the singles, and 16 runs scored by runners that reached on a fielder’s choice following a single. The 361 runs “created” by the 789 singles yielded an average value of .457 runs per single. This method was repeated for doubles (.786 runs), triples (1.150), and home runs (1.551 runs).

In March 1917, Lane went one step further. In an article titled “The Base on Balls,” Lane decried the treatment of walks by the official statisticians and aimed to estimate their value. In 1887, the National League had counted walks as hits in an effort to reward batters for safely reaching base, but the sudden rise in batting averages was so off-putting that the method was quickly abandoned following the season. As Lane put it:

“…the same potent intellects who had been responsible for this wild orgy of batting reversed their august decision and declared that a base on balls was of no account, generally worthless and henceforth even forever should not redound to the credit of the batter who was responsible for such free transportation to first base.

The magnates of that far distant date evidently had never heard of such a thing as a happy medium…‘Whole hog or none’ was the noble slogan of the magnates of ’87. Having tried the ‘whole’ they decreed the ‘none’ and ‘none’ it has been ever since…

‘The easiest way’ might be adopted as a motto in baseball. It was simpler to say a base on balls was valueless than to find out what its value was.”

Lane attempted to correct this disservice by applying his instrumentality method to walks. Over the same sample of 63 games in which he collected information on the 1,000 hits, he observed 283 walks. Those walks yielded six runs batted in, 64 runs scored by the batter, and two runs scored by runners that replaced the initial batter due to a fielder’s choice. Through this method, Lane calculated the average value of a walk as .254 runs.[iv]

Each method Lane used was certainly affected by his limited sample of data. The proportions of each type of hit that he observed were similar to the annual rates in 1916, but the examination of only 1,000 hits made it easy for randomness to affect the calculation, particularly for the low-frequency events. Had five fewer runners been on first base at the time of the 29 home runs observed by Lane, the average value of a home run would have dropped from 1.258 runs to 1.129 runs using the advancement method and from 1.551 runs to 1.379 runs using the instrumentality method. It’s hard to trust values that are that so easily affected by a slight change in circumstances.

Lane was well aware of these limitations, but treated the work more as an exercise to prove the merit of his rationale, rather than an official calculation of the run values. In an article in the February 1917 issue of Baseball Magazine titled, “A Brand New System of Batting Averages,” he notes:

“Our sample home runs, which numbered but 29, were of course less accurate. But we did not even suggest that the values which were derived from the 1,000 hits should be incorporated as they stand in the batting averages. Our labors were undertaken merely to show what might be done by keeping a sufficiently comprehensive record of the various hits…our data on home runs, though less complete than we could wish, probably wouldn’t vary a great deal from the general averages.”

In the same article, Lane applied the values calculated with the instrumentality method to the batting statistics of players from the 1916 season, creating a statistic he called Batting Effectiveness, which measured the number of runs per at-bat that a player created through hits. The leaderboard he included is the first example of batters being ranked with a run average since runs per game in the 1870s.

Lane didn’t have a wide audience ready to appreciate a run estimation of this kind, and it gained little notoriety going forward. In his March 1916 article, Lane referenced an exchange he had with the Secretary of the National League, John Heydler, concerning how batting average treats all hits equally. Heydler responded:

“…the system of giving as much credit to singles as to home runs is inaccurate…But it has never seemed practicable to use any other system. How, for instance, are you going to give the comparative values of home runs and singles?”

Seven years later, by which point Heydler had become President of the National League, the method to address this issue was chosen. In 1923, the National League adopted the slugging average—total bases on hits per at-bat—as its second official average.

While Lane’s work on run estimation faded away, another method to estimate the run value of individual batting events was introduced nearly five decades later in the July/August 1963 issue of Operations Research. A Canadian military strategist, with a passion for baseball, named George R. Lindsey wrote an article for the journal titled, “An Investigation of Strategies in Baseball.” In this article, Lindsey proposed a novel approach to measure the value of any event in baseball, including batting events.

The construction of Lindsey’s method began by observing all or parts of 373 games from 1959 through 1960 by radio, television, or personal attendance, compiling 6,399 half-innings of play-by-play data. With this information, he calculated P(r|T,B), “the probability that, between the time that a batter comes to the plate with T men out and the bases in state B,[v] and the end of the half-inning, the team will score exactly r runs.” For example, P(0|0,0), that is, the probability of exactly zero runs being scored from the time a batter comes to the plate with zero outs and the bases empty through the end of the half-inning, was found to be 74.7 percent; P(1|0,0) was 13.6 percent, P(2|0,0) was 6.8 percent, etc.

Lindsey used these probabilities to calculate the average number of runs a team could expect to score following the start of a plate appearance in each of the 24 out/base states: E(T,B).[vi] The table that Lindsey produced including these expected run averages reflects the earliest example of what we now call a run expectancy matrix.

With this tool in hand, Lindsey began tackling assorted questions in his paper, culminating with a section on “A Measure of Batting Effectiveness.” He suggested an approach to assessing batting effectiveness based on three assumptions:

“(a) that the ultimate purpose of the batter is to cause runs to be scored

(b) that the measure of the batting effectiveness of an individual should not depend on the situations that faced him when he came to the plate (since they were not brought about by his own actions), and

(c) that the probability of the batter making different kinds of hits is independent of the situation on the bases.”

Lindsey focused his measurement of batting effectiveness on hits. To estimate the run values of each type of hit, Lindsey observed that “a hit which converts situation {T,B} into {T,B′} increases the expected number of runs by E(T,B′) – E(T,B).” For example, a single hit in out/base state {0,0} will yield out/base state {0,1}. If you consult the table that I linked above, you’ll note that this creates a change in run expectancy, as calculated by Lindsey, of .352 runs (.813 – .461). By repeating this process for each of the 24 out/base states, and weighting the values based on the relative frequency in which each out/base state occurred, the average value of a single was found to be 0.41 runs.[vii] This was repeated for doubles (0.82 runs), triples (1.06 runs), and home runs (1.42 runs). By applying these weights to a player’s seasonal statistics, Lindsey created a measurement of batting effectiveness in terms of “equivalent runs” per time at bat.

Like with Lane’s methods, the work done by Lindsey was not widely appreciated at first. However, 21 years after his article was published in Operations Research, his system was repurposed and presented in The Hidden Game of Baseball by John Thorn and Pete Palmer—the man who helped make on base average an official statistic just a few years earlier. Using play-by-play accounts of 34 World Series games from 1956 through 1960,[viii] and simulations of games based on data from 1901 through 1977, Palmer rebuilt the run expectancy matrix that Lindsey introduced two decades earlier.

In addition to measuring the average value of singles (.46 runs), doubles (.80 runs), triples (1.02 runs), and home runs (1.40 runs) as Lindsey had done, Palmer also measured the value of walks and times hit by the pitcher (0.33 runs), as well as at-bats that ended with a batting “failure,” i.e. outs and reaches on an error (-0.25 runs). While I’ve already addressed issues with counting times reached on an error as a failure in Part 2, the principle of acknowledging the value produced when the batter failed was an important step forward from Lindsey’s work, and Lane’s before him. When an out occurs in a batter’s plate appearance, the batting team’s expected run total for the remainder of the half-inning decreases. When the batter fails to reach base safely, he not only doesn’t produce runs for his team, he takes away potential run production that was expected to occur. In this way, we can say that the batter created negative value—a decrease in expected runs—for the batting team.

Palmer applied these weights to a player’s seasonal totals, as Lindsey had done, and formed a statistic called Batter Runs reflecting the number of runs above average that a player produced in a season. Palmer’s work came during a significant period for the advancement of baseball statistics. Bill James had gained a wide audience with his annual Baseball Abstract by the early-1980s and The Hidden Game of Baseball was published in the midst of this new appreciation for complex analysis of baseball systems. While Lindsey and Lane’s work had been cast aside, there was finally an audience ready to acknowledge the value of run estimation.

Perhaps the most important effect of this new era of baseball analysis was the massive collection of data that began to occur in the background. Beginning in the 1980s, play-by-play accounts were being constructed to cover entire seasons of games. Lane had tracked 1,000 hits, Lindsey had observed 6,399 half-innings, and Palmer had used just 34 games (along with computer simulations) to estimate the run values of batting events. By the 2000s, play-by-play accounts of tens of thousands of games were publically available online.

Gone were the days of estimations weakened by small sample sizes. With complete play-by-play data available for every game over a given time period, the construction of a run expectancy matrix was effectively no longer an estimation. Rather, it could now reflect, over that period of games, the average number of runs that scored between a given out/base state and the end of the half-inning, with near absolute accuracy.[ix] Similarly, assumptions about how baserunners moved around the bases during batting events were no longer necessary. Information concerning the specific effects on the out/base state caused by every event in every baseball game over many seasons could be found with relative ease.

In 2007, Tom M. Tango,[x] Mitchel G. Lichtman, and Andrew E. Dolphin took advantage of this gluttony of information and reconstructed Lindsey’s “linear weights” method (as named by Palmer) in The Book: Playing the Percentages in Baseball. Tango et al. used data from every game from 1999 through 2002 to build an updated run expectancy matrix. Using it, along with the play-by-play data from the same period, they calculated the average value of a variety of events, most notably eight batting events: singles (.475 runs), doubles (.776 runs), triples (1.070 runs), home runs (1.397 runs), non-intentional walks (.323 runs), times hit by the pitcher (.352 runs), times reached on an error (.508 runs). and outs (-.299 runs). These events were isolated to form an estimate of a player’s general batting effectiveness called weighted On Base Average (wOBA).

Across 90 years, here were five different attempts to estimate the number of runs that batters created, with varying amounts of data, using varying methods of analysis, in varying run scoring environments, and yet the estimations all end up looking quite similar.

Beyond the general goal of measuring the run value of certain batting events, each of these methods had another thing in common: each method was designed to measure the effectiveness of batters. Lane and Lindsey focused exclusively on hits,  the traditional measures of batting effectiveness.[xi] Palmer added in the “on base” statistics of walks and times hit by the pitcher, while also accounting for the value of those times the batter showed ineffectiveness. Tango et al. threw away intentional walks as irrelevant events when it came to testing a batter’s skill, while crediting the positive value created by batters when reaching on an error.

The same inconsistencies present in the traditional averages for deciding when to reward batters for succeeding and when to punish them for failing are present in these run estimators. In the same way we created the basic effective averages in Part 2, we should establish a baseline for the total production in terms of runs caused by a batter’s plate appearances, independent of whether that production occurred due to batting effectiveness. We can later judge how much of that value we believe was caused by outside forces, but we should begin with this foundation. This will be the goal of the final part of this paper.

[i] In his article the next month, Lane says explicitly that he observed 63 games, but I prefer his unnecessarily roundabout description in the January 1917 article.

[ii] I’ve named these methods because Lane didn’t, and it can get confusing to keep going back and forth between the two methods without using distinguishing names.

[iii] Lane never explains why exactly he prefers this method, and just states that it “may be safely employed as the more exact value of the two.” He continues, “the better method of determining the value of a hit is…in the number of runs which score through its instrumentality than through the number of bases piled-up for the team which made it.” This may be true, but he never proves it explicitly. Nevertheless, the “instrumentality” method was the only one he used going forward.

[iv] This value has often been misrepresented as .164 runs in past research due to a separate table from Lane’s article. That table reflected the value of each hit, and walks, with respect to the value of a home run. Walks were worth 16.4 percent of the value a home run (.254 / 1.551), but this is obviously not the same as the run value of a base on balls.

[v] The base states, B, are the various arrangements of runners on the bases: bases empty (0), man-on-first (1), man-on-second (2), man-on-third (3), men-on-first-and-second (12), men-on-first-and-third (13), men-on-second-and-third (23), and the bases loaded (123).

[vi] The calculation of these expected run averages involved an infinite summation of each possible number of runs that could score (0, 1, 2, 3,…) with respect to the probability that that number of runs would score. For instance,  here are some of the terms for E(0,0):

E(0,0) = (0 runs * P(0|0,0)) + (1 run * P(1|0,0)) + (2 runs * P(2|0,0)) + … + (∞ runs * P(∞|0,0))

E(0,0) = (0 runs * .747) + (1 run * .136) + (2 runs* .068) + … + (∞ runs * .000)

E(0,0) = .461 runs

Lindsey could have just as easily found E(T,B) by finding the total number of runs that scored following the beginning of all plate appearances in a given out/base state through the end of the inning, R(T,B), and dividing that by the number of plate appearances to occur in that out/base state, N(T,B), as follows:

E(T,B) = Total Runs (T,B) / Plate Appearances (T,B) = R(T,B) / N(T,B)

This is the method generally used today to construct run expectancy matrices, but Lindsey’s approach works just as well.

[vii] To simplify his estimations, Lindsey made certain assumptions about how baserunners tend to move during hits, similar to the assumptions Lane made in his initial March 1916 article. Specifically, he assumed that “runners always score from second or third base on any safe hit, score from first on a triple, go from first to third on 50 per cent of doubles, and score from first on the other 50 per cent of doubles.” While he did not track the movement of players in the same detail which Lane eventually employed, the total error caused by these assumptions did not have a significant effect on his results.

[viii] In The Hidden Game of Baseball, Thorn wrote that Palmer used data from “over 100 World Series contests,” but in the foreword to The Book: Playing the Percentages in Baseball, Palmer wrote that “the data I used which ended up in The Hidden Game of Baseball in the 1980s was obtained from the play-by-play accounts of thirty-five World Series games from 1956 to 1960 in the annual Sporting News Baseball Guides.” I’ll lean towards Palmer’s own words, though I’ve adjusted “thirty-five” down to 34 since there were only 34 World Series games over the period Palmer referenced.

[ix] The only limiting factor in the accuracy of a run expectancy matrix in the modern “big data” era is in the accuracy of those who record the play-by-play information and in the quality of the programs written to interpret the data. Additionally, the standard practice when building these matrices is to exclude all data from the home halves of the ninth inning or later, and any other partial innings. These innings do not follow the standard rules observed in every other half-inning, namely that they must end with three outs, and thus introduce bias into the data if included.

[x] The only nom de plume I’ve included in this history, as far as I’m aware.

[xi] Lane didn’t include walks in his Batting Effectiveness statistic, despite eventually calculating their value.

On May 20^th Peter O’Brien hit a massive home run to straight away center clearing the 32 foot tall batter’s eye at Arm & Hammer Park more the 400 feet from home plate.  O’Brien is currently 1 home run behind Joey Gallo, in what looks to be an exciting competition for the minor league home run title.  O’Brien isn’t as highly touted a prospect as Gallo, but he still has some of the most impressive power in the minor leagues.  Reggie Jackson saw O’Brien’s home run and said it was one of hardest hit balls in the minor leagues that he had ever seen (and Reggie knows a thing or two about tape measure home runs).

How hard was that ball actually hit?  It is impossible to figure out exactly how hard and how far the ball was hit from the available information.  You can however use basic physics to make a reasonable estimation.

Below I explain the assumptions and thought process I used to get to an estimate of how hard the ball was hit.  If that does not interest you, then just skip to the end to find out what it takes to impress Reggie Jackson. But, if you’re curios or skeptical stick around.

OBSERVATIONS

I started off by watching the video to see what information I could gather (O’Brien’s at bat starts at the 37 second mark in the video).

TIME OF FLIGHT From the crack of the bat, to the ball leaving the park – it appears to take 5 seconds. If you watched the video, you can tell this is not a perfect measurement since the camera doesn’t track the ball very closely. If you think you have a better estimation, let me know and I’ll rework the numbers.  

LOCATION LEAVING THE PARK  The ball was hit to straight away center. From the park dimensions we know when it left the park it was 407 feet from home plate and at least 32 feet in the air to clear the batter’s eye.

ASSUMPTIONS

COEFFICIENTS OF DRAG (Cd) – The Cd determines how much a ball will slow down as it moves through the air. I chose 0.35 for the Cd because it is right in the middle of the most frequently inferred Cd values for the home runs that Allan Nathan was looking at in this paper.In looking at the Cds of baseballs, Allan Nathan showed there is reason to believe that there is some significant (meaning greater than what can be explained by random measurement error) variation in Cd from one baseball to another.

ORIGIN OF BALL I assume the ball was 3.5 feet off the ground and 2 feet in front of home plate when it was hit.  These are the standard parameters in Dr. Nathan’s trajectory calculator. But what if the location is off by a foot? The effects of the origin on the trajectory are translational. One foot up, one foot higher. One foot down, one foot lower. The other observations and assumptions are more significant in determining the trajectory of the home run.

Using these assumptions and the trajectory calculator, I was able to determine the minimum speed and backspin a ball would need in order to clear the 32 foot batter’s eye 5 seconds after being hit at different launch angles.  The table below shows the vertical launch angle (in degrees), the back spin (in RMPs) and the speed of the balled ball (in MPH).

The graph shows a more visual representation of the trajectories in the table above (with the batter’s eye added in for reference).

http://i1025.photobucket.com/albums/y314/GWR87/OBrienhomerun_zpsb1507cf4.png

Looking at the graph you will notice that all of these balls would be scraping the top of the batter’s eye.  This makes sense because the table shows the minimum velocities and back spins needed for the ball to exactly clear the batter’s eye.

What is the slowest O’Brien could have hit the ball?

If you were in a rush, looking at the table you would think the slowest O’Brien could have hit the ball would be 101 MPH at 19^o. But, not so fast! The amount of backspin required for the ball to travel at that trajectory is humanly impossible.

What is a reasonable backspin?

I am highly skeptical of backspin values greater than 4,000 rpm based on the Baseball Prospectus article by Alan Nathan “How Far Did That Fly Ball Travel?.” The backspin on home runs Nathan examined ranged from 500 to 3,500 rpm, with most falling in around 2,000. The first 3 entries in the table have backspins of over 4,000 and can be eliminated as possibilities. If the ball with the 19^o launch angle only had 3,500 rpm of back spin it would have hit the batter’s eye less than 11 feet off the ground instead of clearing it.  Maybe you’re skeptical that I eliminated the 3^rd entry because it’s close to the 4,000 rpm cut off.  Think about it this way, if a player was able to hit a ball with over 4,000 rpm of back spin, they would have to be hitting at a much higher launch angle than 23^o (Higher launch angles generate greater spin while lower launch angles generate less spin).

The high launch angle trajectories with very little back spin (like the bottom three in the table) are also not very likely.  A ball hit with a 40^o launch angle would almost certainly have more than 4 rpm of back spin.  If the ball hit with the 40^o launch angle had 1,000 rmp of back spin (instead of 4) it would have been 70 feet off the ground, easily clearing the 32 foot batter’s eye.

Accounting for reasonable back spin, the slowest O’Brien could have hit the ball is 103.69 MPH at 25^o with 2,779rpm of backspin.

So what do all these observations and assumptions get us?

We can say that the ball was likely hit 103.69 MPH or harder, with a launch angle of 25^o or greater.  103.69 MPH launch velocity is not that impressive, it is essentially the league average launch velocity for a home run.  Distance wise, how impressive of a home runs was it? Unobstructed the ball would have landed at least 440 feet from home plate (assuming the 25^o scenario).  The ball probably went further than 440 because it did not scrape the batter’s eye. So, how rare is a 440+ foot home run? Last year during the regular season there were 160 home runs that went 440 feet or further, there were a total of 4661 home runs that season, meaning only 3.4% of all home runs were hit at least that far.

For those of you who wanted to just skip to the end. My educated guess is that the ball went at least 440 feet and left the bat at at least 103.69 MPH.

If you like this, you can read other articles on my blog GWRamblings, or follow me on twitter  @GWRambling

None of this would have been possible without Alan Nathan’s great work on the physics of baseball.  I used his trajectory calculator to do this, and I referenced his articles frequently to make sure I wasn’t way making stupid assumptions. The information on major league home run distance is based off of hittrackeronline.com

One of Dave Cameron’s articles a while back showed payroll allocations by age groups, and it shows that over the last five years or so more money is going to players in their prime years while less is being spent on players over 30.  That seems to be a logical thing for teams to do, but that trend can only continue for so long.  Eventually a point will be reached where older players are undervalued, and it might be possible that we are already there.

There are several things to keep in mind when comparing these age groups, and one of the biggest is the survivorship bias.  There is a natural attrition over time for players in general.  Let’s look at an example, and for all the following I will be using 2012 versus 2013 as a way to see what happens from year to year.  To look at survivorship, I looked at all position players in 2012 and then their contribution in 2013 to see how many disappeared the next year.  The players that were not in the 2013 year could be due to retirement, demotion, injury, etc.  I also took out a small group that played in both seasons, but were basically non-factors in 2013, for example Wilson Betemit played in both seasons, but in 2013 he only had 10 plate appearances.  The attrition rate for the age groups looks like this:

As you would expect, the attrition rate increases over time.  Players in their late teens and early 20s who make it to the majors are likely to be given opportunities in the near future, but as the age increases the probability of teams giving up on the player, major injury, or retirement goes up.  Players who make it from one group to the next have survived, and that is where the bias comes in.  By the time you get to the 36+ group a significant number of the players are really good because if they weren’t they would not have made it so far.  This ability to survive is also a reason why they should be getting a good chunk of the payroll.  As I will show you, it leads to steady play which teams should pay a premium for.

The next step is looking at performance risk among the groups.  To look at this I took each group’s performance in 2012 and compared it to the group’s performance in 2013, again only with survivors from year to year.  I looked at both wRC+ and WAR just to see if only the hitting component or overall performance behaved differently.

Further, to calculate a risk level I looked at the standard deviations of the differences (2013 minus 2012) for each player, but those are not directly comparable.  Standard deviation is higher for distributions with higher averages due to scaling issues.  For instance, the average 36+ player had a 95 wRC+ in 2012 versus, which is more than 10 wRC+ above the average 18 to 25 year old in the same year.  A 10% drop or increase  in production is therefore a larger absolute change for the 36+ player, so they naturally end up with a higher standard deviation.  To take care of this I calculated the standard deviation of the difference as a % of 2012 average production as the overall riskiness measure.

Don’t compare the wRC+ to WAR figures as there are again scaling issues, but look at the age groups.  A one standard deviation change is most volatile for the youngest age group, so the younger players are the most uncertain or most risky.  That is what we would expect as we have all seen prospects flame out.  The middle two groups are similarly volatile with the 31 to 35 group have a slightly lower risk level in the hitting for this sample and slightly higher overall play according to the WAR risk.  More years might need to be compared to see how consistent those groups are relatively.  The 36+ players are significantly less risky than the other ages.  If they decline by 1 standard deviation it will mean a smaller reduction in performance, less volatile and less risky.

The only thing that really hurts the older players is the aging curve.  They are more likely to see a decline in performance.  From the youngest group to oldest the percent of players who were worse in 2013 than they were in 2012 by wRC+ was 52.3%, 54.5%, 64.4%, 63.6%, and for WAR 52.9%, 48.7%, 56.7%, and 81.8%.  So it is more likely that the older players will see performance worse than the previous year, but again a drop for them will likely be smaller due to lower volatility and it is on average from a higher level of performance to begin with.

Older players are like buying bonds for your investment portfolio, you have a pretty good idea of what there going to pay in the next period with occasional defaults.  Younger players are more like growth stocks, you aren’t sure when or if they are going to pay dividends but when they do you can make huge returns.  Investors pay a premium for bonds (accept a lower rate of return) due to their stability, and teams pay more for older players than maybe their production seems to warrant for the same reason.

If you go back to the payroll allocation, part of the shift is in the number of players in each group.  The 31-35 year-olds no longer get the largest chunk of payroll in part because there are more 26 to 30 year-old players.  Baseball is getting younger overall, so a larger portion of the money going to younger players is inevitable.  The 18 to 25 group isn’t getting a large change in payroll allocation because they are generally under team control, but the teams are extending the players at that age with the money showing up as they get into the next couple age groups.  Like Chris Sale, who is making $3.5 million this year on the extension he signed (he’s 25), but when he is 26, 27, and 28 he will make 6, 9.15, and 12 million respectively.

So the 36+ group, as you can see only 4.7% of the players, used to make about 20% of the total salaries paid, but now they make 15 or 16% (I don’t have Dave’s exact numbers).  Is that premium fair, four times more of the allocation than they make up of the overall player pool?  That is a tough question, and one I am working on.  If anyone can give me tips on how to dump lots of player game logs, that is probably what I am going to do next, but haven’t figured out how to do it without eating up my entire life.  Being more certain on this sort of thing, and having a relative risk measure for players could make contracts a lot easier to understand and predict.