Using Decision Trees To Classify Yu Darvish Pitch Types
Last year, I wrote a post which outlined the application of a K Nearest Neighbors algorithm to make pitch classifications. This post will be, in some ways, an extension of that as pitches will yet again be classified using a machine learning model. However, as one might have presumed given this post’s title, the learner of choice here will be a decision tree. Additionally, this time around, instead of classifying pitches thrown over the course of a single game I will aim to classify pitches thrown by a single pitcher over the course of an entire season.
What follows will be divided into three sections: a brief conceptual explanation of decision tree learners, a description of the data and steps taken to train the decision tree model of choice here, and finally a run-through of the model’s results. I am not an expert on machine learning, but I believe that this is an interesting exercise that (very, very basically) highlights a powerful model using interesting baseball data. The work to support this post was conducted in scripting language R and with the direction of the book Machine Learning with R by Brett Lantz.
A Much-Too-Basic Explanation of Decision Trees
First and foremost, decision trees are classifiers. Given some quantity of information, decision trees classify/label observations. Decision trees might be used to classify beverages such as beer, wine, or spirits, or they might classify an image of skin as featuring cancerous cells or not. Here a decision tree will be used to classify a pitch type among several possibilities. Decision trees can classify binary variables (offering yes/no-type answers) or multiple variables (classifying pitches as either fastball, changeups, curveballs, sliders, etc.). Classifiers do not handle numeric predictions; various regression techniques/models are applied in those cases (although regression trees can draw upon both methods to some degree).
Second, decision trees can be applied as supervised learning models, meaning they are then applied to a labeled data set. Put another way, a supervised model has target values to predict. Using pitch classifications as an example, given the velocity and spin rate and vertical movement of a pitch, a supervised model makes a prediction based on those variables and then discovers how well it learned the task of pitch classification. The actual pitch classifications are, hence, labeled. Unsupervised learners do not have labeled data to check their work but rather run wild (unsupervised) searching for undiscovered patterns in data, among other things.
Decision trees are named what they are for a reason: when picturing these classifiers, it is potentially helpful to envision a tree where the question of interest sits at the base, or “root node.” From there and gradually up/outward, a series of yes/no questions are applied to observations: are these observed pitches thrown at greater or less than 85 mph? Do those sub-85 mph pitches have spin rates greater or less than 2200 rpm? Do those sub-85 mph & >2200 rpm pitches have more or less than 15 inches of vertical break? Each of those splits is called a “decision node,” and the increasing number of those nodes forms the cascading tree-like structure from which decision trees get their name. The endpoints of each of those series of nodes is referred to as a “leaf node” and includes a prediction, like “slider” or “wine.”
Decision trees are supported by an approach commonly referred to as “divide and conquer,” due to the fact that data are split again and again until the algorithm can offer a prediction, which it does when the remaining observations in a given subset are homogenous to an acceptable degree (although other stopping criterion can be set). Of note is that the first feature that the decision tree algorithm splits upon is ideally the most predictive feature/variable of the target class. Given this, in the example from the prior paragraph, it’s supposed that velocity is the most predictive variable for pitch classification.
Another way to picture this divide and conquer procedure is with a scatterplot in mind. Should we have, for instance, pitch velocity on one axis and pitch spin on the other and all data points with their accurate pitch-type labels, decision trees draw distinguishing lines between those points within the scatterplot where they deem most constructive to creating homogenous subsets. With this in mind, one key limitation of decision trees is that these splits are exclusively axis-parallel, meaning no diagonal splits are made within that scatterplot, only completely horizontal or vertical.
With any luck this has been a serviceable, albeit very limited, introduction to how decision trees work conceptually. Next is a description of our data and the process of training the model.
Cleaning Data & Training the Model
First, the data used for this quick project comes via Baseball Savant. I have selected pitch data over the course of the entire 2019 season from Yu Darvish. Darvish has long been one of my favorite pitchers, but more importantly for this exercise, he throws a broad array of pitches and threw a lot of pitches with the Cubs in 2019.
After pulling data for each pitch Darvish threw in 2019, there was a little wrangling/cleaning to be done. First, a couple pitch types were dropped: Darvish’s eephus and changeup. I did this because Baseball Savant only classified 14 (out of thousands of pitches) of Darvish’s 2019 pitches as one of those two pitch types. I also dropped data for pitches where no spin rate was recorded. To be clear, this was not a very academic move as, among other things, those pitches were not random: of 332 dropped pitches without spin rates, 298 were classified as cutters, 21 as sliders, and three as split-fingers. In a more formal context, those pitch types almost certainly would have remained as a part of the data set.
Finally, I trimmed the data to include only the features I wished to train the decision tree learner to predict pitch types:
- release_speed (velocity, in mph)
- release_pos_x (horizontal release position of the ball)
- release_pos_z (vertical release position of the ball)
- plate_x (horizontal position of the ball when crossing home plate)
- plate_z (vertical position of the ball when crossing home plate)
- pfx_x (horizontal movement of the ball)
- pfx_z (vertical movement of the ball)
- release_spin_rate (spin rate, in rpm)
- release_extension (extension in feet)
After applying these simple filters, the new data set included 2,512 pitches from Darvish in 2019. Following these preliminary steps, data was split into training and test data sets using a simple “hold out” method. By that method, a subset of observations, i.e. pitches (here 10%, or 251) were “held out” while the algorithm used the remaining 90% of data, or 2,261 observations, to train a model for predicting pitch types. The first (training) data set is used to train the model to predict pitches with labels available so that the model may glean its performance. The second (test) data set is then fed into the model to test the model’s performance predicting pitch types on data that it has not seen.
Next is the algorithm. There are plenty of types of decision trees. The iteration used here is the C5.0 algorithm which was developed, according to my reference book, by computer scientist J Ross Quinlan. It is said to “[have] become the industry standard for producing decision trees because it does well for most types of problems directly out of the box,” according to Brett Lantz.
Here is a grossly-abridged-and-in-no-way-complete summary of the C5.0 algorithm at work: The C5.0 algorithm splits data based on entropy, or diversity (high entropy equates to high diversity among labels in data subsets), and it finds splits that reduce entropy among subsets. On top of this task, the C5.0 algorithm must consider entropy among all the subsets that it splits and weigh their varying levels of entropy based on the number of observations in those subsets. The increased homogeneity that comes with making any particular split is called the “information gain,” and splits stop when there is no longer any information gain.
Testing the Model & Other Considerations
After cleaning the original data and splitting it into training and test data sets, R makes things pretty easy. With the support of various R packages written by folks in the R community and made widely available, training a C5.0 algorithm on the Darvish pitch data is as simple as a few lines of code.
After the training phase, the model is instructed to predict the classifications of the remaining 251 pitches. Below is a snippet of the output created by R for a visual summary of that process.

You might read the output above as a series of if/then statements. Should a pitch have less than or equal to 0.08 inches of horizontal movement (in one direction, mind you), a spin axis less than 213 degrees, release spin of less than 1758 rpm, and a velocity of less than 90.4 mph, it will be classified as a splitter. Reading the output in the top-down manner reinforces the cascading nature of the decision tree’s divide and conquer heuristic.
As mentioned in the first section, the first split is ideally the most predictive of the classification of interest. For the C5.0 algorithm, it looks like Darvish’s horizontal pitch movement is the most predictive feature for classifying his pitch types, followed by spin axis, spin rate, and release speed. Anecdotally, this makes a fair amount of sense, although it did come as a bit of a surprise to see horizontal movement at the top of the list (although upon just a little reflection this makes sense, as glove-side versus arm-side movement represents a pretty clear distinction among pitches).
This is all well and good, but how did the C5.0 algorithm perform?
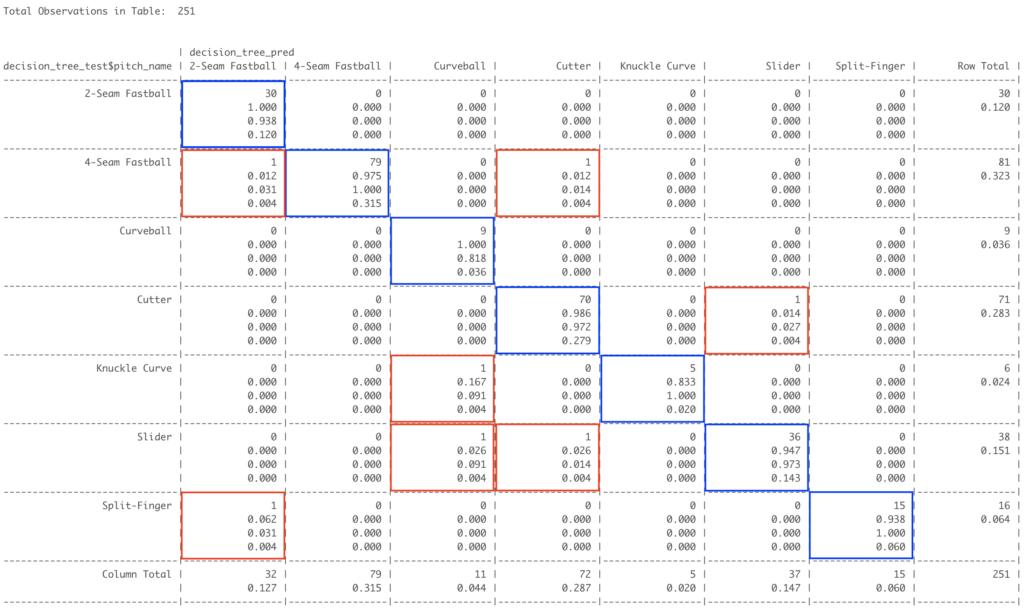
While there are a number of different measures of performance for any given type of prediction or algorithm, raw accuracy is an obvious measure of success. A good way to very simply and intuitively illustrate levels of accuracy is through a cross table, which juxtaposes predictions on one axis (here the horizontal axis) and actual classifications on the other (vertical). Below is the cross table for the C5.0 algorithm on Darvish pitch data (click to enlarge).
In a sentence, the fourth/cutter column of this cross table might be captured by saying that the C5.0 algorithm predicted 72 pitches to be classified as cutters, and 70 of those predictions were correct, while one four-seam fastball and one slider were misclassified as cutters. In all, seven of 251 pitches that the algorithm did not have labeled data for were classified correctly, or 97.2%. For those curious or who might have read the prior write-up on K-NN algorithm, I also applied that technique and the result was 92% accuracy.
There are any number of further adjustments available to tune these models or apply ensemble methods (like boosting, bagging, or random forests), none of which I will cover here. There are also additional ways of defining model success other than raw accuracy (Kappa statistics, choosing to weigh different types of mistakes to varying degrees, etc.). The point being that what is covered here really represents a snowflake on the tip of the iceberg. But still, I found it to be a fruitful exercise that gave way too strong of accuracy with pretty modest computational effort.
This post is adapted from my blog, which can be found here.

Awesome stuff, Ben. Simple yet insightful work like this is a great foundation.
One of the more useful parts of a decision tree is that they can use missing values as a part of the attribute. I.e., the absence of spin data for those pitches in question might have actually helped the model predict it was a cutter.
I’d also love to see the decision tree plotted out. It might get busy, but zooming in on specific pitches would be super cool to see. That can be done easily in R too.
Thanks! I appreciate that. Also, re: missing values, that’s not something I knew so thanks for the heads up. I imagine given that cutters appeared particularly predisposed to missing spin rates that would have been useful information for the C5.0 algorithm too. In any event, exciting things to keep learning about!
Heck I sure learned from reading this! Great job again