Projecting BABIP Using Batted Ball Data

Hi everybody, this is my first post here. Today, I’ll be sharing some of my BABIP research with you. There will probably be several more in the near future.

Now, I don’t know about you, but Voros McCracken’s famous thesis stating that pitchers have practically no control over their batting average on balls in play (BABIP) always seemed counterintuitive to me, ever since I heard it about 10 years ago. Basically, my thought this whole time was that if an Average Joe were pitching to an MLB lineup, the hitters would rarely be fooled by the pitches, and would be crushing most of them, making it very tough on the fielders. Think Home Run Derby (only with a lot more walks). Now, the worst MLB pitcher is a lot closer in ability to the best pitcher than he is to an Average Joe, but there still must be a spectrum amongst MLB pitchers relating to their BABIP, I figured. After crunching some numbers, I have to say that intuition hasn’t completely failed me.

This is going to be a long article, so if you want the main point right here, right now, it’s this: in the long run, about 40% or more of the difference in pitchers’ BABIPs can be explained by two factors that are independent of their team’s defense: how often batters hit infield fly balls and line drives off of them. It is more difficult to predict on a yearly basis, where I can only say that those factors can predict over 22% of the difference. Line drive rates are fairly inconsistent, but pop fly rates are among the more predictable pitching stats (about as much as K/BB). I’ll explain the formula at the very end of the article.

Now, for those of you who enjoy delving a lot deeper into topics than is necessary, or who love the word “correlation” (or generous use of parentheses), here you go:

For what I’m about to get into, my data set was composed only of pitchers with a qualifying number of innings pitched per season, from 1970-2012. I could have gone further back than that, but the further you go, the more you start dealing with issues like different stadiums, and even different gloves. I know that using only qualified pitchers arguably introduces bias (the really bad pitchers don’t get that many IP), but I feel it’s necessary to avoid fluky results.

A quick refresher on correlations: they range from -1 to +1, with +1 meaning when one factor increases, the other one does too in a perfectly predictable way; -1 indicates they move in perfectly opposite directions; and 0 meaning there is no apparent linear relationship between the two.  It depends on who you ask (and what the subject matter is), but if the correlation is over 0.5 (or under -0.5), it is generally considered “strong,” while if it’s less than 0.1 away from 0, it’s considered very weak or negligible.  A strong correlation indicates the two factors are connected, but not necessarily that one causes the other (they could both be caused by a third factor, for example).

The table below shows how well, on average, a pitcher’s BABIP in a given year correlates to past performances, in terms of the past year, the past two consecutive years, the past 3 consecutive, and the past 3 or more qualifying seasons out of the past 5 (using innings-weighted averages):

	Correlation	R-Squared
1-year	0.239	0.057
2-year	0.262	0.069
3-year	0.327	0.107
3+ of last 5	0.324	0.105

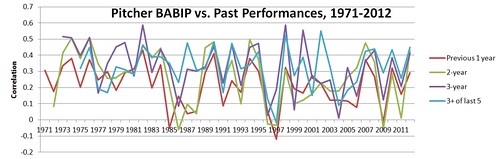
So, we see that overall, perhaps about 10% of the variation in pitchers’ BABIPs in any given year can be predicted by the past BABIPs of those pitchers. How much of that is due to the pitcher, as opposed to their defense, or even where they play, is up for debate. The chart shows how important the sample can be when you’re looking at BABIP, as the pattern is very inconsistent, but definitely real.  For a little context, a pitcher’s ERA’s correlated to his past ERAs only slightly better, in the long run:

1 year	0.322
2-year	0.347
3-year	0.376
3+ of last 5	0.362

Alright, I have 2 data sets I’ll be referring to over the rest of the article: 2007-2012 for anything PitchF/X related, but 2002-2012 as my main data set (assume I’m talking about this one unless otherwise noted). They both go back as far back as was possible to get the needed data. I know there are valid concerns about changes in the use of infield shifts altering BABIP rates in recent years, but with something with as much “noise” as BABIP, I think a lot of years’ worth of data is needed to see the underlying patterns.

In the upcoming correlation tables, green highlights indicate that higher values of the stat may lead to a lower BABIP (good news for the pitcher, obviously), whereas red indicates they may lead to a higher BABIP. Of course, correlation does not necessarily imply causation. Black stats are there for comparison, and to satisfy curiosities. These are based on the whole span of the data, not single seasons.

BABIP

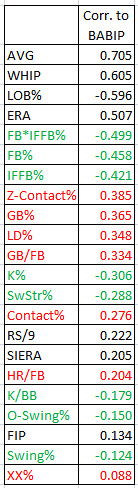
The combined stat FB%*IFFB% (sometimes denoted as FB*IFFB%, to save space) indicates the total percentage of balls in play that are infield popups.  I think the idea that this is perhaps one of the most significant inputs to BABIP should come as no surprise, as they’re pretty much automatic outs.

Z-Contact%, the percentage of swung-on balls thrown in the zone that are made contact with, turns out to be very important, but as I’ll show you, is largely made superfluous by its strong correlation to infield popups.

I think it makes perfect sense that groundballs and especially line drives both lead to higher BABIPs; they both make for harder putouts than the average fly ball.  You’ll see later that LD% is actually the more important of the two, not surprisingly.

More strikeouts being connected goes along with my Average Joe theory.  A pitcher fooling hitters will be reflected in terms of less frequent and weaker contact.

Run support (RS/9) is an interesting one; is the connection a reflection of better hitters also being worse fielders, or does it have to do with the park?

“XX” Pitches are unknown pitch types… perhaps they’re breaking pitches that don’t break like they’re supposed to, etc.  A weak connection overall, but it makes sense to consider them, I think.

Line Drive Percentage

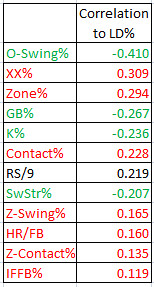
Getting hitters to swing at pitches outside the zone is a very good sign when it comes to allowing fewer line drives.  I’ll show you later how repeatable this, and other abilities, are.

The mystery (botched?) XX pitches loom large here.  A curveball that slips and doesn’t curve much is going to be close to as hittable as an Average Joe’s pitch.

Throwing in the zone more often puts you at risk for giving up more liners.  I think the trends suggest that you want to be a nibbler and to throw breaking pitches outside (probably mainly below or away) the zone, if you want to avoid giving up liners.  Not shocking, is it?

Thought I’d throw in run support again: defense has nothing to do with line drives, and the only park factors involved are maybe the batter’s   eye and the air (e.g. pitches breaking less in Colorado).  Perhaps this is really more about pitchers not being cautious when they have a big lead.

Infield Fly Balls

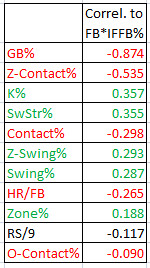
When it comes to infield popups, it’s no surprise that ground ball specialists don’t get many of them.

A popup pitcher gets hitters to swing and miss a lot at pitches in the zone (reflected by Z-Contact%).  He has dominant stuff.

Z-swing% shows that for a popup pitcher, the hitters are swinging more often at pitches in the zone.  Maybe that’s because they expect the pitcher to throw strikes, maybe the pitches look better to hit, or maybe the hitters are more prone to protect the plate due to an unfavorable count.

As with LD%, a higher HR/FB rate is an indication that hitters are making more solid contact with the pitches.

Contrary to LD%, pitching in the zone is beneficial for pitchers when it comes to popups.

Getting popups is less about nibbling, and more about attacking the zone and blowing it by hitters.  You’ll see later in the PitchF/X data how they tend to accomplish this.

How consistent are the rates of line drives and infield fly balls hit off of pitchers? Take a look:

Pitchers’ Line Drive Percentage (LD%) Correlation to Previous Years											Overall Average	2007-2012 Average
	2003	2004	2005	2006	2007	2008	2009	2010	2011	2012
Previous year	0.340	0.429	0.223	0.223	0.421	0.238	0.088	0.220	0.087	-0.009	0.226	0.174
Previous 2 years		0.476	0.203	0.243	0.554	0.284	0.180	0.185	-0.086	-0.030	0.223	0.181
Previous 3 years			0.502	0.289	0.471	0.491	0.295	0.230	0.012	-0.255	0.254	0.207
3+ of past 5					0.415	0.532	0.551	0.251	-0.079	0.041	0.285	0.285

So, line drive percentage, an important contributor to BABIP, is less predictable than BABIP itself. For a bit of context, though, the correlation in pitcher ERA to the previous year was 0.338, on average. It’s a very “noisy” statistic, and, I think it’s safe to say, is influenced somewhat by the pitcher, but not nearly as much as…

Pitchers’ Infield Fly Ball Percentage (FB%*IFFB%) Correlation to Previous Years											Overall Average	2007-2012 Average
	2003	2004	2005	2006	2007	2008	2009	2010	2011	2012
Previous year	0.616	0.720	0.675	0.609	0.705	0.633	0.581	0.518	0.686	0.524	0.627	0.608
Previous 2 years		0.748	0.749	0.639	0.735	0.705	0.516	0.595	0.634	0.664	0.665	0.642
Previous 3 years			0.768	0.714	0.732	0.691	0.599	0.728	0.655	0.568	0.682	0.662
3+ of past 5					0.701	0.685	0.618	0.768	0.656	0.598	0.671	0.671

Based on this, it would seem that close to half of the differences in popup rate between pitchers can be attributed directly to the pitchers’ attibutes. You may wonder why I would put so much emphasis on an occurrence such as infield popups, which happens on a little less than 4% of balls in play. Well, besides being automatic outs by themselves, I think it’s reasonable to assume that they are also a sign of less sharply-hit fly balls in general.

For the PitchF/X data I’m about to get into, I ignore velocity and movement for any type of pitch that was thrown less than 5% of the time by the pitcher. This was important to avoid skewing the correlations with fluky data, caused by PitchF/X measurement or pitch identification errors. A level as high as 5% was chosen because the pitch has to be a meaningful contributor to the pitcher’s arsenal to take its effects on his overall numbers seriously. A better analysis would also look at BIBIP results specific to each pitch type, but I’ll have to leave that to somebody else who has that data.

Here are the sample sizes for each pitch type (i.e., the number of pitchers who threw that pitch at least 5% of the time):

Pitch Type	Qualifying Pitchers
FA (4-seam fastball)	285
SL (Slider)	240
CH (Changeup)	234
CU (Curve)	188
FT (2-seam fastball)	123
SI (Sinker)	84
FC (Cutter)	78
FS (Splitter)	21

With these numbers in mind, take the results of the FS (splitter) movement and velocity correlations with a grain of salt. In the following lists, “X” indicates horizontal movement (e.g. FA-X for 4-seamers), “Z” indicates vertical, and “abs” indicates that I’m looking at the absolute value of the movement (i.e. movement to the left is as good as right, up as good as down). I omit the absolute value figure when its correlation is the same or worse than the non-absolute. By the way, I removed knuckleballs, eephuses, and knuckle-curves from these PitchF/X analyses due to their rarity.

Here’s the best explanation I’ve come across when it comes to PitchF/X movement . The summary is that a positive Z-value means the pitch has backspin that keeps it from dropping, whereas a negative Z indicates topspin (like a curveball) and therefore a drop; 0 means the ball has neither topspin nor backspin. For X values, negative means that from the catcher’s perpective, the ball breaks left, while positive means it breaks right. Absolute values are probably more significant for X (horizontal) movement for these reasons, as righties ought to have opposite movement from lefties in the horizontal axis, if I understand it correctly. Sidearm throwers do have odd vertical values, though (their fastballs have topspin, if anything).

BABIP   (Pitch F/X)

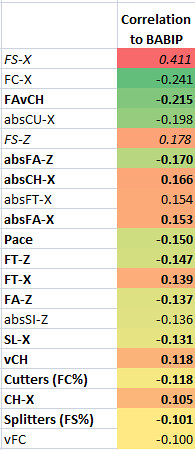
So, the PitchF/X data for BABIP overall doesn’t have   spectacular results. As we saw above, the methods for preventing line drives   vs. the methods for getting popups are a bit at odds, however, so that’s not surprising.

If we can take it seriously (and I don’t think we can, due to   sample size), FS-X (horizontal movement on the splitter) is apparently   undesirable for the pitcher, when in the positive direction (to the right of   the catcher). Meanwhile, a cutter that moves more to the right is apparently   helpful to the pitcher, if they can throw it.

FAvCH, a construction of mine (I’m probably not the first), is   the difference in velocities between the pitcher’s 4-seam fastball and his   changeup. Not surprisingly, a bigger gap correlates to a lower BABIP.   Pitchers who purposely change speeds on their fastballs probably see some of   this effect too, though I don’t have the data to prove that.

The   absolute vertical movement on the pitcher’s fastball is connected to a lower   BABIP.  It seems movement is a lot more   important than speed when it comes to fastballs and BABIP (vFA had basically no correlation).

Greater horizontal changeup movement in either direction was correlated to higher BABIPs.  However, vertical movement had   no correlation to BABIP.

Pace is an interesting one; it shows pitchers who wait longer in-between pitches tend towards lower BABIPs.  Who knows why?

Line Drive Percentage (Pitch F/X)

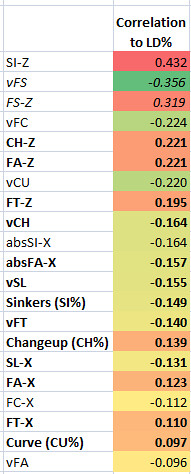
The profile of a line-drive preventer reads: 1) has good sinking pitches, and; 2) is a hard-thrower. It’s a hard thing to predict, though.

More drop on sinkers correlates fairly well with a lower line drive rate (SI-Z is also the strongest predictor of ground ball rates, with a -0.74 correlation).

Again, I wouldn’t take the splitter data (FS) too seriously due to how few pitchers rely on the pitch, but the data suggests a fast, sinking splitter is pretty useful here.

On the other hand, almost every pitcher throws a changeup, and they all throw 4-seamers, so it seems clear that more drop on the changeup (CH-Z) and 4-seam (FA-Z) are correlated with a higher LD%, though not as much as they are with ground ball percentage (GB%), (-0.421 and -0.685 respectively).

Faster pitches in general seem to lead to all be connected to a lower LD%. That seems logical – the hitters have less time to judge the location and movement of the pitch, and therefore won’t square it up as well. The connection is much weaker than it is to strikeout rates, as I’ll show you later, for comparison purposes.

As you see, there aren’t any particularly strong correlations in this data. Line drives are only semi-predictable (as I’ll demonstrate later), so that’s to be expected. Don’t worry, though – the pop fly data is more encouraging.

Infield Fly Balls (Pitch F/X)

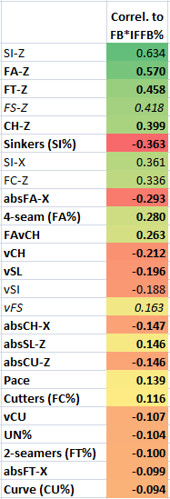
A fastball with more “rise” (technically, less drop) leads to more popups. I think that’s pretty much a slam dunk, based on this information (well, and logic).

A popup pitcher throws a lot of 4-seam fastballs, and not many sinkers and other sinking pitches. He also changes speeds well (i.e. as far as FAvCH, which has no correlation to LD%, by the way).

Fastball speed has no correlation to infield fly ball rate, but apparently you’re better off complementing your average-speed (but high-spin) fastball with some slow changeups, sliders, and sinkers, if you’re after popups – as long as they have plenty of backspin.

Pace shows up here. Take your time, I guess.

UN% are unknown pitches, like XX% earlier, only it’s probably harder to confuse PitchF/X. Once again, they are not a good sign for a pitcher, though.

Next, I’ll show you how these correlate with strikeout rates, because, hey, why not. Well, pitchers with high strikeout rates tend to have low BABIPs (-0.3 correlation), so it is relevant in that regard. Plus, I think it’s useful for context, to see how these numbers correlate to something that it’s pretty well accepted that pitchers have a good amount of control over (there’s a 0.787 year-to-year correlation for K%, by the way)

Strikeouts   (Pitch F/X)

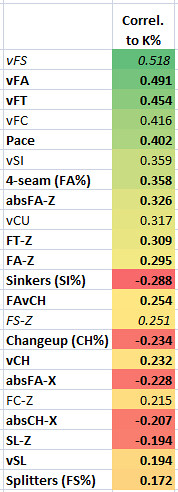
Velocity is king when it comes to strikeouts, it seems.  A higher percentage of 4-seamers is also fairly helpful.

Pace – wow, apparently making the batter wait is pretty useful   in getting strikeouts. But, you never know, with correlation – maybe   hard-throwers need more rest between pitches, so the pace is just a   side-effect. I’d have to do a regression to try to weed things out, but   that’s tricky when there are as many factors as these involved.

A “rising” fastball isn’t as important here as it is for   getting popups, but is still one of the main factors. This, along with other   shared factors, such as using more 4-seamers, fewer sinkers and greater   changes of speed, is probably why strikeout pitchers tend to get more popups.

So, hopefully by now I’ve brainwashed you through sheer repetition convinced you that pitchers do have some control over their BABIP, and that there are even particular traits that can explain how they influence it. Even though, altogether, only about 10% of the differences between BABIPs can be attributed to the pitchers themselves, this doesn’t mean that there aren’t certain pitchers who you can’t expect to have a low BABIP on a fairly consistent basis. Especially in the case of pitchers who get a lot of infield fly balls, I think you can.

So, without further ado, this is the formula of mine with the best mix of simplicity and accuracy when it comes to explaining a pitcher’s BABIP:

xBABIP = 0.4*LD% – 0.6*FB%*IFFB% + 0.235

In the long run, this formula correlates with a pitcher’s BABIP at 0.628, and is accurate to within 0.0096, on average. As a comparison, David Appelman’s 3-factor model from 2008, which was the best formula I am aware of that predates this one, has a 0.572 correlation to actual BABIP, and is accurate to within only 0.0148 (though if you subtract 0.01276 from the result of the formula, it’s accurate to within 0.0101, as his formula tends to overestimate BABIP). When comparing one individual season to the next, this formula has a 0.428 correlation to BABIP (vs. Appelman’s 0.351) and is only accurate to within 0.0157, however. Please let me know if you’re aware of any other formulas I should be testing it against.

The other factors I’ve tried to add in so far only make tiny improvements to the formula — HR/FB, for example, makes a very small improvement, but not enough to convince me that it’s really needed. Maybe next time, I’ll show up with a minor improvment, but I think it’s pretty clear that, at least in the long run, line drives and popups are the most important factors.

In the next installment, I plan to see if I can spot exceptional BABIP pitchers, and to explore how predictable BABIP is.

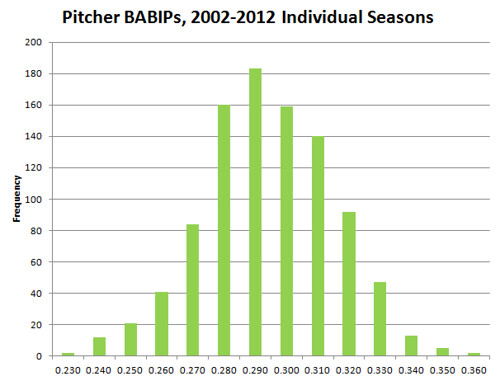
I leave you now with this gratuitous graph:

And a little extra context on how predictable stats are from year to year (average correlation between years for 2002-2012):

Mean YTY Correlation
GB/FB	0.864
GB%	0.838
FB%	0.823
SwStr%	0.804
Contact%	0.798
K%	0.787
OFFB%	0.787
Swing%	0.754
Z-Contact%	0.738
O-Contact%	0.702
BB%	0.689
K/BB	0.655
Z-Swing%	0.647
F-Strike%	0.636
FB*IFFB%	0.627
Zone%	0.598
O-Swing%	0.551
xBABIP	0.408
WHIP	0.408
IFFB%	0.361
ERA	0.338
HR/FB	0.262
XX%	0.260
Appelman’s	0.257
LD%	0.226
BABIP	0.184
LOB%	0.179
RS/9	0.153