BABIP and Innings Pitched (Plus, Explaining Popups)

In my last post on explaining pitchers’ BABIPs by way of their batted ball rates, I was very careful to say that it was applicable in the long run, as it’s hard to be accurate over a short number of innings pitched, due to all the “noise” in BABIP (Batting Average on Balls In Play).  I only used pitchers with a qualifying number of innings pitched (IP) in the calculations, for that reason.  After writing the post, I did some messing around with the data, to find out just how much of an effect IP had on the predictability of BABIP.

Hold on to your propeller beanies, fellow stat geeks: the correlation between xBABIP and BABIP went from 0.805 when the minimum IP was set to 1500, to 0.632 at a 200 IP minimum, down to 0.518 at 50 IP.  OK, maybe it’s not that surprising.  Still, I thought I’d better show you how confident you can be in my xBABIP formula’s accuracy when you take the pitcher’s innings pitched into account.

The formula, again: xBABIP = 0.4*LD% – 0.6*FB%*IFFB% + 0.235

And remember, that formula is primarily meant to be a backwards-looking estimator of “true,” defense-neutral BABIP.  My next article will (probably) discuss another formula I’ve come up with that’s more forward-looking.

Here’s the raw scatter plot of BABIP against IP over my main 2002-2012 sample (using the overall numbers for each pitcher):

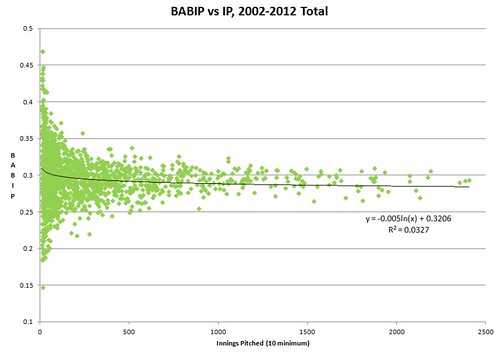
As you can see, towards the lower innings pitched, there is massive variation, but even with plenty of innings, there are still noteworthy differences between them that remain.   Also notice the outliers in the lower IP area tend towards high BABIPs — they probably didn’t get much time in the MLB due to their horrible BABIPs (whether that was due to bad luck or incompetence, who knows).

Next, we have a comparison of the Mean Absolute Error (MAE) between xBABIP and actual BABIP, according to innings pitched.  This was done by grouping pitchers into one of several IP categories, which you’ll see specified in the table below the graph.  You can interpret the MAE as the average amount that xBABIP will be off the mark from actual BABIP, either plus or minus.  It’s similar to RMSE (Root Mean Squared Error), except that RMSE basically gives an extra penalty for being further off the mark (which makes RMSE arguably more useful for comparing formulas, but more difficult to interpret and apply).

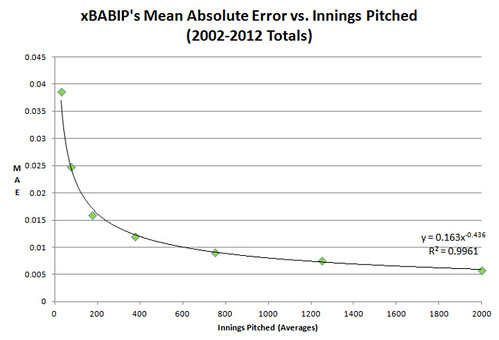
So, the formula xMAE = 0.163 * IP^-0.436 for xBABIP pretty much nails it with a 0.9961 r-squared (an r^2 of 1 is a perfect fit).  That’s the overall trend, anyway — it’s a lot noisier when applied to individual pitchers instead of averages, of course.  But I guess you could say the unpredictability is very predictable.  Here are the average MAEs for each range of IPs, and their expected MAEs according to the formula:

IP range	MAE	xMAE	Standard Deviation of BABIP	# of Pitchers
1500 to 2500	0.00591	0.00593	0.01204	37
1000 to 1500	0.00764	0.00728	0.01073	70
500 to 1000	0.00918	0.00909	0.01541	182
250 to 500	0.01201	0.01230	0.01841	279
100 to 250	0.01595	0.01715	0.02357	365
50 to 100	0.02483	0.02481	0.03419	267
10 to 50	0.03869	0.03700	0.05219	459

And here are some confidence measures:

IP range	Percent of the time MAE is less than:
	0.005	0.01	0.015	0.02	0.025	0.03	0.035	0.04
1500 to 2500	55.3%	76.3%	97.4%	100.0%	100.0%	100.0%	100.0%	100.0%
1000 to 1500	40.0%	70.0%	87.1%	95.7%	100.0%	100.0%	100.0%	100.0%
500 to 1000	29.7%	59.9%	84.6%	95.6%	96.2%	98.4%	99.5%	100.0%
250 to 500	26.2%	48.4%	65.2%	81.4%	91.0%	95.7%	98.6%	99.6%
100 to 250	21.1%	39.7%	58.4%	68.8%	80.0%	85.5%	91.0%	94.2%
50 to 100	12.7%	24.3%	36.7%	49.1%	57.3%	66.3%	71.5%	79.4%
10 to 50	6.5%	14.2%	19.4%	24.6%	29.1%	34.6%	40.5%	47.1%

So, you could say the standard 95% confidence interval can be achieved to within 0.020 points BABIP when there are over 500 IP.  However, when there are fewer than 100 IP of data to work with, there’s not much you can be very sure of.

 

Explaining Popups

If you read my last article, you know that I see popups (defined as FB%*IFFB%) as the main key to distinguishing pitchers’ BABIPs.  I took a little time to see if some of the factors I uncovered as being correlated to infield fly balls could be used to come up with an estimation of the rate.  Specifically, I went for factors that are no-doubt-about-it controlled by the pitcher.  Here are the variables:

xPU% = expected popup percentage (also known as xFB%*IFFB%)

FA% = percentage of 4-seam fastballs thrown

FAZ = vertical movement on 4-seamers (positive values means it rises relative to a spinless ball)

SI% = percentage of sinkers thrown

FAvCH = the difference in speed between the pitcher’s 4-seamer and changeup (=vFA – vCH)

Zone% = Percentage of pitches thrown in the zone

I won’t worry about trying to simplify the formula down, because I figure hardly anybody is actually going to try to use this:

xPU% = 0.00289*FA%*FAZ + 0.00189*FAZ – 0.01815*FA%  -0.00589*SI% + 0.00111*FAvCH + 0.05398*Zone% – 0.02040

The results: a 0.627 correlation to FB%*IFFB%, and a MAE of 0.789% (the mean and standard deviation of actual FB%*IFFB% are 3.616% and 1.308%, respectively).  Considering this doesn’t even take into account pitch locations (other than the vague Zone%), and that 5 variables are a pretty small piece of the overall puzzle, this seems pretty good to me.

If you’re curious, xPU% according to this formula has a -0.172 correlation to BABIP, -0.199 to HR/FB, and 0.388 to K% (which means pitchers with high xPU% tend to look better in all these areas), but on the downside, a 0.219 correlation to LD%.  It has almost no apparent connection to ERA (-0.045 correlation).

Updates to My Previous Article

I had included the stat Pace (which is the time a pitcher takes between pitches) as an interesting correlate to some factors (especially K%), but as J. Cross of Steamer Projections pointed out to me in a conversation on the Inside the Book site, Pace is mainly explained by % of innings as a starter.  For whatever reason, relievers tend to wait longer between pitches, but they also tend to strike out more hitters and generally have lower BABIPs as well.  I suspect the latter two points have a lot to do with my sample — the worse (or unluckier) relievers weren’t used enough to meet the IP requirements, so were excluded from consideration.

Matthew Cornwell, in that same discussion, brought up how extreme groundball pitchers tend to have lower than expected BABIPs.  I made a scatter plot and found that there appears to be some truth to that:

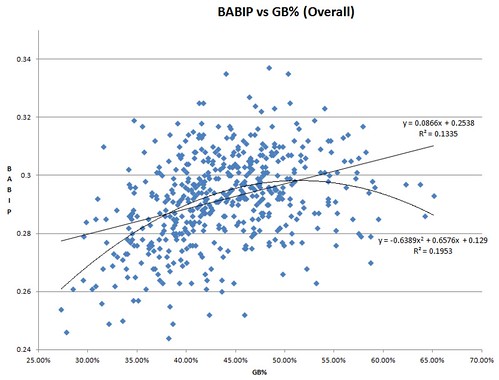
The quadratic equation that dips a bit towards the extreme GB% legitimately does work better than the linear one, as the r^2 numbers show.  Apparently, the new version of SIERA employs something along those lines as part of its formula.  It does make some sense — the extreme GB% pitchers are probably getting more of the ground ball equivalent of a popup: the chopper.  A chopper is far from an automatic out when the runner is fast, but it’s still a desirable thing overall, I’m sure.

A similar trend exists for OFFB%, or outfield fly ball percentage, which is FB% – FB%*IFFB%.  Actually, it’s an even stronger effect, although apparently IFFB%*FB% itself captures a lot of it.

I applied all this new knowledge to coming up with a new xBABIP formula, and the effects were pretty modest, I have to say.  Here it is:

xBABIP = 0.59*LD% – 0.31*FB%*IFFB% + 0.39*LD% – 0.22*LD%^2 + 0.21*OFFB% – 0.08*OFFB%^2

Over the same sample I used in the last article (qualified IP = 300+), there was only a 0.005 improvement in correlation, and a 0.00014 improvement in MAE, compared to the simple version.  Not a big upgrade for all that extra complexity, but there you have it.

Thanks again to J. Cross for providing me with the pitcher handedness data.  Unfortunately, there’s not a lot I can say about it, other than that lefties had a BABIP a little under 0.002 higher than righties over my data set.

…

It’s now almost a couple weeks after I initially submitted this article (I’m waiting for it to be published), and Eno Sarris just posted an article today that compares my formula (the simple version) to SIERA’s BABIP component, which uses the formula:  0.295 + 0.045*GB% – 0.103*K%.  I thought I’d put them head-to-head according to different criteria.  A couple I’ll introduce now: wMAE and wRMSE, which are the weighted versions of MAE and RMSE (in this case, weighted by innings pitched).  I’m also including results for J Cross’ formula, which is: 0.67*LD% + 0.24*GB% + 0.17*OFFB%  (OFFB% means outfield fly ball percentage, which is the fly balls that aren’t infield fly balls, of course).  This comparison, as usual, is for qualified pitchers (>300 IP) over the span of 2002-2012:

	xBABIP (simple)	xBABIP (complex)	SIERA BABIP	J Cross
Correlation to BABIP	0.62800	0.63434	0.40811	0.60725
MAE	0.00961	0.00947	0.01125	0.00980
wMAE	0.00854	0.00848	0.01041	0.00885
RMSE	0.01207	0.01201	0.01416	0.01244
wRMSE	0.01078	0.01076	0.01306	0.01127

As Eno correctly points out, putting a lot of weight on line drives does hurt the value for forecasting future BABIPs, since line drives are hard to predict.  But an article with a new formula tailored to predicting future BABIPs is in the works.  I’ll compare that formula to all of these.

I also have to say, as you can see from the effect of IP, don’t use only one season worth of batted ball data if you’re trying to project the next season — you’re much better off using several years’ worth.

…

I’ll leave you now with a couple of lists — the pitchers whose BABIPs from 2002-2012 are worst explained by the new, improved(?) formula, either due to good luck or misfortune, their defenses, or something else the formula just can’t explain.  They were selected for having the highest combinations of innings pitched and deviations from actual BABIP (but then listed according to the deviation afterwards):

“Luckiest” Pitchers

	IP	BABIP	xBABIP (simple)	xBABIP (complex)	Expected – Actual
Jeremy Hellickson	402.1	0.244	0.2817	0.2831	0.0391
Jason Isringhausen	508.1	0.252	0.2844	0.2875	0.0355
Billy Wagner	559.2	0.252	0.2833	0.2851	0.0331
Justin Duchscherer	440	0.261	0.2927	0.2935	0.0325
Kirk Rueter	648.1	0.285	0.3048	0.3066	0.0216
Greg Maddux	1457.1	0.287	0.3063	0.3080	0.0210
Tom Glavine	1293.1	0.284	0.3027	0.3049	0.0209
Roger Clemens	1029.2	0.28	0.2965	0.2989	0.0189
Russ Ortiz	951	0.287	0.3005	0.3034	0.0164
Tim Hudson	2108.2	0.279	0.2961	0.2952	0.0162
Chris Carpenter	1422	0.285	0.2992	0.3009	0.0159
Jon Garland	1896.2	0.283	0.2958	0.2984	0.0154
Carlos Zambrano	1951.1	0.277	0.2886	0.2918	0.0148
Cory Lidle	951.1	0.295	0.3070	0.3096	0.0146
Matt Cain	1536.2	0.264	0.2779	0.2784	0.0144
Barry Zito	2129.1	0.269	0.2816	0.2830	0.0140
Kenny Rogers	1253.1	0.294	0.3048	0.3073	0.0133
Ted Lilly	1807.1	0.265	0.2765	0.2761	0.0111
Johan Santana	1896	0.272	0.2803	0.2814	0.0094
Roy Halladay	2351	0.29	0.2942	0.2961	0.0061

“Unluckiest” Pitchers

	IP	BABIP	xBABIP (simple)	xBABIP (complex)	Expected – Actual
Felipe Paulino	385.1	0.335	0.2917	0.2916	-0.0434
Manny Parra	513	0.337	0.3012	0.3031	-0.0339
Kevin Slowey	532.2	0.31	0.2845	0.2802	-0.0298
Shawn Camp	566	0.323	0.2957	0.2963	-0.0267
Kyle Davies	768	0.318	0.2933	0.2932	-0.0248
Scott Kazmir	1022	0.302	0.2788	0.2790	-0.0230
Sidney Ponson	1055	0.318	0.2977	0.2994	-0.0186
Jeff Francis	1178.2	0.313	0.2923	0.2945	-0.0185
Scott Baker	958	0.302	0.2851	0.2838	-0.0182
Max Scherzer	804.2	0.312	0.2930	0.2939	-0.0181
Kelvim Escobar	916.1	0.304	0.2852	0.2873	-0.0167
Zach Duke	1054.2	0.323	0.3047	0.3063	-0.0167
Curt Schilling	1102.1	0.307	0.2902	0.2917	-0.0153
Chris Capuano	1162	0.297	0.2815	0.2839	-0.0131
Aaron Harang	1802	0.305	0.2918	0.2924	-0.0126
Zack Greinke	1492	0.308	0.2965	0.2977	-0.0103
Cliff Lee	1852.2	0.296	0.2859	0.2873	-0.0087
John Lackey	1876	0.309	0.2994	0.3010	-0.0080

 

 Lowest xBABIPs according to complex formula (new addition)

	BABIP	Simple	Complex	SIERA’s
Tyler Clippard	0.246	0.2438	0.2368	0.2743
Chris Young	0.254	0.2592	0.2530	0.2815
Russ Springer	0.261	0.2662	0.2603	0.2807
Carlos Marmol	0.257	0.2645	0.2625	0.2746
Takashi Saito	0.276	0.2606	0.2630	0.2779
Armando Benitez	0.25	0.2646	0.2634	0.2804
Octavio Dotel	0.269	0.2685	0.2657	0.2745
Robinson Tejeda	0.278	0.2674	0.2659	0.2856
Jon Rauch	0.273	0.2666	0.2661	0.2857
Scott Proctor	0.277	0.2711	0.2666	0.2848
Tim Wakefield	0.269	0.2642	0.2667	0.2919
Julio Mateo	0.261	0.2713	0.2678	0.2870
Luis Vizcaino	0.268	0.2659	0.2680	0.2847
David Hernandez	0.279	0.2724	0.2688	0.2798
Ramon Ramirez	0.272	0.2666	0.2690	0.2880
Joe Nathan	0.255	0.2680	0.2699	0.2763
Chad Cordero	0.257	0.2730	0.2701	0.2837
Orlando Hernandez	0.274	0.2687	0.2702	0.2855
Jered Weaver	0.271	0.2723	0.2702	0.2837