Introducing BERA: Another ERA Estimator to Confuse You All

Coming up with BERA… like its [almost] namesake might say, it was 90% mental, and the other half was physical.  OK, maybe he’d say something more along the lines of “what the hell is this…” but that’s beside the point.    By BERA, I mean BABIP-estimating ERA (or something like that… maybe one of you can come up with something fancier).  It’s an ERA estimator that’s along the lines of SIERA, only it’s simpler, and—dare I say—better.

You know, I started out not knowing where I was going, so I was worried I might not get there.  As you may recall, I’ve been pondering pitcher BABIPs for a little while here (see article 1 and article 2), and whereas my focus thus far had been on explaining big-picture, long-term BABIP stuff in terms of batted ball data, one question that remained was how well this info could be used to predict future BABIPs.  After monkeying around with answering that question, though, I saw that SIERA’s BABIP component could be improved upon, so I set to work in coming up with BERA.  In doing so, I definitely piggybacked off of FIP and a little of what SIERA had already done.  You can observe a lot just by watching, you know.   I’m also a believer in “less is more” (except for when it comes to the size of my articles, obviously), so I tried to go for the best compromise of simplicity and accuracy that I could.

I know I keep promising you something that will predict BABIPs better, but I figure this will be a bit more interesting to you all, so you’ll have to wait on that.

So, what’s the point of an ERA estimator?

To me, the answer is that it will give you the best guess of a pitcher’s “true” ERA, mainly free of the effects of their defenses and, ideally, of fluky performances.  Park adjustments are a nice thing too, but in the interest of keeping things simple, I’ve ignored that (you can apply after-the-fact park effects, if you want).

How do you measure how good an ERA estimator is? 

Well, I guess by comparing your estimated ERA to actual ERAs in surrounding years, in terms of correlation, mean absolute error (MAE), and/or root mean squared error (RMSE).  Why not just compare it to the current year’s ERA?  Because that would be too easy, that’s why… oh, but also, if you’re using unreliable numbers to come up with it, it’s not really that useful.  By unreliable, I mean that you can’t count on the numbers to stay very consistent from year to year.  The unreliability thing is why ERA estimators don’t include hits and LOB% as components, despite their major contributions to ERA in their same year, and also why some estimators minimize (e.g. xFIP) or ignore (e.g. SIERA) home runs.

If you want to minimize the impact of fluky seasons, using just one year’s worth of data isn’t a great idea; furthermore, setting the minimum innings pitched (IP) at only 40 compounds the problem.  However, that was the challenge I saw before me, so I went after it.  As you see from that link, Matt Swartz  has put the target on his SIERA’s back, by showing that it is actually better at predicting a pitcher’s ERA in the next year than actual full-blown ERA projection systems like PECOTA (by Nate Silver and company at Baseball Prospectus) and ZiPS (Dan Szymborski), which are in turn better than simple(r) ERA estimators like xFIP (Dave Studeman) and FIP (Tom Tango; independently, Clay Dreslough developed DICE, which is very similar).

However, SIERA is not without its detractors, such as Colin Wyers, who gave tearing SIERA a new one his best shot as a parting gift (the old version of SIERA had been offered by BP until the new version came here).  Not all of Colin’s criticisms stick, in my opinion, and some of them are less applicable to the new SIERA, but I have found it to be true that SIERA looks much less impressive as the sample size of innings for a pitcher increases.  It’s apparently very finely tuned to handle a 40 Innings Pitched (IP) minimum, but as I’m sure you know, the lower the minimum IP, the more “noise” you’ll see.  I think it may be the case that BABIP is picking up a lot of the noise and trying to make meaning of it; this is why, in my estimation, SIERA is soundly beaten by something as simple as FIP when you look at career numbers.  Of course, SIERA also gives itself the disadvantage of not considering home runs.

Yes, FIP picks up on long-term trends much better than SIERA — an 0.818 correlation to ERA vs. 0.722.  That’s for the whole of 2002-2012, 100 IP minimum, by the way.  But if the goal were simply to come up with something that matched ERA well, you’d want to go with something like:  2.6*WHIP + 42*HR/TBF – 9.5*LOB% + 6.423, which has a 0.979 correlation to ERA, and is correct to within an average of 0.127, vs. 0.371 for FIP.  Why not use that?  Well, all three of those factors are pretty unreliable from year-to-year, as you can see at the very bottom of my first article, with LOB% being especially so (well, HR/TBF is a bit better than the HR/FB you’ll see on that list, as the FB% connection is a lot more predictable than HR/FB, as it’s more influenced by the pitcher).  If you’re trying to predict one year’s ERA from the previous one’s numbers, those numbers aren’t going to work so well.

So, here’s my goal: a formula that can beat SIERA in estimating the next season’s ERA, while still holding its own against FIP in the long-term.  I’ll also include two other formulas that were tailored to each of those goals independently.  Why do I think that should be the goal?  Well, it will give more emphasis to the most repeatable stats, as does SIERA, without losing sight of the big picture, as SIERA arguably does somewhat.  If you don’t agree with that analysis, at least you’ll have 2 other formulas to either extreme to choose from.

Heeere’s BERA

Without further ado, the formula:

BERA = (32.6*HR + 11.4*BB – 7.9*K)/TBF + (5*LD + OFFB – 3.4*IFFB)/(FB+LD+GB) + 2.2*ZC% + 0.22*SIP% + 0.51

Where:

• SIP% is the percentage of a pitcher’s innings that were pitched as a starter.  You can find this (and all of these, really) most easily by setting up a custom leaderboard on FanGraphs (for this, divide “Start-IP” by total IP… ideally after converting 0.1 IP to 1/3, etc.).
• OFFB is Outfield Fly Balls, which is FB – IFFB
• FB+LD+GB represents the total of balls in play (including home runs)
• TBF, Total Batters Faced, is a.k.a. PA, Plate Appearances
• ZC% is Z-Contact%, which comes from the batted ball stats on FanGraphs (specifically, I used the non-PitchF/X version, as there were more years available), and represents the contact rate on pitches swung on that were in the zone.  You may recall that I pointed this out in my first article as one of the strongest correlates of infield popups and therefore BABIP.

A simplified version of the formula is:

11.4*BB% – 7.9*K% + 5*LD% + FB%*(1 – 4.4*IFFB%) + 32.6*(HR/TBF) + 2.2*ZC% + 0.22*SIP% + 0.51

This takes advantage of the fact that FanGraphs has already made these numbers into rates for you (except for HR/TBF and StartIP%, of course).  Be aware that on FanGraphs, there’s a big difference in how you have to interpret IFFB and IFFB% — IFFB is straightforward and represents the actual number of infield fly balls, whereas IFFB%, oddly, represents the percentage of fly balls that are infield flies… so, IFFB% really needs the context of fly ball percentage to be understood.  This is why in my previous articles I always used IFFB%*FB%.

As I said, I have a couple more formulas to show you — one tailored to guessing the ERAs of surrounding years based on one year’s worth of data (I’ll call it SBERA, for SIERA-Beating ERA) and another to defeat FIP in the long-term (FBERA):

SBERA = (8.8*HR + 5.4*BB – 6.2*K)/TBF + (1.7*LD + 5.1*OFFB – 0.6*GB)/(FB+LD+GB) – 7*[OFFB/(FB+LD+GB)]^2 + 2.4*ZC% + 0.36*SIP% + 1.26

FBERA = (57*HR + 15.1*BB – 7.9*K)/TBF + (6.7*LD – 10*IFFB)/(FB+LD+GB) + 0.2*SIP% + 1.793

You can see that the SIERA beater, being closer to SIERA itself, puts a lot more emphasis on SIP% and a lot less on HRs, whereas the FIP beater is kind of a combo between FIP and my original xBABIP formula (plus SIP%).   Warning: I’m not a big fan of SBERA — since it’s basically an attempt to out-SIERA SIERA, the potential flaws of SIERA are magnified within it.

Here’s the competition, via FanGraphs (with some paraphrasing…):

FIP = (13*HR + 3*BB – 2*SO)/IP + Annual “Fudge Factor” constant

xFIP = ((13*(FB% * League-average HR/FB rate))+(3*(BB+HBP))-(2*K))/IP + “Fudge Factor”

This “Fudge Factor” is also known as cFIP, and it’s there to tweak the league average FIP to be equal to the league average ERA in each year.  You can find it here: http://www.fangraphs.com/guts.aspx?type=cn .  SIERA also uses a similar annual factor, whereas mine don’t.  SIERA, though, doesn’t bring the average completely to the league mean — I didn’t crunch the numbers, but it looks to me it instead sets it to the mean ERA for pitchers with at least 40 IP.  As you can see, cFIP over my usual 2002-2012 sample has varied between 2.962 and 3.240.  Keep in mind that my formula doesn’t possess this unfair advantage when you see the comparisons.  Why don’t I use it?  Well, what it’s basically doing is scooting itself over closer to the correct answer, after it notices that it gave an incorrect answer.  So if the league ERA is about 0.1 higher than an unaltered FIP (from the previous year, e.g. 2006 vs. 2007) would predict, is that really a sign that all pitchers that year faced a tougher pitching environment, and thus we should add 0.1 to all their FIPs?  I really doubt it.  I find that difficult to justify, unless there’s some fundamental shift in the numbers involved between years; I think underlying reasons exist for the yearly ERA differences, and they should be explainable by other numbers, or else just be called “random chance” or “stochastic processes.”  I understand the point of this for practical purposes, especially when you’re using only 3 factors, such as in FIP, but I’m not sure how theoretically sound it is.  Now, a constant is one thing… but a constant that changes every year, after the fact… well, that’s a bit of an oxymoron, isn’t it?

Anyway, I’ll also include in the comparisons the results of predicting one year’s ERA using the previous year’s ERA.

There’s a newcomer I came across while writing this: pFIP, or Predictive FIP, by Glenn DuPaul at THT.  Glenn’s latest and greatest formula, as far as I’m aware, is pFIP = (17.5*HR + 7*BB – 9*K)/PA + Constant (typically ~5.18).

Oh, right, one more: SIERA.

The Comparisons

SIERA may be the reigning champion of the 40 IP weight class, but can it go toe-to-toe with the heavyweights?  Let’s look at the tale of the tape in this battle royale (with cheese).  These are looking at the total numbers (i.e., each pitcher’s average season) for all pitchers with at least 100 IP between 2002-2012 (the sample size: n=934 pitchers), and comparing the results of each formula against the pitcher’s actual ERA.  I’m using correlations, Mean Absolute Errors, and Root Mean Squared Errors here (I talk about these in my second article), along with the innings-pitched-weighted versions of each (which I think are more relevant, as they give more importance to the more reliable data).  Keep in mind that SIERA, xFIP, and FIP are helped considerably by their fudge factors when it comes to MAEs and RMSEs (but the fudge factors don’t affect the correlations), and that pFIP is intended to have fudge factors, but I’m just using the non-tweaked version, which is what Glenn showed us.  For some context, the cFIPs from 2002-2012 are, on average, 0.0608 away from their mean.  A reminder: for correlations, the closer to 1, the better; for everything else, the closer to 0, the better.

	SIERA	xFIP	FIP	pFIP	BERA	FBERA	SBERA
Correl.	0.7221	0.6904	0.8178	0.7640	0.8311	0.8445	0.7291
wCorrel.	0.7604	0.7368	0.8454	0.7837	0.8417	0.8595	0.7359
MAE	0.4489	0.4734	0.3714	0.5539	0.3819	0.3488	0.5156
wMAE	0.3559	0.3743	0.2932	0.5268	0.3017	0.2820	0.4974
RMSE	0.5944	0.6099	0.4788	0.6738	0.4958	0.4547	0.6390
wRMSE	0.4666	0.4857	0.3830	0.6276	0.3933	0.3671	0.6022

 

The ranking, in my opinion, is: 1) FBERA; 2) BERA; 3) FIP; 4) pFIP; 5) SIERA; 6) SBERA; and 7)xFIP.  FBERA easily beats FIP, despite the lack of the FF (fudge factor), and BERA is about even, despite the FF disadvantage.  Since pFIP was designed to predict the next year’s performance with the same factors FIP uses (only dividing by PA instead of IP, now), there’s no surprise it doesn’t match the long-term as well.  SIERA and SBERA are pretty close, but I’ll give the edge to SIERA on the basis of its superior weighted correlation.  SBERA and xFIP are about even in terms of weighted correlation, but SBERA is apparently significantly better at guessing the ERAs of those pitchers with lower IP counts, so it gets the edge.

This next round of comparisons will be on SIERA’s home turf — comparing each pitcher’s stat for one season to their next season’s ERA (with a 40 IP minimum in both seasons… n=2612 season combinations).

	ERA	SIERA	xFIP	FIP	pFIP	BERA	FBERA	SBERA
Correl.	0.325	0.422	0.368	0.365	0.408	0.423	0.381	0.449
MAE	1.081	0.876	0.898	0.935	0.945	0.871	0.933	0.842
wMAE	0.974	0.789	0.801	0.836	0.876	0.778	0.838	0.756
RMSE	1.398	1.137	1.156	1.212	1.179	1.133	1.212	1.098
wRMSE	1.260	1.012	1.027	1.081	1.085	1.006	1.089	0.974

 

For this contest, I’d rank them: 1) SBERA; 2) BERA; 3) SIERA; 4) pFIP; 5) FBERA; 6) xFIP; 7) FIP; and 8) Previous year’s ERA.  Again, I’m penalizing the FF users a little bit, and going with the correlations a bit more.  The fudge factors are less of an advantage when it comes to predicting future years, however, as they’re based on the current year.  I can see an excuse to use fudge factors if your goal is to predict future years.  Really, when it comes strictly to predicting future ERA, the gloves are off, I say (all is fair in love and WAR?).  I’m throwing in past ERAs, past BABIPs, and whatever else I can to see what sticks to the wall (as long as I’m not cheating by introducing information from the future years, of course).  I do have such a model worked out, perhaps for a future article.  But I do see a distinction between an ERA predictor and an ERA estimator in this regard.  Anyway, perhaps I can be convinced to add fudge factors to BERA, by popular demand.

For the next contest, we’ll step into the home field of pFIP, on which Mr. DuPaul showed his formula had a superior correlation (well, correlation squared is what he showed) to the next season’s ERA over SIERA, FIP, and xFIP, when it came to pitchers who’d pitched at least 100 innings in consecutive years between 2007-2012 (n=479).  I’ll be doing the same, only over 2002-2012 (OK, I found another area where I don’t think less is more — this is n=979).

	ERA	SIERA	xFIP	FIP	pFIP	BERA	FBERA	SBERA
Correl.	0.322	0.416	0.408	0.387	0.407	0.414	0.369	0.426
MAE	0.822	0.694	0.696	0.720	0.759	0.675	0.721	0.669
wMAE	0.801	0.678	0.677	0.697	0.776	0.659	0.705	0.659
RMSE	1.032	0.862	0.866	0.902	0.920	0.848	0.913	0.831
wRMSE	1.005	0.838	0.838	0.872	0.936	0.826	0.898	0.815

 

Well, I wasn’t able to confirm pFIP’s superiority here (nor was I for the 2007-2012 seasons), but it did close the gap a bit on SIERA compared with the 40 IP minimum sample.  Well, really, all the FIPs come a lot closer to SIERA (and to BERA and SBERA) at this level of IP.  xFIP is about even with SIERA.  Anyway, perhaps some independent testing is required here to see who’s right about this pFIP vs. SIERA  issue.

Why stop now?  Here’s with a 150 IP minimum (n=631)

	ERA	SIERA	xFIP	FIP	pFIP	BERA	FBERA	SBERA
Correl.	0.329	0.409	0.405	0.404	0.416	0.429	0.399	0.430
MAE	0.751	0.652	0.651	0.657	0.756	0.615	0.654	0.621
wMAE	0.743	0.648	0.646	0.648	0.771	0.610	0.647	0.624
RMSE	0.940	0.802	0.803	0.823	0.904	0.769	0.824	0.763
wRMSE	0.930	0.795	0.793	0.809	0.916	0.760	0.813	0.762

 

OK, now the FIPs have closed the gap on SIERA, though BERA and SBERA are still looking good.  It also looks like BERA has also overtaken SBERA by now.  200 IP minimum is next, with n=211 (last one, I promise):

	ERA	SIERA	xFIP	FIP	pFIP	BERA	FBERA	SBERA
Correl.	0.325	0.417	0.403	0.397	0.432	0.425	0.396	0.431
MAE	0.628	0.612	0.601	0.579	0.849	0.570	0.591	0.639
wMAE	0.627	0.614	0.602	0.578	0.861	0.572	0.590	0.648
RMSE	0.795	0.743	0.725	0.718	0.978	0.697	0.731	0.764
wRMSE	0.793	0.744	0.727	0.716	0.989	0.698	0.730	0.772

 

At this point, I’d say the two left standing are: 1) BERA; and 2) FIP.

How about a graphical representation of the advantage BERA has over SIERA when it comes to IP?  Here’s how often BERA comes closer to the next season’s ERA than SIERA at various IP minimums:

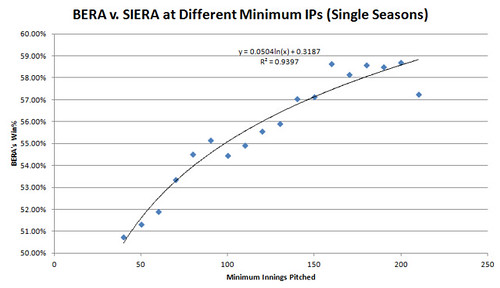
By 230 IP, BERA wins only 53% of the contests, but we’re also talking about a sample of only 27 individual seasons by that point, so I left that and 220 IP out.  Anyway, it’s a very consistent pattern, as you can see, and it’s very much in line with the way BERA also matches up much better directly with ERA than SIERA does in the long-term, as shown in this graph (despite SIERA’s fudge factor advantage):

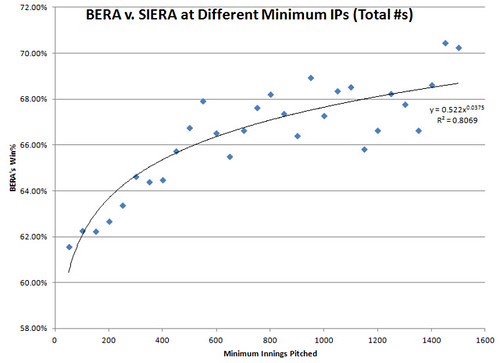
If you’re wondering how FBERA does against SIERA: in the next-season analysis, it starts off at 45.3% at 40 IP, then makes a steady climb and surpasses SIERA by around 140 IP.  At 210 IP, FBERA beats SIERA 60% of the time, and it skyrockets up after that point (but, again, small sample size at that IP level).  FBERA is, of course, better than SIERA in the long run too, but its win percentage stays close to 60% until it suddenly climbs to about 65% with 1500 IP.

SBERA is consistently in the 54-55% range against SIERA for the next season’s ERA, but drops off past a 170 IP cutoff, and is surpassed by about 200 IP.  In the long-term, however, it looks horrible against it, starting around 48% at 50 IP, followed by an incredibly steady decline to about 8% by 1500 IP.

What about how well all these stats relate to the pitchers’ previous ERAs?  Well, I figure that’s a lot less interesting to you fantasy baseballers out there, so here’s just the basics on the 40 IP minimum vs. the last season’s ERA:

	ERA	SIERA	xFIP	FIP	pFIP	BERA	FBERA	SBERA
Correl.	0.323	0.388	0.331	0.320	0.369	0.388	0.355	0.411
MAE	1.088	0.884	0.918	0.965	0.993	0.880	0.945	0.837
RMSE	1.403	1.130	1.168	1.238	1.225	1.129	1.219	1.074

It’s pretty consistent, I think.  A summary of just the RMSEs, to keep this brief (too late for that, I know):

	RMSE vs. Previous Year’s ERA
IP Min	ERA	SIERA	xFIP	FIP	pFIP	BERA	FBERA	SBERA
40	1.403	1.130	1.168	1.238	1.225	1.129	1.219	1.074
100	1.136	0.984	0.985	1.052	1.043	0.975	1.043	0.938
150	1.072	0.923	0.913	0.975	1.017	0.923	0.996	0.882
200	0.972	0.886	0.876	0.919	1.020	0.879	0.958	0.852

About Standard Deviations

In the aforementioned article by Colin Wyers, he points out the relatively low standard deviation of SIERA and says:

Simply producing a lower standard deviation doesn’t make a measure better at predicting future performance in any real sense; it simply makes it less able to measure the distance between good pitching and bad pitching. And having a lower RMSE based upon that lower standard deviation doesn’t provide evidence that skill is being measured. In short, the gains claimed for SIERA are about as imaginary as they can get, and we feel quite comfortable in moving on.

About which, I have to ask: what if the difference between the “true” ERAs for good and bad pitchers isn’t really all that great?  Some food for thought:

 

Perhaps his findings that SIERA came in at a 0.53 weighted standard deviation, whereas FIP’s was 0.83 and ERA’s was 1.71 (I’m not sure these are accurate, by the way… unless I’m misinterpreting what he was finding the standard deviation of), don’t really prove his case.  If the goal of an ERA estimator is to guess the “true” ERA of a pitcher, then perhaps a 0.53 standard deviation is about right, in light of the way ERA’s standard deviation drops with greater IP.  The standard deviation does reach about 0.53 for pitchers with over 1000 IP.  Of course, it should be noted that a lot of pitchers never reach 1000 IP for good reason — they’re not good enough to be given that many IP (well, some were at the tail ends of their careers, too, and their best years weren’t in the sample).  The ERA distribution in my sample:

 

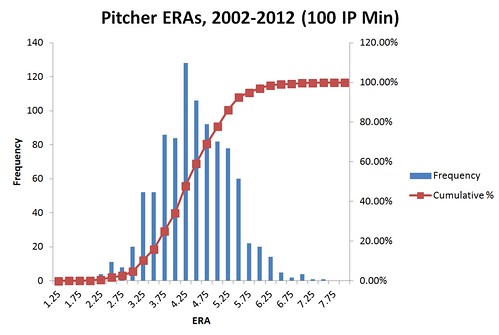
“4.25” is the mode, but you should read that as 4.0 – 4.25.  It’s a pretty close to a normal distribution, but a tiny bit skewed positive (there are more on the high ERA side than a perfectly normal distribution would predict).

Also, let’s consider what the implication of a 0.5 standard deviation would be.  If we say the mean ERA is 4.1, and assume a normal distribution, that would mean about 68.2% of pitchers should have an ERA between 3.6 and 4.6.  13.6% would be between 3.1 and 3.6, with another 13.6% between 4.6 and 5.1.  2.1% would be between 2.6 and 3.1, while another 2.1% would be between 5.1 and 5.6.  The top tenth of a percent would be from 2.1-2.6, and the bottom 0.1% would range between 5.6 and 6.1.  I don’t know about you, but if we’re talking about long-term ERAs for pitchers, that sounds about right to me.  How many pitchers today would you pick to finish their careers with an ERA under 3.1?

Anyway, here are the standard deviations for the different formulas, at various minimum innings cutoffs, and for single seasons:

Min. IP	ERA	SIERA	xFIP	FIP	pFIP	BERA	FBERA	SBERA
40	1.261	0.769	0.702	0.919	0.566	0.765	0.946	0.538
100	0.950	0.638	0.636	0.760	0.470	0.594	0.726	0.381
150	0.848	0.609	0.592	0.701	0.456	0.569	0.686	0.371
200	0.745	0.636	0.614	0.691	0.461	0.557	0.653	0.379

 

Thoughts

I like FBERA, because of its simplicity and the way it confirms my simple BABIP formula’s applicability to ERA estimating.  FBERA’s main weakness is that LD% is something that only stabilizes in the longer-run, which throws off the formula’s usefulness in the shorter term (but it’s still better than FIP in the short term, overall).  Still, despite LD%’s unreliability, it was always useful overall in predicting next season’s ERA, in all the formulas.  I could definitely come up with a formula that used BERA’s factors, but weighted them towards achieving the same goal as FBERA, and it would help alleviate this weakness a bit, at the cost of extra complexity and worse season-to-season prediction.

BERA is something I’m pretty happy with.  It is pretty close to FBERA, only it adds OFFB and Z-Contact%, which help strengthen its season-to-season predictions.  Z-Contact% is something I discovered to be very useful in season-to-season BABIP predictions, as it’s really probably the biggest underlying factor to a pitcher’s popup rate, which is in turn one of the biggest factors in a pitcher’s BABIP.  I could have used GBs instead of OFFBs (it would have been a different, negative weight), but I thought OFFBs made the simplified formula more handy.  It just helps to round out the batted ball profile, for extra consistency.

SBERA is respectable, but it’s arguably kind of an example of what can happen when you try to get too fancy — you lose sight of some important things.  Some of you will disagree with me, I’m sure, but I think that if all of its gains were legitimate, it would be better at predicting things long-term than it is.  I believe it would beat xFIP long-term if it had a fudge factor, but that’s about it.

SIP%  (the percentage of innings pitched as a starter) is a major double-edged sword in my formulas.  I was really resistant to including it, due to my skepticism, but I caved when I saw that it really got results (I mean, it’s a minor factor, but the boost is pretty noticeable).  This was really the main aspect of SIERA that I adopted into my formulas.  My biggest issue with this stat is the major sample bias it introduces.  Relievers with over 40 IP in a season really do have better ERAs (and BABIPs) than starters do.  Relievers with less than 40 IP… not so much.  In individual seasons from 2002-2012, for example, relievers with over 40 IP in relief have an average ERA (IP-weighted) of 3.6; those with less than 40 have an average of 5.2.  I defined “reliever,” by the way, as those with at least twice as many innings in relief as starting.  So, really, does being a reliever make you more effective, or does being an effective reliever make you more likely to pitch 40 or more innings in a season?  I think it’s mainly the latter, but I’m sure there is some innate advantage to being a reliever — you can give more effort per pitch, and the hitters will be less familiar with you.  Oh, and if you’re a closer, you generally don’t have to worry about bad relievers coming in after you and raising your ERA by letting your runners score.  Anyway, it’s a tricky issue to deal with, but I’m inclined to think relievers and starters should be considered separately, and with different formulas (and if the pitcher does both, each role should be considered separately).  I think the inclusion of SIP% makes things a bit sloppy, and really lowers the effectiveness of the formula for both relievers and starters, in order to try to make a compromise.

Oh yeah, also on the topic of SIP%, there’s a -0.53 correlation between it and ERA on a team level; that is, there’s a fairly strong connection between using relievers more and having a higher team ERA.  Of course, I’m sure there’s also a connection between using relievers more and having bad starters…

Getting back a bit to Colin Wyers’ article, he tries to show that with enough innings pitched (at least 400), ERA becomes a better predictor of future ERAs than any of the ERA estimators.  He does this by predicting the 2010 season with 2003-2009 numbers.  Any flags go off for you?  Yes, how reliable is that, really, if you’re putting all your eggs in the basket of 2010?  I confirmed his results, more or less, but it turns out that if you try to predict 2011 with 2003-2009 numbers, BERA and SIERA are both consistently better than just using ERA.  So consider me not sold on that analysis — you’re going to have to do that exercise for more years than just 2010 to be convincing.  It seems entirely possible that 2010 was a fluke year in this regard.  Whatever the case, it is probably fair to say that none of these ERA estimators (or projection systems, judging by Matt Swartz’ article) really give a major edge over just using career ERAs.  So, really, the goal of using them has to be about judging single-season performances, more than anything.

So, as a final note, to sum up: 1) BERA is supposed to show the “true” ERA based on one season’s worth of data; 2) I believe it to be the best formula out there at this role, as far as I’m aware; and, 3) It’s a pretty limiting role — one that incorporates more seasons would be better.  Still, I hope you’ve found all this useful.  Perhaps in a future article, I’ll show you something not held down by the single-season shackles.