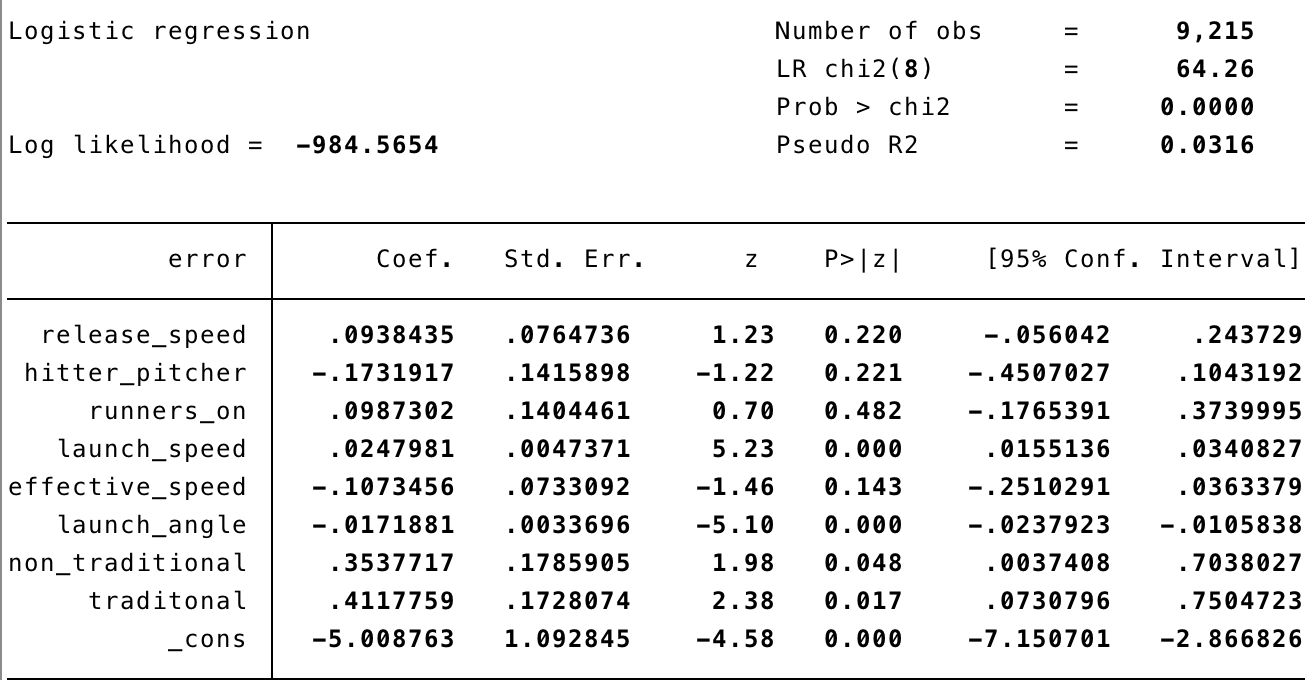
Using Statcast Data to Predict Future Results
Introduction
Using Statcast data, we are able to quantify and analyze baseball in ways that were recently immeasurable and uncertain. In particular, with data points such as Exit Velocity (EV) and Launch Angle (LA) we can determine an offensive player’s true level of production and use this information to predict future performance. By “true level of production,” I am referring to understanding the outcomes a batter should have experienced, based on how he hit the ball throughout the season, rather than the actual outcomes he experienced. As we are now better equipped to understand the roles EV and LA play in the outcome of batted balls, we can use tools like Statcast to better comprehend performance and now have the ability to better predict future results.
Batted Ball Outcomes
Having read several related posts and projection models, particularly Andrew Perpetua’s xStats and Baseball Info Solutions Defense-Independent Batting Statistic (DIBS), I sought to visualize the effect that EV and LA had on batted balls. For those unfamiliar with the Statcast measurements, EV is represented in MPH off the bat, while LA represents the trajectory of the batted ball in Vertical Degrees (°) with 0° being parallel to the ground.
The following graph visualizes how EV and LA together can visually explain batted ball outcomes and allows us to identify pockets and trends among different ball in play (BIP) types.

The following two density graphs were created to show the density of batted ball outcomes by EV and LA, without the influence of one another.


As expected, our peaks in density are located where we notice pockets in Graph 1. Whereas home runs tend to peak at 105 MPH and roughly 25°, we see that outs and singles are more evenly distributed throughout and doubles and triples fall somewhere in between, with peaks around 100 MPH and 19°. These graphs served as a substantiation to the understanding that hitting the ball hard and in the air correlates to a higher likelihood of extra-base hits. I found it particularly interesting to see triples resembled doubles more than any other batted-ball outcome in regards to EV and LA densities. Triples are often the byproduct of a variable such as larger outfields, defensive misplays, and batter sprint speed, which are three factors not taken into account during this project.
Expected Results
My original objective in this project was to create a table of expected production for the 2017 season using data from 2017 BIP. Through trial and error, I shifted my focus towards the idea that I could use this methodology to better understand the influence expected stats using EV/LA can have in predicting future results. With the implementation of Statcast in all 30 Major League ballparks beginning in 2015, I gathered data on all BIP from 2015 and 2016 from Baseball Savant’s Statcast search database. In addition, I created customized batting tables on FanGraphs for individual seasons in 2015, 2016, and 2017 for all players with a plate appearance (PA).
After cleaning the abundance of Statcast data that I had downloaded, I assigned values of 0 and 1 to all BIP, representing No Hit or Hit respectively, and values of 1, 2, 3, and 4 for Single/ Double/Triple/Home Run respectively. Comparing hits and total bases to their FanGraphs statistics for all individuals, I made sure all BIP were accounted for and their real-life counting statistics matched. Following this, I created a table of EV and LA buckets of 3 MPH and 3°, along with bat side (L/R), and landing location of the batted ball (Pull, Middle, Opposite), using Bill Petti’s horizontal spray angle equation. While projection tools often take into account age, park factors, and other variables, my intention was to find the impact of my four data points and to tell how much information this newly quantifiable batted-ball data can give us.
By calculating Batting Average (BA) and Slugging Percentage (SLG) for every bucket, we can more accurately represent a player’s true production by substituting in these averages for the actual outcomes of similar batted balls. For instance, a ball hit the opposite way by a RHB in 2015 and 2016 between 102 and 105 MPH and 21° and 24° was worth .878 BA and a 2.624 SLG, representing the values I will substitute for any batted ball hit in this bucket.
While a player’s skills may be unchanged, opportunity in one season can be tremendously different from the following, affecting individual counting statistics. With a wide range of factors that can lead to changes in playing time, from injuries to trades to position battles, rate statistics are steadier when looking at year-to-year correlation than counting statistics. Typically rate statistics, such as BA and SLG, will correlate better because they remove themselves from the variability and uncertainty of playing time, which counting statistics are predicated heavily on. Totaling the BA and SLG for each individual batter’s BIP from the 2015 and 2016 season, I was able to then divide by their respective at-bats for that year to determine their expected BA (xBA) and SLG (xSLG).
Year-to-Year Correlation Rates For BA/SLG/xBA/xSLG to Next Season BA/SLG, 2015 to 2016 / 2016 to 2017
|
Season (Min. 200 AB Per Season) |
||
|
Statistic |
2015 to 2016 |
2016 to 2017 |
|
BA |
0.140 |
0.173 |
|
xBA |
0.163 |
0.179 |
|
SLG |
0.244 |
0.167 |
|
xSLG |
0.301 |
0.204 |
While our correlation rates for xBA and xSLG are not terribly strong from season to season over their BA and SLG counterparts, we are seeing some positive steps towards predicting future performance. The thing that stands out here is the decline in SLG and xSLG from 2015/2016 to 2016/2017 and my suspicions are that batters are beginning to use Statcast data. It is widely known that a “fly-ball revolution” has been taking place and many players are embracing this by changing their swings and trying to elevate and drive the ball more than ever. With a new record in MLB home runs in 2017, I would not be surprised to see our correlation rates jump back up next season as the trend has now been identified and our batted-ball data should reflect that.
By turning singles, doubles, triples, and home runs into rate statistics per BIP, we are able to put aside the playing time variables and apply these rates to actual opportunities. Similar to calculating xBA and xSLG, I created a matrix of expected BIP rates (xBIP%) for each possible BIP outcome (x1B%, x2B%, x3B%, xHR%, xOut%). In other words, for each bucket of EV/LA/Stand/Location, I calculated the percentage of all batted-ball outcomes that occurred in that bucket (i.e. 99-102 MPH/18-21°/RHB/Middle: x1B% = 0.012, x2B% = 0.373, x3B% = 0.069, xHR% = .007, xOut% = .536), and summed the outcomes for each batter, giving their expected batting line for that season.
Using this information, I wanted to find the actual and expected rates per BIP for each possible outcome (actual = 1B/BIP, expected = x1B/BIP, etc.) and apply these to the next seasons BIP totals. For example, by taking the 2B/BIP and x2B/BIP for 2015 and multiplying by 2016BIP, I can find the correlation rates for actual and expected results, with disregard to opportunity and playing time in either season. Below are the correlations from 2015 to 2016 and 2016 to 2017, with both their actual and expected rates applied to the BIP from the following season.
Correlation Rates For Actual and Expected Batted Ball Outcomes, 2015 to 2016 /
2016 to 2017
|
Season (200 BIP Per Season) |
||
|
Statistic |
2015 to 2016 |
2016 to 2017 |
|
1B |
0.851 |
0.843 |
|
x1B |
0.871 |
0.865 |
|
2B |
0.559 |
0.594 |
|
x2B |
0.624 |
0.644 |
|
3B |
0.173 |
0.262 |
|
x3B |
0.107 |
0.098 |
|
HR |
0.628 |
0.608 |
|
xHR |
0.662 |
0.617 |
Looking at the above table, the expected statistics have a higher correlation to the following seasons production than a player’s actual stats. The lone area where actual stats prevail in our year-to-year correlations is projecting triples, which should come as no surprise. Two noticeable areas that this study neglects to take into account are park factors and batter sprint speed. Triples, more than any other batted-ball outcome, rely on these two factors, as expansive power alleys and elite speed can influence doubles becoming triples very easily.
One interesting area where this projection tool flourishes is x2B/BIP to home runs in the following season. By taking the x2B/BIP and multiplying by the following seasons’ BIP and then running a correlation to the home runs in that second season, we see a tremendous jump from the actual rate in season one to the expected rate in season one.
Correlation Rates of 2B/x2B To HR In Following Season, 2015 to 2016 / 2016 to 2017
|
Season (200 BIP Per Season) |
||
|
Statistic |
2015 to 2016 |
2016 to 2017 |
|
2B -> HR |
0.381 |
0.322 |
|
x2B -> HR |
0.535 |
0.420 |
Conclusion
With this information, we can continue to understand the underlying skills and more accurately determine expected future offensive production. By continuing to add variables to tools like this, including age, speed, park factors, as many projection models have done, we can incrementally gain a better understanding to the question at hand. This research attempted to show the effect EV/LA/Stand/Location have on batted balls and how that data can help us find tendencies, underlying skills, and namely, competitive advantages.
Having strong correlation rates on xBIP% to the next season’s actual results, it is exciting to find another area of baseball that gives the information and ability to better understand players and their abilities. With the use of Statcast, we are looking to create a better comprehension of what has happened and how can we use that to know what will happen, and it appears that we have.